第二章 线搜索技术

Posted 2021-06-29 是璇子鸭

内容来自马昌凤编著的《最优化方法及其Matlab程序设计》，文章仅为个人的学习笔记，感兴趣的朋友详见原书

精确线搜索&非精确线搜索

精确线搜索及其Matlab实现

基本思想：首先确定包含问题最优解的搜索区间，然后采用某种插值或分割技术缩小这个区间，进行搜素求解。

分类：一类是使用导数的搜索，如插值法、牛顿法及抛物线法等；
另一类是不用导数的搜索，如0.618法、分数法及成功-失败法等

黄金分割法（0.618法）

算法：

程序：

function [s,phis,k,G,E]=golds(phi,a,b,delta,epsilon)
%功能: 0.618法精确线搜索
%输入: phi是目标函数, a, b 是搜索区间的两个端点
%         delta, epsilon分别是自变量和函数值的容许误差
%输出:  s, phis分别是近似极小点和极小值,  G是nx4矩阵,
%         其第k行分别是a,p,q,b的第k次迭代值[ak,pk,qk,bk],
%          E=[ds,dphi], 分别是s和phis的误差限.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
t=(sqrt(5)-1)/2;  h=b-a;  phia=feval(phi,a); phib=feval(phi,b);
p=a+(1-t)*h;  q=a+t*h; phip=feval(phi,p); phiq=feval(phi,q);
k=1;  G(k,:)=[a, p, q, b]; 
while(abs(phib-phia)>epsilon)|(h>delta)
    if(phip<phiq)
        b=q;  phib=phiq; q=p; phiq=phip;
        h=b-a; p=a+(1-t)*h;  phip=feval(phi,p);
    else
        a=p; phia=phip;  p=q; phip=phiq;
        h=b-a;  q=a+t*h;  phiq=feval(phi,q);
    end
    k=k+1;  G(k,:)=[a, p, q, b]; 
end
ds=abs(b-a); dphi=abs(phib-phia);
if(phip<=phiq)
    s=p;  phis=phip;
else
    s=q;  phis=phiq;
end
E=[ds,dphi];

非精确线搜索及其Matlab实现

Wolf准则

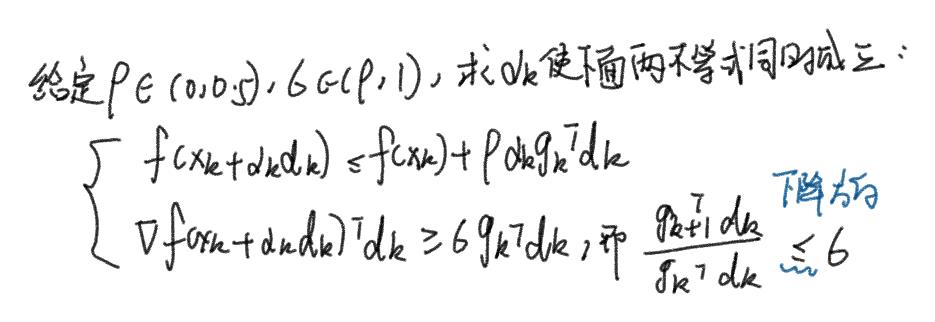
Armijo准则

算法：

程序：

function mk=armijo(xk,dk )
beta=0.5;  sigma=0.2;
m=0; mmax=20;
while (m<=mmax)
    if(fun(xk+beta^m*dk)<=fun(xk)+sigma*beta^m*gfun(xk)'*dk)
        mk=m;  break;
    end
    m=m+1;
end
alpha=beta^mk
newxk=xk+alpha*dk
fk=fun(xk)
newfk=fun(newxk)

说明：此处的$fun$和$gfun$分别指目标函数和它的梯度函数的子程序，执行时这两个子程序需在armijo运行前准备好。