8.6 归纳式迁移学习
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了8.6 归纳式迁移学习相关的知识,希望对你有一定的参考价值。
5.1、归纳式迁移学习
基于 Boosting,提出了基于实例的TrAdaBoost 迁移学习算法.当目标域中的样本被错误地分类之后,可以认为这个样本是很难分类的,因此增大这个样本的权重,在下一次的训练中这个样本所占的比重变大.如果源域中的一个样本被错误地分类了,可以认为这个样本对于目标数据是不同的,因此降低这个样本的权重,降低这个样本在分类器中所占的比重.
深度神经网络可以学习可迁移的特征,这些特征可以很好地泛化到新的任务中,从而实现域适应。然而,随着深度特征最终沿网络由一般特征向特定特征的转变,在更高的层次上特征的可迁移性显著下降,因为源数据与目标数据之间的分布差距,域差异增大。因此,减少数据集偏差和增强任务特定层的可移植性是很重要的。
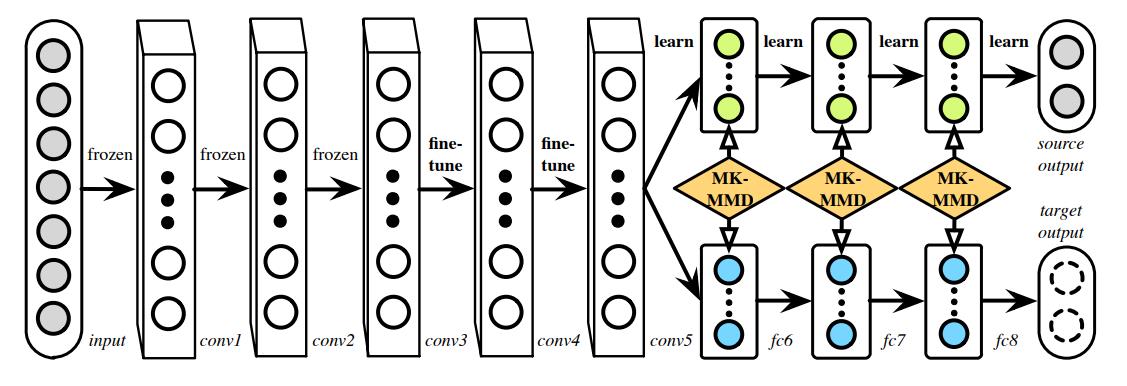
为了解决迁移学习中的域适应问题,Long Mingsheng 基于 DDC( Deep Domain Confusion,深度领域适配) 提出深度适配网络 DAN( Deep Adaptation Network) 1.DDC 是在预训练的 AlexNet 网络的第 7层加入了 MMD距离 来减小 D S D_S DS 和 D T D_T DT 之间的差异. DAN 是深度迁移学习方法,它适配高层网络DDC,并加入了多核的 MMD( MK-MMD) .MMD 是把源域和目标域用一个相同的映射,映射到一个再生核希尔伯特空间( RKHS) 中,然后求映射后两部分数据的均值差异,就当作是两部分数据的差异.在 MMD中核是固定的,可以选择是高斯核或者线性核.MK-MMD 提出用多个核去构造这个总的核,这样效果比一个核更好.
DDC请看: DDC——Deep Domain Confusion Maximizing for Domain Invariance_
它很好地解决了 DDC 的两个问题:
- 一 是 DDC 只适配了一层网络,而 DAN 适配最后三层( 6~8 层) 如图5-1,网络的迁移能力在最后三层开始就会变得专化( specific) ,所以要重点适配这三层.
- 二 是 DDC 是用了单一核的 MMD,单一固定的核可能不是最优的核.DAN 用了多核的 MMD( MK-MMD) ,效果比 DDC 更好.
DAN
图
5
−
1
图5-1
图5−1
MK-MMD
定义:源域和目标域分布分别用概率
p
p
p和
q
q
q表示。
H
k
\\mathcal{H}_{k}
Hk 表示具有特征核
k
k
k的希尔伯特空间(RKHS)。分布
p
p
p在
H
k
\\mathcal{H}_{k}
Hk中的平均嵌入是
μ
k
(
p
)
\\mu_{k}(p)
μk(p),则均方差为
E
x
∼
p
f
(
x
)
=
⟨
f
(
x
)
,
μ
k
(
p
)
⟩
H
k
\\mathbf{E}_{\\mathbf{x} \\sim p} f(\\mathbf{x})=\\left\\langle f(\\mathbf{x}), \\mu_{k}(p)\\right\\rangle_{\\mathcal{H}_{k}}
Ex∼pf(x)=⟨f(x),μk(p)⟩Hk ,其中
f
∈
H
k
f \\in \\mathcal{H}_{k}
f∈Hk。概率分布
p
p
p和
q
q
q之间的MK-MMD
d
k
(
p
,
q
)
d_{k}(p, q)
dk(p,q)被定义为
p
p
p和
q
q
q的平均嵌入均方差之间的希尔伯特空间距离。
d
k
2
(
p
,
q
)
≜
∥
E
p
[
ϕ
(
x
s
)
]
−
E
q
[
ϕ
(
x
t
)
]
∥
H
k
2
(5.1-1)
d_{k}^{2}(p, q) \\triangleq\\left\\|\\mathbf{E}_{p}\\left[\\phi\\left(\\mathbf{x}^{s}\\right)\\right]-\\mathbf{E}_{q}\\left[\\phi\\left(\\mathbf{x}^{t}\\right)\\right]\\right\\|_{\\mathcal{H}_{k}}^{2}\\tag{5.1-1}
dk2(p,q)≜∥∥Ep[ϕ(xs)]−Eq[ϕ(xt)]∥∥Hk2(5.1-1)
如果
d
k
2
(
p
,
q
)
=
0
d_{k}^{2}(p, q)=0
dk2(p,q)=0 则
p
=
q
p=q
p=q。
特征核
k
k
k 为
k
(
x
s
,
x
t
)
=
⟨
ϕ
(
x
s
)
,
ϕ
(
x
t
)
⟩
k\\left(\\mathbf{x}^{s}, \\mathbf{x}^{t}\\right)=\\left\\langle\\phi\\left(\\mathbf{x}^{s}\\right), \\phi\\left(\\mathbf{x}^{t}\\right)\\right\\rangle
k(xs,xt)=⟨ϕ(xs),ϕ(xt)⟩,被定义为m的凸组合PSD核
{
k
u
}
\\left\\{k_{u}\\right\\}
{ku}
K
≜
{
k
=
∑
u
=
1
m
β
u
k
u
:
∑
u
=
1
m
β
u
=
1
,
β
u
⩾
0
,
∀
u
}
,
(5.1-2)
\\mathcal{K} \\triangleq\\left\\{k=\\sum_{u=1}^{m} \\beta_{u} k_{u}: \\sum_{u=1}^{m} \\beta_{u}=1, \\beta_{u} \\geqslant 0, \\forall u\\right\\},\\tag{5.1-2}
K≜{k=u=1∑mβuku:u=1∑mβu=1,βu⩾0,∀u},(5.1-2)
约束系数
{
β
u
}
\\left\\{\\beta_{u}\\right\\}
{βu} 的实施保证了多核 k是特点。
DAN网络结构
由5个卷积层
(
con
v
1
−
con
v
5
)
(\\operatorname{con} v 1-\\operatorname{con} v 5)
(conv1−conv5) 和3个全连接层(
(
f
c
6
−
(f c 6-
(fc6−
f
c
8
)
.
f c 8) .
fc8). 每个
f
c
f c
fc 层
ℓ
\\ell
ℓ 学习非线性映射
h
i
ℓ
=
\\mathbf{h}_{i}^{\\ell}=
hiℓ=
f
ℓ
(
W
ℓ
h
i
ℓ
−
1
+
b
ℓ
)
f^{\\ell}\\left(\\mathbf{W}^{\\ell} \\mathbf{h}_{i}^{\\ell-1}+\\mathbf{b}^{\\ell}\\right)
fℓ(Wℓhiℓ−1+bℓ),
h
i
ℓ
\\mathbf{h}_{i}^{\\ell}
hiℓ 是点
x
i
\\mathbf{x}_{i}
xi的隐藏特征。
f
ℓ
f^{\\ell}
fℓ 是激活函数, 隐藏层时为
f
ℓ
(
x
)
=
max
(
0
,
x
)
f^{\\ell}(\\mathbf{x})=\\max (\\mathbf{0}, \\mathbf{x})
fℓ(x)=max(0,x),输出层时为
f
ℓ
(
x
)
=
e
x
/
∑
j
=
1
∣
x
∣
以上是关于8.6 归纳式迁移学习的主要内容,如果未能解决你的问题,请参考以下文章