8.7 Meta learning元学习全面理解MAMLReptile

Posted 2021-06-29 炫云云

文章目录

• • 1、介绍
  • • few-shot learning
    • reinforcement learning
  • 2、概念
  • 3、 Meta learning 三个步骤
  • • 定义一组learning algorithm
    • 损失函数
    • 寻找最好的F
  • 4、元学习过程总结
  • • 元学习task定义
  • 5、Meta Learning实例：Omniglot
  • • N-way K-shot
  • 6、MAML
  • • 目标函数
    • MAML vs transfer learning
    • MAML的训练
    • MAML Toy Example
    • 算法
    • 梯度数学推导
    • 真正的实现
    • MAML 应用：Translation
  • 7、Reptile
  • • 梯度更新过程
    • • 训练过程
  • 8、More about Meta Learning
  • 参考资料

1、介绍

元学习Meta learning = 学习如何去学习Learn to learn

元学习是对模型的一种研究与学习。相对于deep learning在一个task（任务）中通过对样本的学习以对新样本做出判断，元学习的目标可以看做是将task视作样本，通过对多个task的学习，以使元模型（meta-learner）能够对新的task做出快速而准确的学习。

和Life-long方法有所不一样：

方法	区别
Life-long	one model for all the tasks
Meta	How to learn a new model

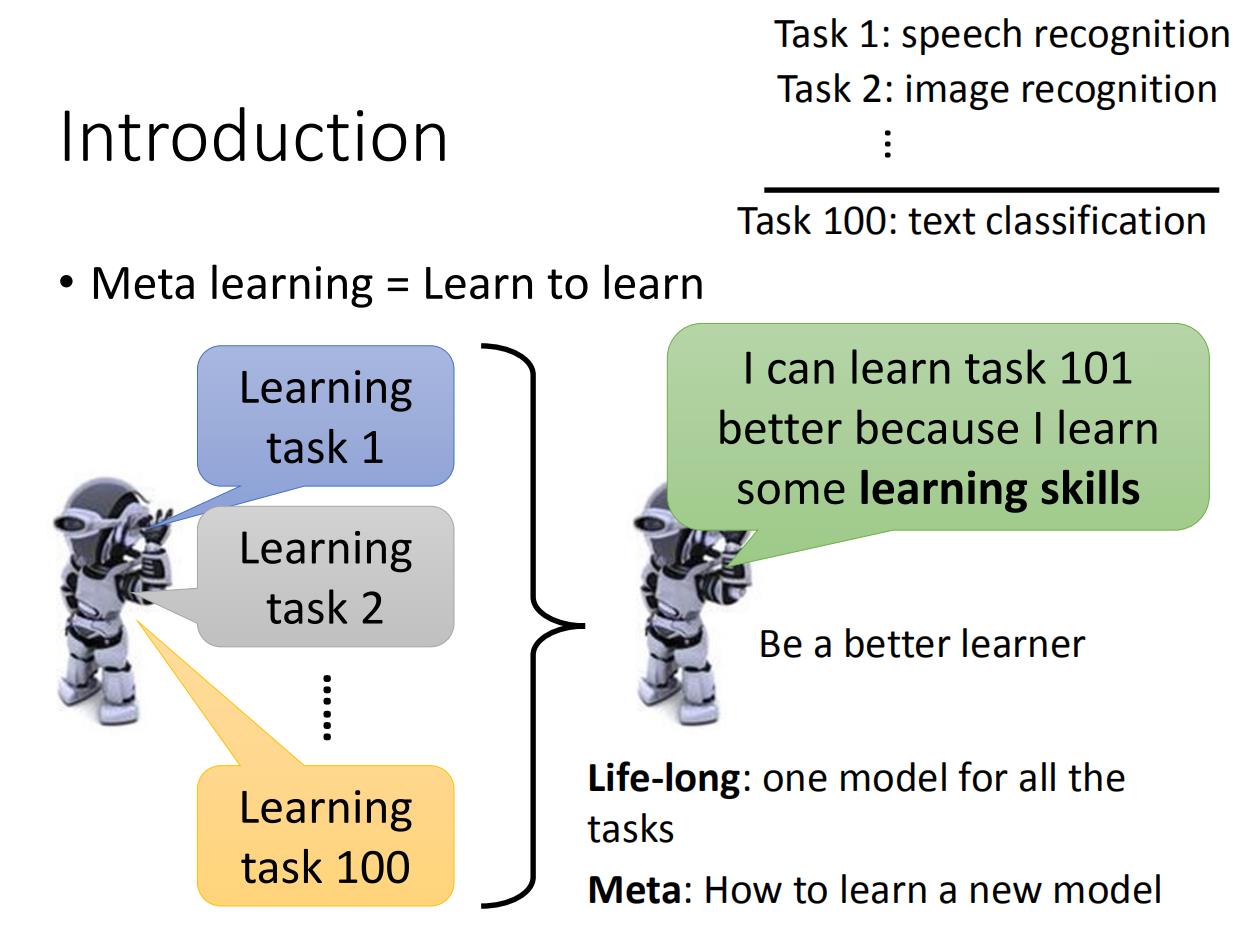
举个例子就是，机器之前学习了100个task，之后机器学习第101个task的时候，会因为之前学习的100个task所具有的学习能力，而让第101个task表现得更好。比如说第一个任务是语音识别，第二个任务是图像识别，第一百个任务是文本分类，机器会因为之前所学到得任务，所以在后面得任务学习得更好。

这个和life long learning有什么区别吗！好像很像诶。确实，life long learning和meta learning都是要根据以往的task，希望对现在的task有所帮助，但是meta learn所要求的是学习新的task时候有新的model（训练后的），但是life long learning始终是一个模型。

few-shot learning

few-shot learning——小样本学习，是指通过极少的样本学习获得（监督/非监督）回归、分类模型。在现有的研究成果中，小样本学习可以基于fine-tune、metric(如孪生网络)、基于meta-learning等。在基于meta-learning的少样本学习中，已有memory-augmented neural networks (Santoro et al., 2016)、meta-learner LSTM (Ravi & Larochelle, 2017)等经典学习方法。

小样本学习一直和元学习系紧密。元学习的目标就是通过学习大量的task ，从而学习到内在的元知识，从而能够快速的处理新的同类任务，这和少样本学习的目标设定是一样的。我们也希望通过很多task来学习识别物体这种能力，从而面向新的少样本学习任务，我们能够充分利用我们已经学习到的识别能力（也就是元知识），来快速实现对新物体的识别。而在这里，通过前面的分析，我们明白了，我们要研究如何通过元学习的方式来让神经网络学会比较这个元知识能力。

reinforcement learning

相比于深度学习，强化学习的训练样本没有标签，是通过环境与决策的奖惩政策来进行学习。强化学习的过程是动态的，强调与环境进行交互，其优势在于解决决策问题，如推荐系统等。在本文中，MAML不仅可适用于few-shot learning，也同样适用于强化学习。

2、概念

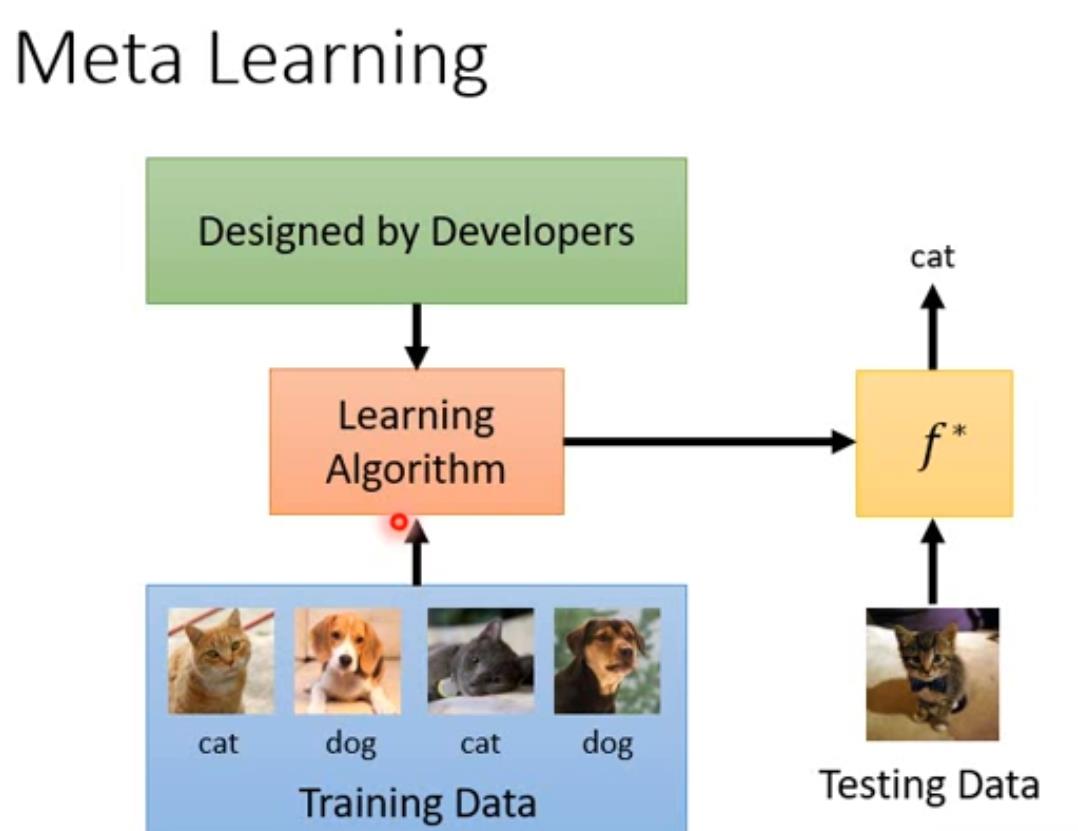
机器学习：用Training Data训练由我们设计的Learning Algorithm，得到一个最优算法$f^{\ast }$ ，可以用来完成相应的任务（猫狗识别）

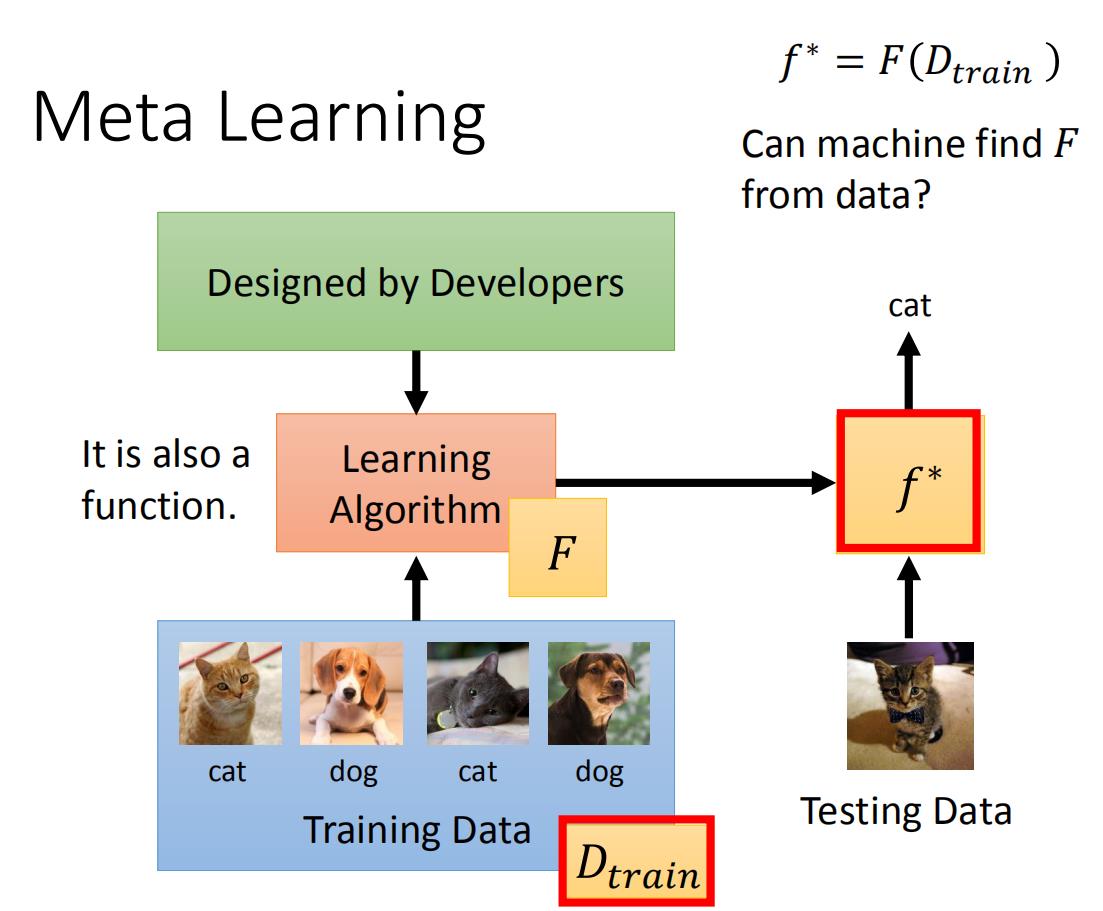
meta learning方法是：依旧给模型很多训练数据，我们将Learning Algorithm当作是一个F（function），我们需要$F$做的事生成另一个$f^{\ast }$（function），而这个f可以用来做影像识别。我们meta learning的方法就是找到$F$。

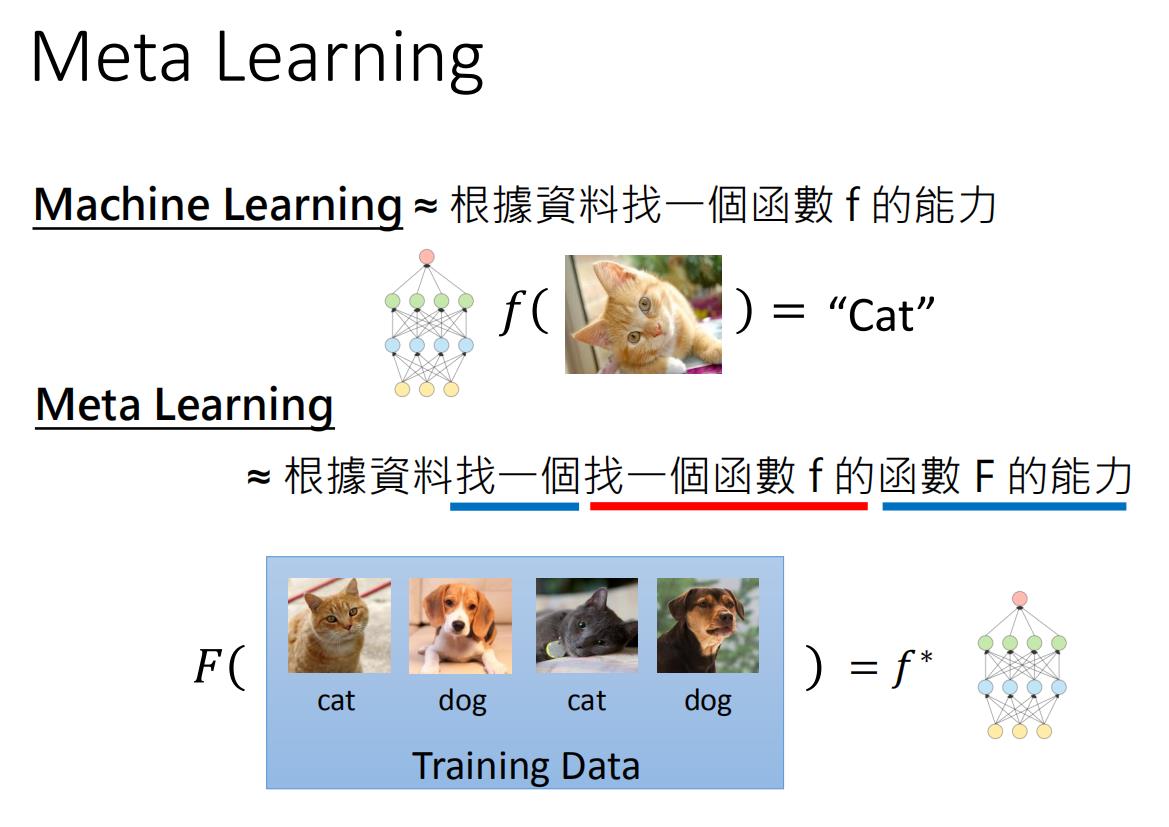
Machine Learning ≈ 根据数据找一个函数 f 的能力

meta learning：用$D_{train}$ 训练由我们设计的F，得到一个完成相应任务的$f^{\ast }$函数 ，怎么感觉和上面没什么区别？

其实不一样，Meta Learning≈ 根据数据找一个找一个函数 f 的函数 F 的能力。$F$的输入是训练数据，输出是解决一个小问题的f,即
$$f^{\ast }=F\left(D_{\text{train }}\right)$$

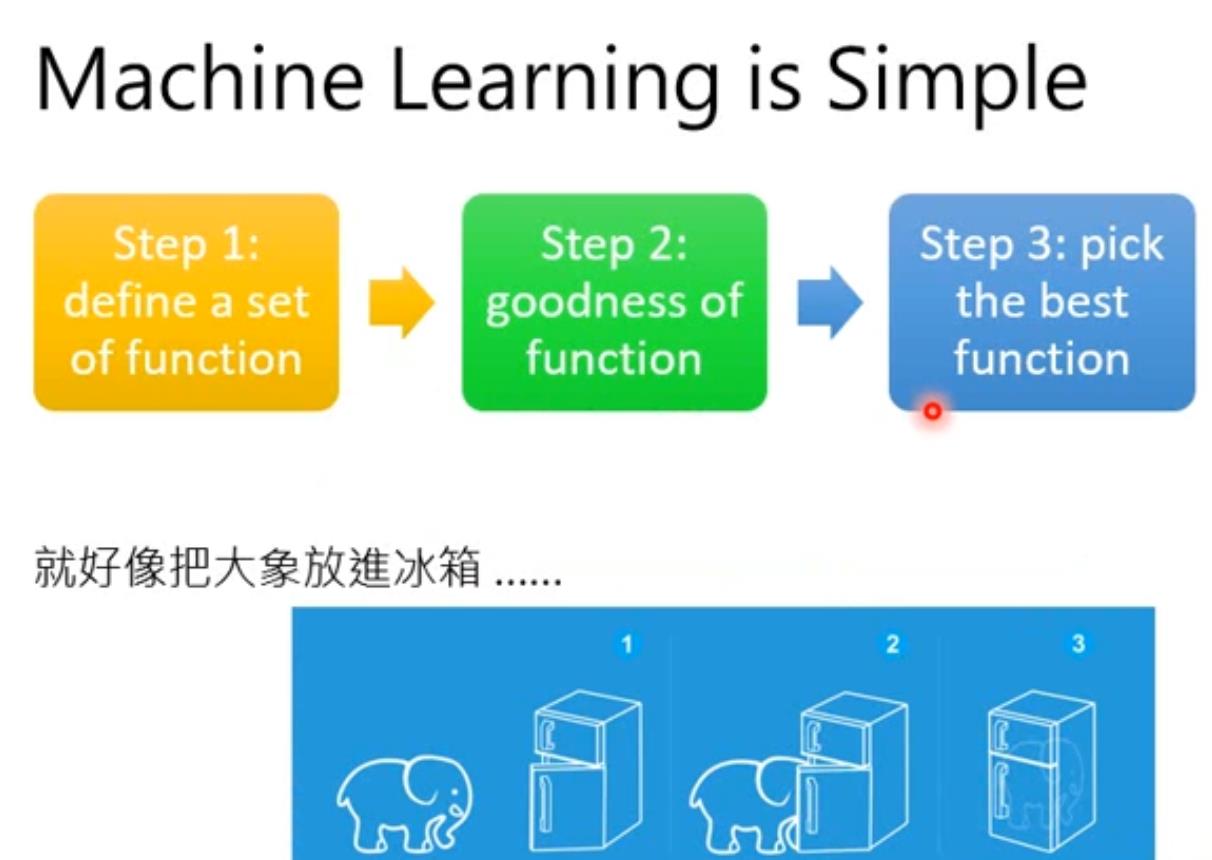
机器学习中是知道函数$f$，而是训练函数f的参数；机器学习的方法可以简单理解为三步：

1. 定义一个function 集合

2. 找到一个$f$好坏的度量指标（loss function）

3. 在这个集合中寻找最好的$f$

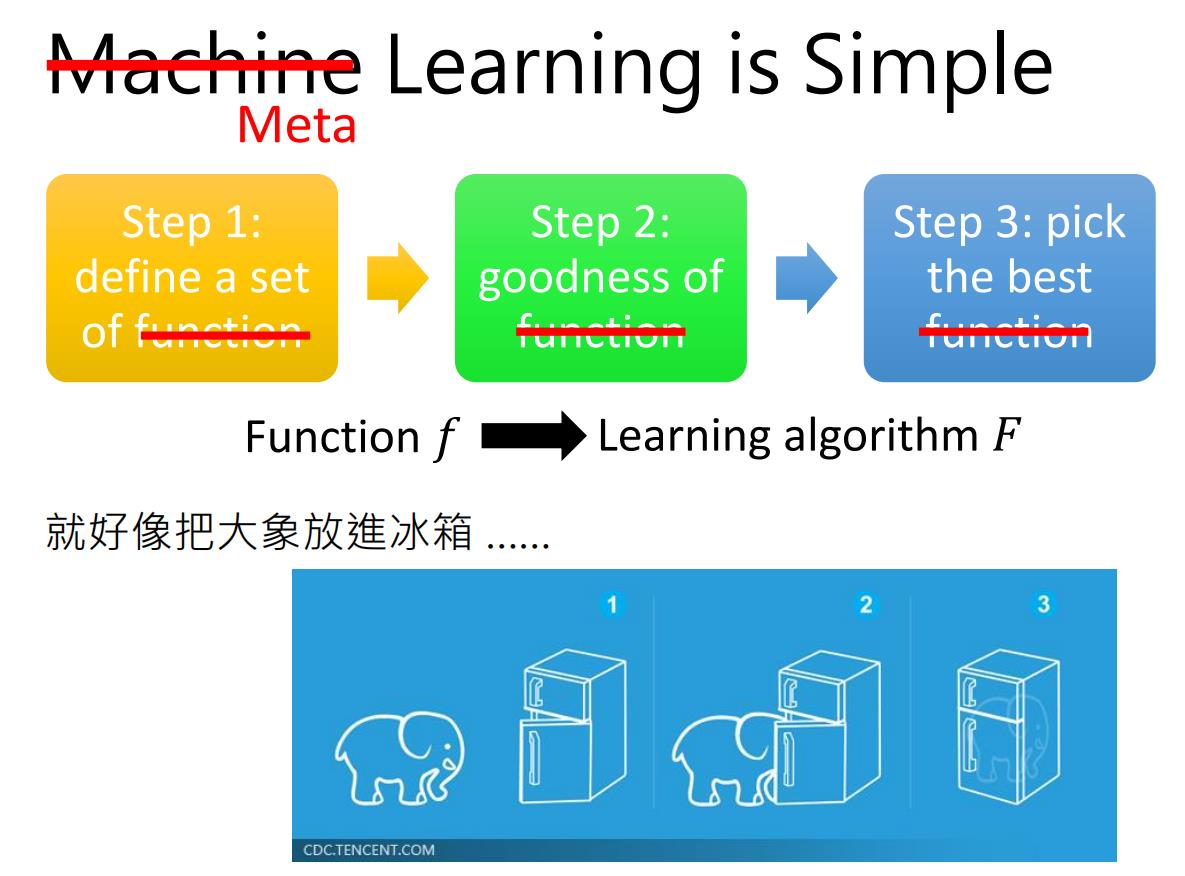
元学习是不知道函数$f$，而是训练函数F找到$f$（含参数）。

我们meta learning的方法和machine learning的方法是十分相似的，也是三步：

1. 定义一组learning algorithm $F$的集合，

2. 定义一个判别learning algorithm 好坏的方法

3. 找一个最好的learning algorithm做为$F$。

3、 Meta learning 三个步骤

定义一组learning algorithm

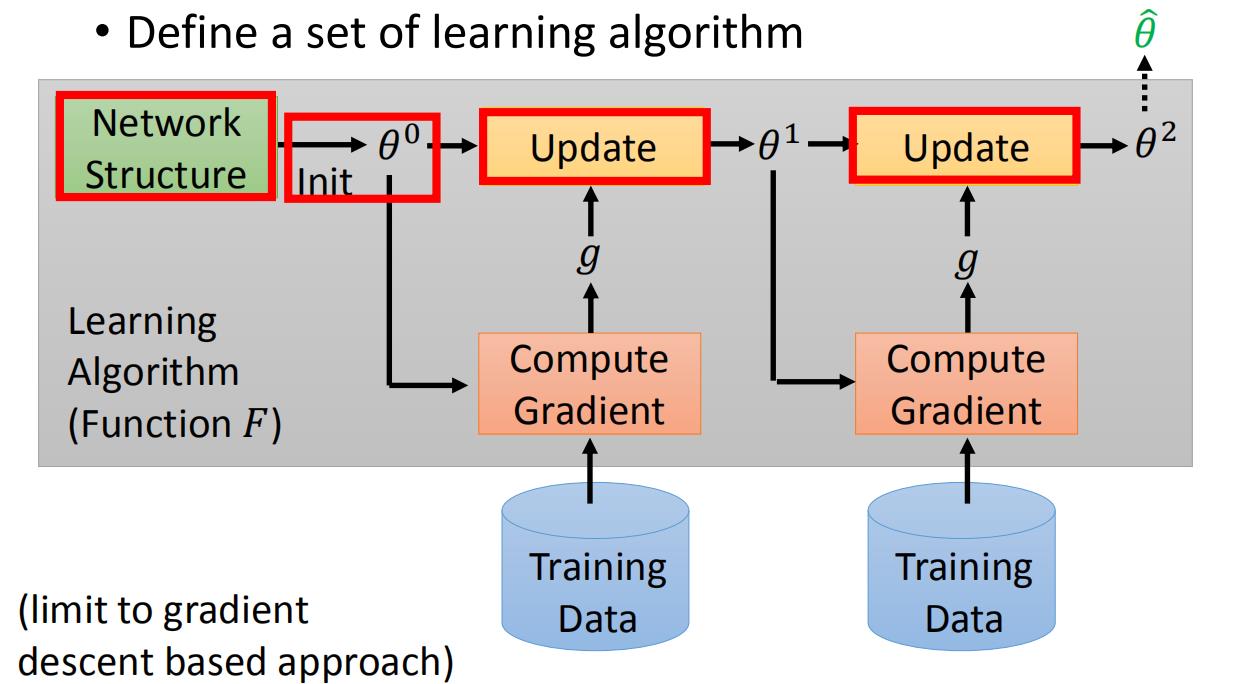
首先，看看如何设置一个learning algorithm set。先来看机器学习中是如何进行learning algorithm的。以基于GD优化的算法为例，先是定义了一个神经网络结构，之后初始化参数值，之后根据训练数据计算梯度，更新参数，图中的每一步的gradient $g$其实不一样，最后得到最优的参数。

红色的格子都是人为设定的，网络结构的选择，参数的初始化，参数更新的方法，都是人为设计的，红框中如果我们定义不同的东西，实际上就是不同的算法。

那么这些部分能否是机器自己设计呢！我们参数的初始值能不能让机器自己初始化呢！假设机器自己初始化参数，机器自己选择更新方法，机器自己选择神经网络结构，这就是我们meta learning的learning algorithm set。

损失函数

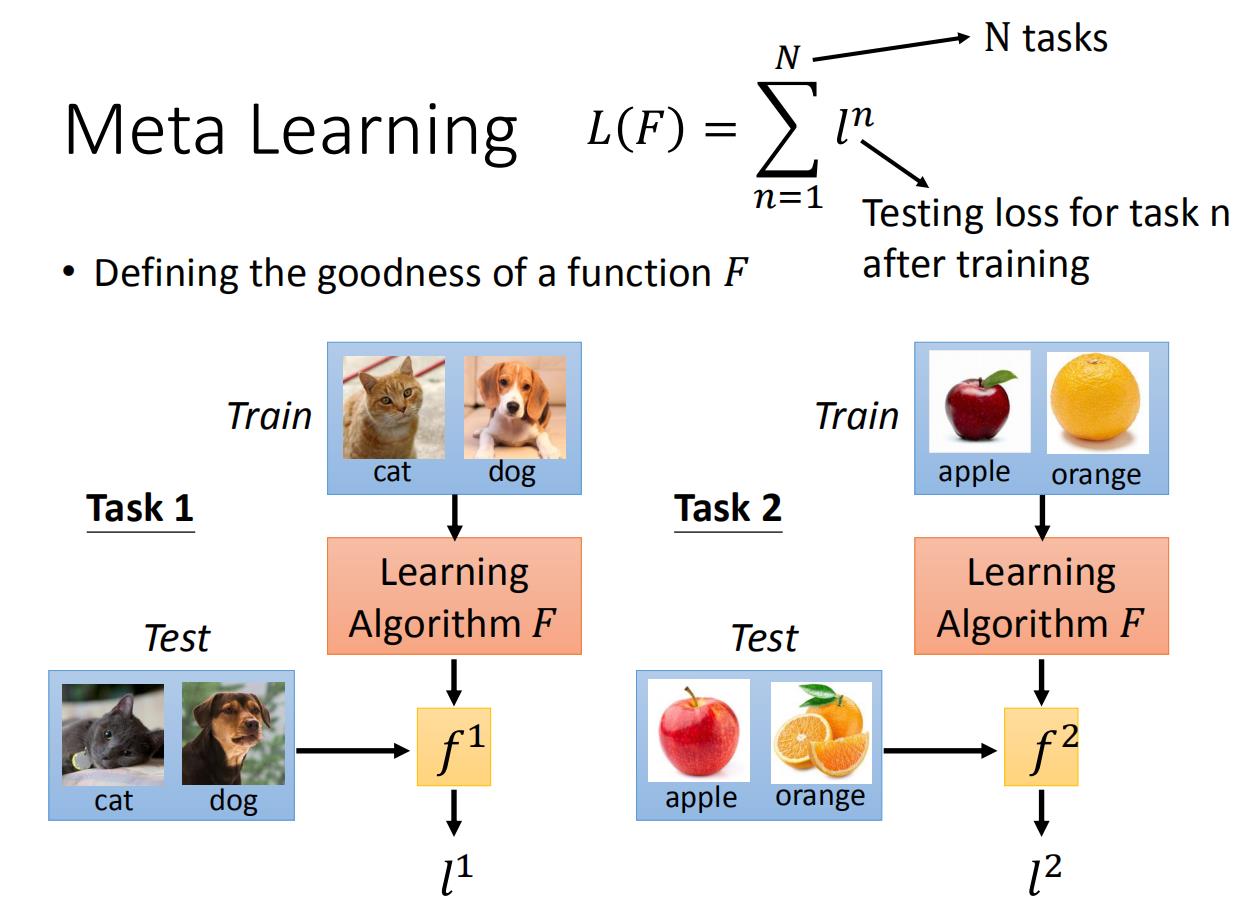
这个过程的损失函数：比如我们用一个learning algorithm $F$。首先用$F$进行猫狗分类器的学习，之后得到了一个$f^1$，$f^1$的训练数据进行测评，得到$f^1$的loss function $l^1$。之后再用F进行苹果橘子分类器的学习，得到一个$f^2$，$f^2$的训练数据进行测评，得到$f^2$的loss function $l^2$。

这里用$F$完成n个分类task，之后对每一个task求一个$l$。之后我们把所有的$l$都加在一起，就变成了我们最后的损失函数$L(F)$。我们就是使用$L(F)$来评估F的。

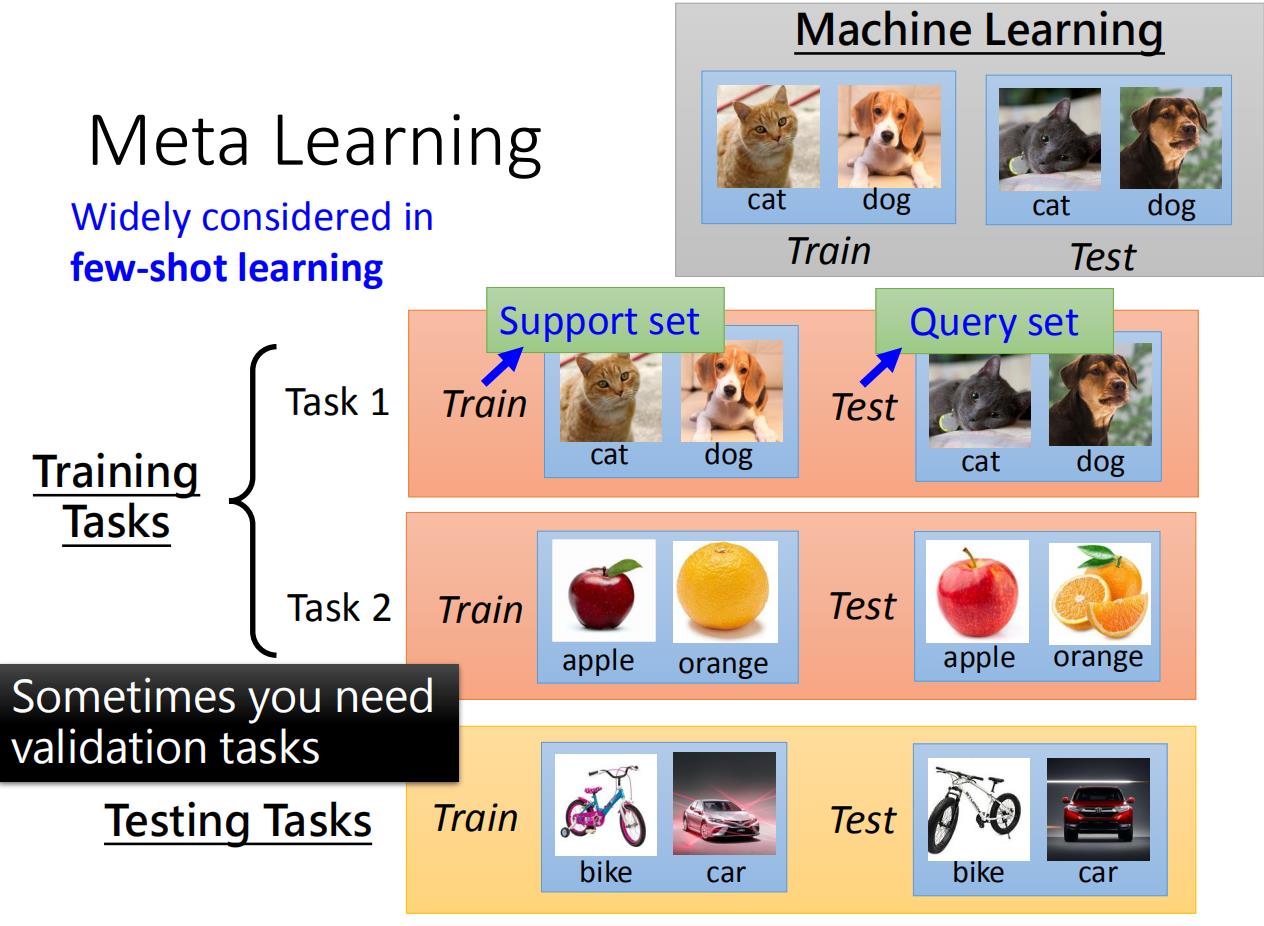
从这里可以看到机器学习和元学习在数据上不一样。一般的机器学习任务是单任务的，所以数据集是一堆训练数据，和测试数据。但是在meta learning的任务是多任务的，所以在这种情况下，我们需要做的是将很多的任务分为训练任务和测试任务，之后每一个小的任务都有训练数据和测试数据。比如说一共有十个任务，我们将其中的八个作为是训练任务，剩余的两个作为测试任务，其中每一个任务都有自己的测试数据和训练数据。以此来检测meta learning的学习能力。

这里要说明：

1. 由于元学习有多个任务，每个任务如果有很多数据，那么训练时间会很长很长，因此，元学习中每个任务的数据不会很多，所以元学习也叫few-shot learning，为了和机器学习区分开，训练和测试数据分别叫Support set和Query set。
2. 和机器学习一样，当我们的元学习中的训练任务很多的时候，我们可以将其中一部分切出来作为验证任务：validation tasks。
3. 元学习中的testing task可以和training task一样，也可以不一样。

寻找最好的F

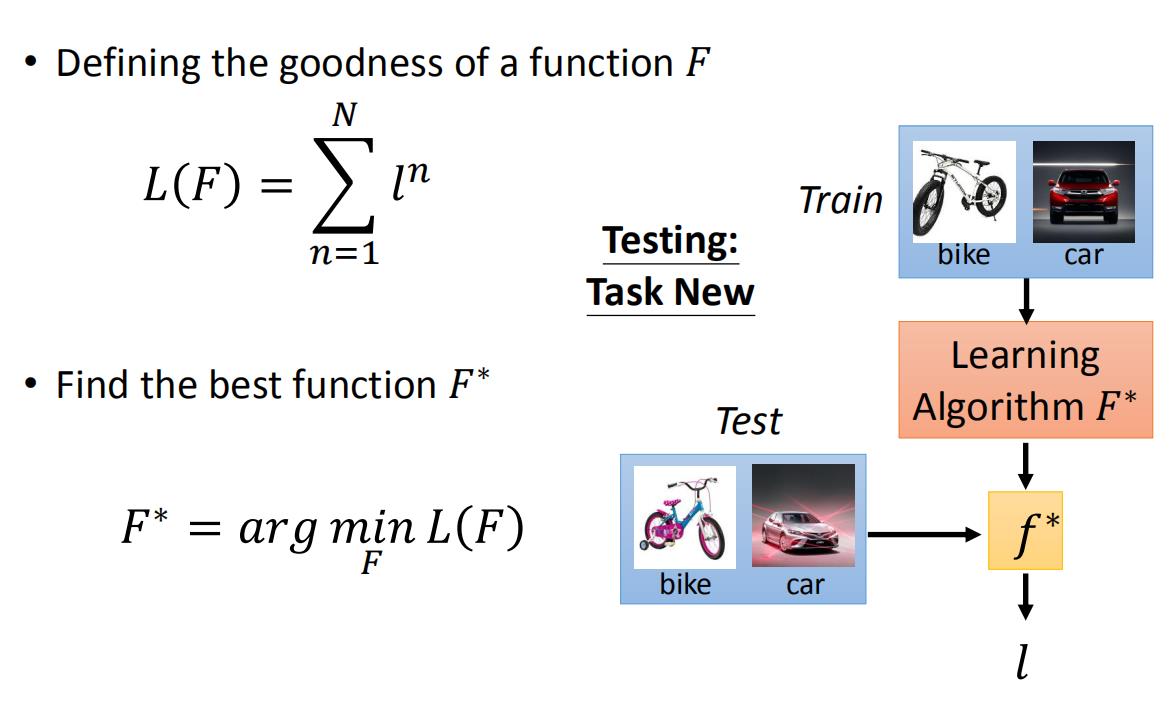
meta learning损失函数，就是$L（F）$，其实就是每一个训练子任务loss function总和。之后我们用梯度下降的方法不断的更新$F$的参数，得到一个最好的$F^{\ast }$，之后我们将训练好的$F^{\ast }$放入到测试任务集中进行测试，比如第一个测试任务是一个自行车汽车识别器，我们先将少量训练数据放入到$F^{\ast }$中，之后得到一个分类器$f^{\ast }$，之后我们将测试数据放入到$f^{\ast }$中，得到最终的loss，作为这次测试的结果。

4、元学习过程总结

设$\mathcal{X}$为输入的空间， 和$\mathcal{Y}$是一个离散的标签空间。设$\mathcal{D}$为$\mathcal{X}\times \mathcal{Y}$的分布。监督机器学习通常旨在通过对参数化模型和训练集应用学习算法捕获条件分布$p(y\mid x)$， $S_{\text{train}}=$ { ( x i , y i ) ∼ D } i = 1 N . \\left\\{\\left(x_{i}, y_{i}\\right) \\sim \\mathcal{D}\\right\\}_{i=1}^{N} . {(xi​,yi​)∼D}i=1N​.在推理时，模型在测试输入$x$上进行评估，以估计$p(y\mid x)$。推理和学习算法的组合可以写成函数$h$(一种分类算法)以训练集作为输入，测试输入$x$，并在标签上输出估计概率分布$\hat{\mathbf{p}}$:
$$\hat{\mathbf{p}}(x)=h\left(x,S_{\text{train }}\right)$$
在few-shot学习中，我们希望函数$h$即使在$S_{\text{train}}$很小的情况下也具有较高的分类精度。Meta learning是一个涵盖了许多最近提出的经验风险最小化方法的术语。具体来说，他们考虑了参数化分类算法$h(\cdot ，\cdot ;\mathbf{w})$，并尝试估计一个“好的”参数向量$\mathbf{w}$，即对应于一个可以很好地从小数据集学习的分类算法。因此，估计这个参数向量可以理解为元学习。

元学习算法有两个阶段。第一阶段是元训练，估计分类算法的参数向量$\mathrm{w}$。

• 在元训练过程中，元学习者可以访问一个大型标记数据集$S_{\text{meta}}$，该数据集通常包含大量类的数千张图像$C$ . 在元训练的每次迭代中，元学习者从 $S_{\text{meta}}$中抽取一个分类问题样本。也就是说，元学习者首先从$C$中抽取$m$类的子集，然后抽取小的"training" 集合 $S_{\text{train }}$ 和小的"test" 集合 $S_{\text{test }}.$
• 然后，它使用当前的权重向量$\mathbf{w}$来计算条件概率$h\left(x,S_{\text{train}};\mathbf{w}\right)$用于测试集 S test S_{\\text {test}}

  以上是关于8.7 Meta learning元学习全面理解MAMLReptile的主要内容，如果未能解决你的问题，请参考以下文章

  元学习Meta-learning与MAML

  8.15 SNAIL：神经注意力元学习

  Meta Learning(元学习)详解

  Meta Learning(元学习)详解

  Meta Learning(元学习)详解

  卡耐基梅隆大学（CMU）元学习和元强化学习课程 | Elements of Meta-Learning