8.13 Prototypical Networks 原型网络
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了8.13 Prototypical Networks 原型网络相关的知识,希望对你有一定的参考价值。
文章目录
8.7 Meta learning元学习全面理解、MAML、Reptile
prototypical networks (原型网络) 解决few-shot 分类问题 的元学习方法。
few-shot 分类就是test data 有很多新的类,每个新类的只有少量例子。
原型网络学习一个embedding空间,在这个空间中,分类可以通过计算每个类的原型表示的距离来执行。
1、前言
对于few-shot learning ,原型网络将输入经过非线性映射到embedding空间,对每一个类的support数据的embedding求均值,然后将这个均值作为该类的原型,对新样例进行预测的时候,观察新样例embedding和这些原型哪个最接近便分到该类别。
对于zero-shot learning ,不是给一个support集得到聚类点,而是给每个类一个meta-data向量 v k v_k vk。通常而言是某个训练好的网络给出的feature map,并且文中使用的是一个线性模型将该meta-data vector映射为c,且将其进行归一化(文中的解释是说因为meta-data vector和query set样例来自不同domain,因此对meta-data进行归一化会比较有效)
图
一
图一
图一
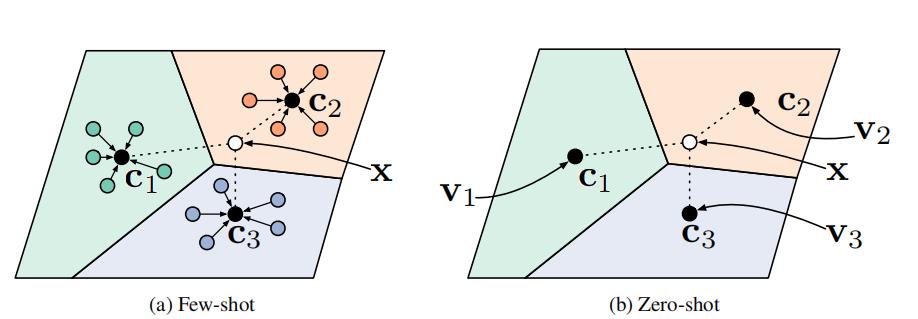
图一,左:Few-shot 原型 c k \\mathbf{c}_{k} ck被计算为每个类的support 数据embedding的平均值。右:Zero-shot 原型 c k \\mathbf{c}_{k} ck是通过embedding 类meta数据 v k . \\mathbf{v}_{k} . vk.产生的。在这两种情况下,新的点的嵌入通过一个到类原型的距离 ,加上softmax进行分类 p ϕ ( y = k ∣ x ) ∝ exp ( − d ( f ϕ ( x ) , c k ) ) p_{\\phi}(y=k \\mid \\mathbf{x}) \\propto \\exp \\left(-d\\left(f_{\\phi}(\\mathbf{x}), \\mathbf{c}_{k}\\right)\\right) pϕ(y=k∣x)∝exp(−d(fϕ(x),ck)).
2、Prototypical Networks
2.1、 符号
few-shot 分类数据有N类很少support set 示例: S = S= S= { ( x 1 , y 1 ) , … , ( x N , y N ) } \\left\\{\\left(\\mathbf{x}_{1}, y_{1}\\right), \\ldots,\\left(\\mathbf{x}_{N}, y_{N}\\right)\\right\\} {(x1,y1),…,(xN,yN)} , x i ∈ R D \\mathbf{x}_{i} \\in \\mathbb{R}^{D} xi∈RD是一个示例 D D D维特征向量。 y i ∈ { 1 , … , K } y_{i} \\in\\{1, \\ldots, K\\} yi∈{1,…,K}为标签, S k S_{k} Sk表示用类 k k k标记的一组示例。
2.2 模型
每个类通过嵌入函数
f
ϕ
:
R
D
→
R
M
f_{\\phi}: \\mathbb{R}^{D} \\rightarrow \\mathbb{R}^{M}
fϕ:RD→RM,参数
ϕ
.
\\phi .
ϕ. Prototypical networks 计算一个
M
M
M维表征
c
k
∈
R
M
\\mathbf{c}_{k} \\in \\mathbb{R}^{M}
ck∈RM 或原型,原型是 support 点平均embedding
c
k
=
1
∣
S
k
∣
∑
(
x
i
,
y
i
)
∈
S
k
f
ϕ
(
x
i
)
(1)
\\mathbf{c}_{k}=\\frac{1}{\\left|S_{k}\\right|} \\sum_{\\left(\\mathbf{x}_{i}, y_{i}\\right) \\in S_{k}} f_{\\phi}\\left(\\mathbf{x}_{i}\\right)\\tag{1}
ck=∣Sk∣1(xi,yi)∈Sk∑fϕ(xi)(1)
给定一个距离函数
d
:
R
M
×
R
M
→
[
0
,
+
∞
)
d: \\mathbb{R}^{M} \\times \\mathbb{R}^{M} \\rightarrow[0,+\\infty)
d:RM×RM→[0,+∞),使用softmax度量查询点
x
\\mathrm{x}
x在嵌入空间中到原型的距离的大小
p
ϕ
(
y
=
k
∣
x
)
=
exp
(
−
d
(
f
ϕ
(
x
)
,
c
k
)
)
∑
k
′
exp
(
−
d
(
f
ϕ
(
x
)
,
c
k
′
)
)
(2)
p_{\\phi}(y=k \\mid \\mathbf{x})=\\frac{\\exp \\left(-d\\left(f_{\\phi}(\\mathbf{x}), \\mathbf{c}_{k}\\right)\\right)}{\\sum_{k^{\\prime}} \\exp \\left(-d\\left(f_{\\phi}(\\mathbf{x}), \\mathbf{c}_{k^{\\prime}}\\right)\\right)}\\tag{2}
pϕ(y=k∣x)=∑k′exp(−d(fϕ(x),ck′))exp(−d(fϕ(x),ck))(2)
通过SGD最小化真正的类
k
k
k的负对数似然:
J
(
ϕ
)
=
−
log
p
ϕ
(
y
=
k
∣
x
)
(3)
J(\\phi)=-\\log p_{\\phi}(y=k \\mid \\mathbf{x})\\tag{3}
J(ϕ)=−logpϕ(y=k∣x)(3)
训练集是通过从训练集中随机选取类的一个子集,然后在每个类中选取样本的一个子集作为support 集,其余样本的一个子集作为query 点来形成的。在算法1中提供了计算一个训练集损失
J
(
ϕ
)
J(\\phi)
J(ϕ)的伪代码。
算法1 :原型网络的训练集损失计算。 N N N为训练集中的样本数, K K K为训练集中的类数, N C ≤ K N_{C} \\leq K NC≤K为每段的类数, N S N_{S} NS为每类的support 样本数, N Q N_{Q} NQ为每类的query 样本数。RANDOMSAMPLE ( S , N ) (S, N) (S,N)表示从集合 S S S中均匀随机选择的一组 N N N元素,不进行替换。
Input: 训练集 D = { ( x 1 , y 1 ) ,
以上是关于8.13 Prototypical Networks 原型网络的主要内容,如果未能解决你的问题,请参考以下文章