动态规划经典题之编辑距离

Posted 2021-06-29 快乐江湖

文章目录

• 题目
• 解题思路
• • （1）基本过程
  • （2）动态规划-递归
  • （3）动态规划-dp table
• 代码

题目

leetCode72:编辑距离

编辑距离算法是一个非常实用的算法，它的作用是求出把一个字符串s1变为另一个字符串s2所需要的最少的操作数。
此过程中，只能对字符串进行插入、删除或替换（其实还有一种隐形操作，就是略过）

比如把rad变为apple，就需要经过5步

解题思路

（1）基本过程

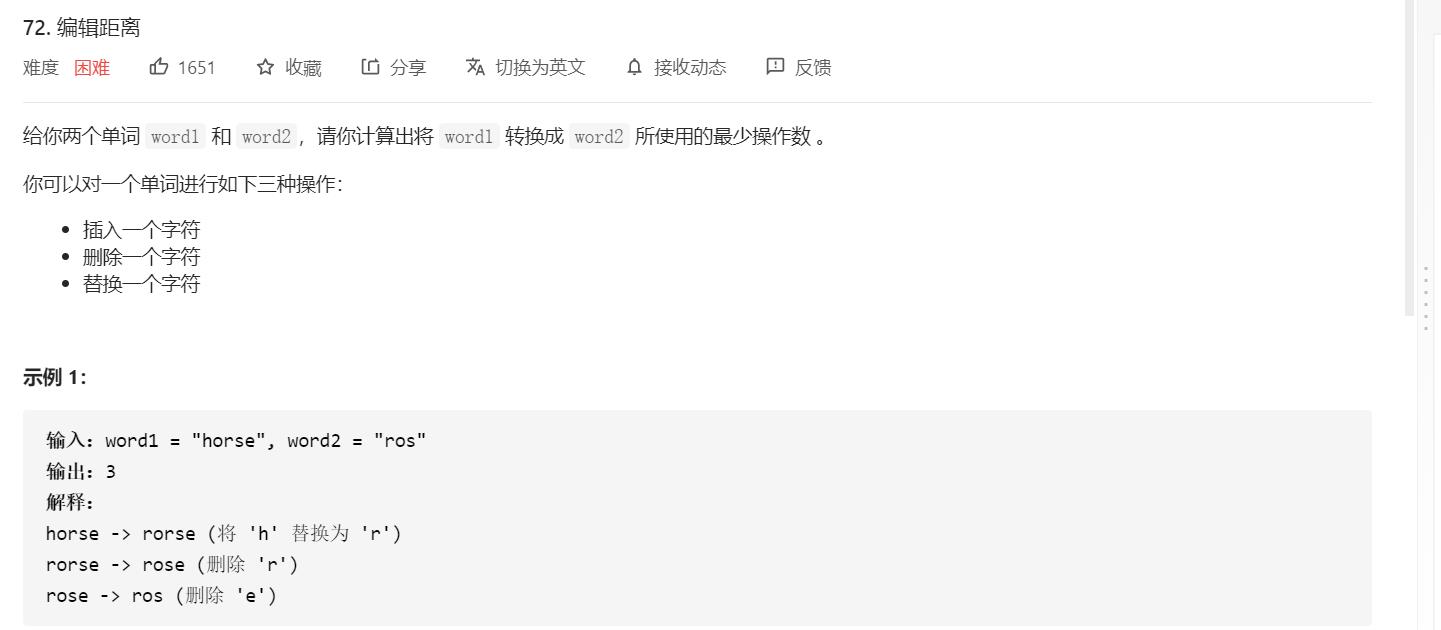
对于字符串类的题目，一般都会使用到两个指针，这里面也不例外。上面的动图中，展现的正是两个指针i和j分别从后向前扫描两个字符串。
在这个过程中如果j走完了，i还没有走完的话，那么就需要把s1删除，缩短为s2单

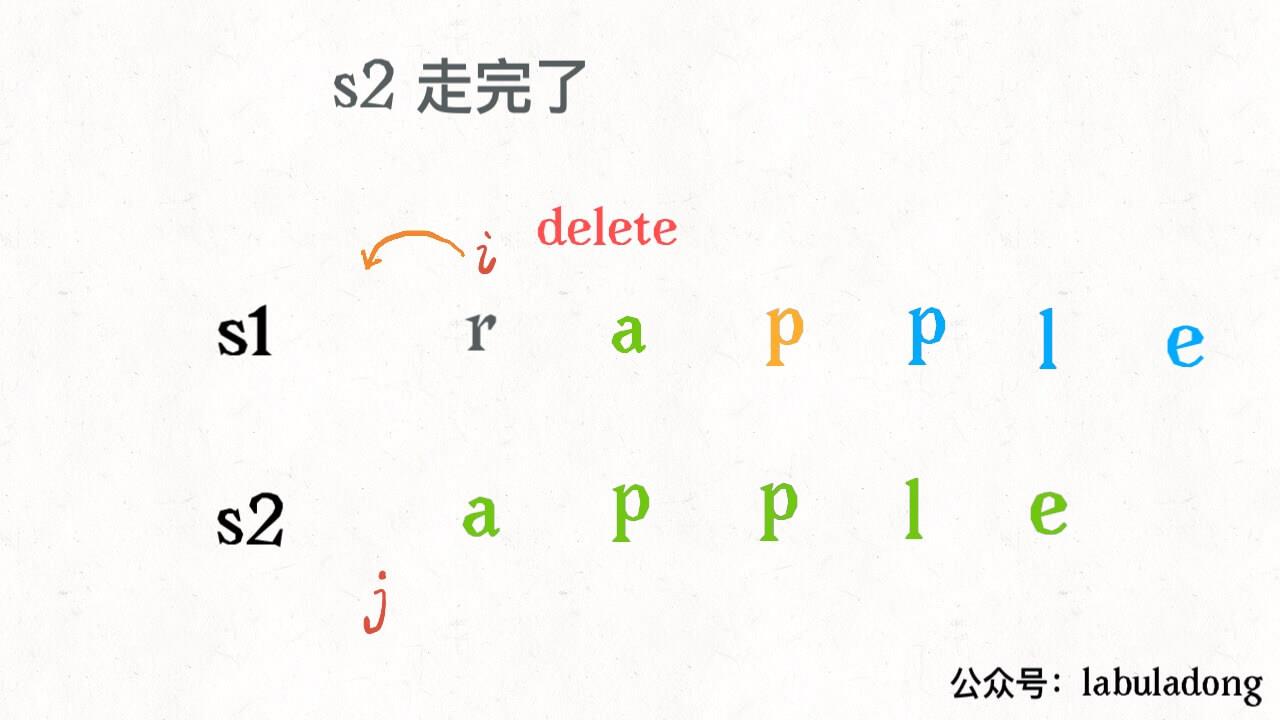
如果i走完了，但j没有走完，那么就想要把s2中的插入到s1中

（2）动态规划-递归

使用动态规划解题，一定要考虑题目的状态和选择是什么？

• 状态：这里显然是i和j指针的位置
• 选择：所选的操作，加上跳过，共有四种操作（skip，insert，delete，replace）

if s1[i]==s2[j]
	skip;
else
	insert or delete or relace;

还有“base case”，也就是最简单的情况是什么呢？这里其实就是上面所叙述的那两种情况

首先采用递归解法说明。定义一个dp递归函数，函数形参分别就是i和j，该函数的返回值就是s1[0....i]和s2[0...j]的最小编辑距离，最终一步一步递归，可以得到问题的最终答案。

现在看该函数的base case，也就是如果j走完了，就把i删除了；如果i走完了，就把j剩下的全部插入

int dp(i,j)
{
	if i==-1
		return j+1;
	if j==-1
		return i+1;
}

如果遇到的字符相等，那么就什么也不做，直接跳过。也即是说s1[0....i]和s2[0....j]的最小编辑距离实际就是s1[0...i-1]和s2[0....j-1]的最小编辑距离。

int dp(i,j)
{
	if i==-1
		return j+1;
	if j==-1
		return i+1;
	if(s1[i]==s[j])
		return dp[i-1][j-1];
	else
	
}

如果遇到的字符不相等，那么我们就需要进行选择三种操作了。需要注意的是三种操作是肯定存在重叠问题，这也是递归不可避免的问题，因为一个字符变成另一个字符除了可以替换外，我也可以直接插入一个。

• 第一种操作：插入；递归函数为dp(i,j-1)+1。如果选择了这种操作，那么就会直接在s1[i]中插入一个和s2[j]一样的字符，此时s2[j]会被匹配到。注意操作数+1
  

• 第二种操作：删除；递归函数为dp(i-1,j)+1。如果选择了这种操作，那么就会直接把s[i]这个字符删除掉。
  

• 第三种操作：替换；递归函数为dp(i-1,j-1)+1。如果选择了这种操作就会直接把s1[i]替换为s2[j]。

于是伪代码如下

int dp(i,j)
{
	if i==-1
		return j+1;
	if j==-1
		return i+1;
	if(s1[i]==s[j])
		return dp[i-1][j-1];
	else
		return min(
		dp(i,j-1)+1;//插入
		dp(i-1,j)+1;//删除
		dp(i-1,j-1)+1;//替换
	)
}

还是那句话，这种解法一定存在大量重叠子问题。比如能过替换得到的结果也可以通过删除后插入完成，这就是一条重复路径，如果发现了一定重复问题，那么一定会有千千万万个重复问题，就像斐波那契数列一样。而重叠子问题是可以通过备忘录解决的

memo=dict();
int dp(i,j)
{
	if((i,j) in memo)
		return memo[(i,j)];
	if i==-1
		return j+1;
	if j==-1
		return i+1;
	if(s1[i]==s[j])
		return dp[i-1][j-1];
	else
		return min(
		dp(i,j-1)+1;//插入
		dp(i-1,j)+1;//删除
		dp(i-1,j-1)+1;//替换
	)
}

（3）动态规划-dp table

递归便于说明问题的解决思路，实际写代码时我们一般采用的还是自底向上的解法，也就是动态规划数组。有了上面的基础，我们很容易能够理解，和公共子串，子序列那些题一样**，这道题的数组也一定是一个二维数组**

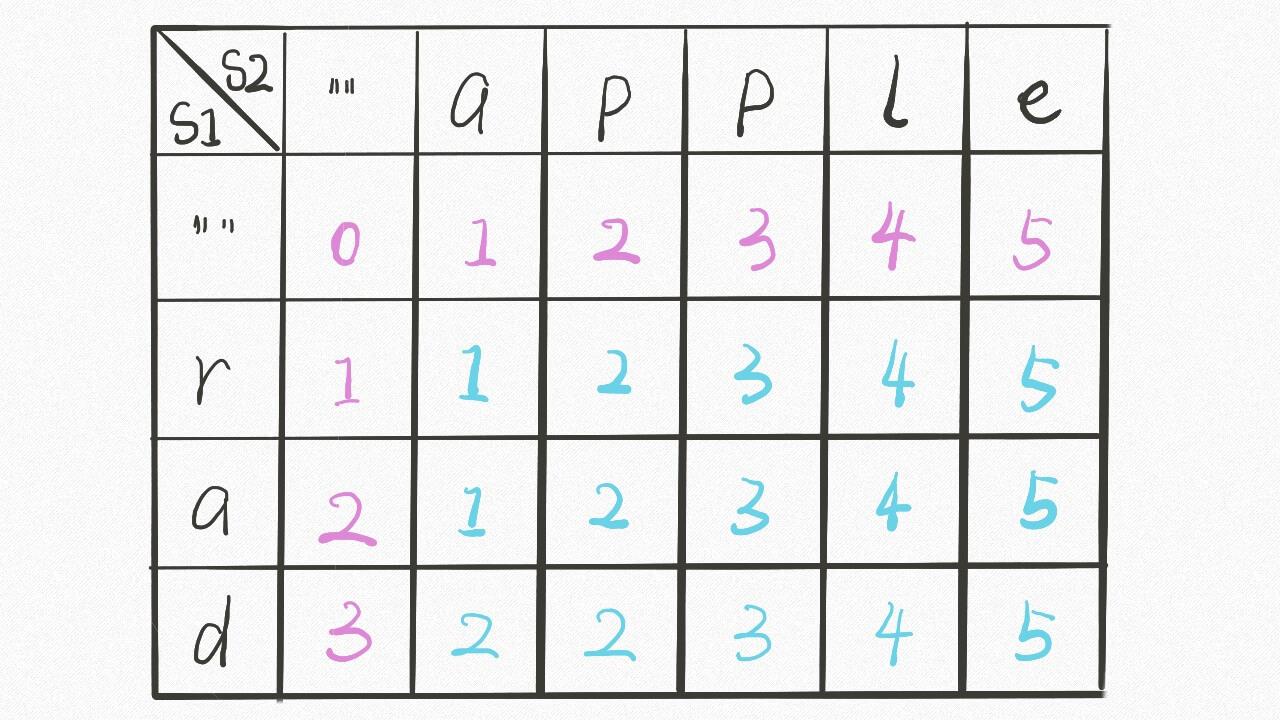
其中dp[…][0]和dp[0][…]对应的就是base case（也即是把rad变成空串，那么需要3步），dp[i][j]存储的是s1[0…i-1]和s2[0…j-1]的最小编辑距离。（dp函数的base case是i和j为-1，但是数组索引至少为0，所以要偏移1位）

代码

class Solution {
public:
    
    int minDistance(string word1, string word2) 
    {
        int len1=word1.size();
        int len2=word2.size();
        
        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));//dp数组
        for(int i=1;i<=len1;i++)//base case
            dp[i][0]=i;
        for(int j=1;j<=len2;j++)
            dp[0][j]=j;
        
        for(int i=1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(word1[i-1]==word2[j-1])
                    dp[i][j]=dp[i-1][j-1];
                else
                    dp[i][j]=min//min函数只有两个形参，所以这样写
                (
                    dp[i-1][j]+1,//插入
                    min(dp[i][j-1]+1,//删除
                    dp[i-1][j-1]+1)//替换
                );
                    
            }
        }
        return dp[len1][len2];
    }
};