17、频率模型-泊松分布
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了17、频率模型-泊松分布相关的知识,希望对你有一定的参考价值。
参考技术A 17、频率模型-泊松分布from functools import partial
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import mean_tweedie_deviance
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder
from sklearn.preprocessing import StandardScaler, KBinsDiscretizer
from sklearn.metrics import mean_absolute_error, mean_squared_error
def load_mtpl2(n_samples=100000):
# freMTPL2freq dataset from https://www.openml.org/d/41214
df_freq = fetch_openml(data_id=41214, as_frame=True)['data']
df_freq['IDpol'] = df_freq['IDpol'].astype(np.int)
df_freq.set_index('IDpol', inplace=True)
# freMTPL2sev dataset from https://www.openml.org/d/41215
df_sev = fetch_openml(data_id=41215, as_frame=True)['data']
# sum ClaimAmount over identical IDs
df_sev = df_sev.groupby('IDpol').sum()
df = df_freq.join(df_sev, how="left")
df["ClaimAmount"].fillna(0, inplace=True)
# unquote string fields
for column_name in df.columns[df.dtypes.values == np.object]:
df[column_name] = df[column_name].str.strip("'")
return df.iloc[:n_samples]
def plot_obs_pred(df, feature, weight, observed, predicted, y_label=None,
title=None, ax=None, fill_legend=False):
# aggregate observed and predicted variables by feature level
df_ = df.loc[:, [feature, weight]].copy()
df_["observed"] = df[observed] * df[weight]
df_["predicted"] = predicted * df[weight]
df_ = (
df_.groupby([feature])[[weight, "observed", "predicted"]]
.sum()
.assign(observed=lambda x: x["observed"] / x[weight])
.assign(predicted=lambda x: x["predicted"] / x[weight])
)
ax = df_.loc[:, ["observed", "predicted"]].plot(style=".", ax=ax)
y_max = df_.loc[:, ["observed", "predicted"]].values.max() * 0.8
p2 = ax.fill_between(
df_.index,
0,
y_max * df_[weight] / df_[weight].values.max(),
color="g",
alpha=0.1,
)
if fill_legend:
ax.legend([p2], [" distribution".format(feature)])
ax.set(
ylabel=y_label if y_label is not None else None,
title=title if title is not None else "Train: Observed vs Predicted",
)
def score_estimator(
estimator, X_train, X_test, df_train, df_test, target, weights,
tweedie_powers=None,
):
"""Evaluate an estimator on train and test sets with different metrics"""
metrics = [
("D² explained", None), # Use default scorer if it exists
("mean abs. error", mean_absolute_error),
("mean squared error", mean_squared_error),
]
if tweedie_powers:
metrics += [(
"mean Tweedie dev p=:.4f".format(power),
partial(mean_tweedie_deviance, power=power)
) for power in tweedie_powers]
res = []
for subset_label, X, df in [
("train", X_train, df_train),
("test", X_test, df_test),
]:
y, _weights = df[target], df[weights]
for score_label, metric in metrics:
if isinstance(estimator, tuple) and len(estimator) == 2:
# Score the model consisting of the product of frequency and
# severity models.
est_freq, est_sev = estimator
y_pred = est_freq.predict(X) * est_sev.predict(X)
else:
y_pred = estimator.predict(X)
if metric is None:
if not hasattr(estimator, "score"):
continue
score = estimator.score(X, y, sample_weight=_weights)
else:
score = metric(y, y_pred, sample_weight=_weights)
res.append(
"subset": subset_label, "metric": score_label, "score": score
)
res = (
pd.DataFrame(res)
.set_index(["metric", "subset"])
.score.unstack(-1)
.round(4)
.loc[:, ['train', 'test']]
)
return res
df = load_mtpl2(n_samples=60000)
# Note: filter out claims with zero amount, as the severity model
# requires strictly positive target values.
df.loc[(df["ClaimAmount"] == 0) & (df["ClaimNb"] >= 1), "ClaimNb"] = 0
# Correct for unreasonable observations (that might be data error)
# and a few exceptionally large claim amounts
df["ClaimNb"] = df["ClaimNb"].clip(upper=4)
df["Exposure"] = df["Exposure"].clip(upper=1)
df["ClaimAmount"] = df["ClaimAmount"].clip(upper=200000)
log_scale_transformer = make_pipeline(
FunctionTransformer(func=np.log),
StandardScaler()
)
column_trans = ColumnTransformer(
[
("binned_numeric", KBinsDiscretizer(n_bins=10),
["VehAge", "DrivAge"]),
("onehot_categorical", OneHotEncoder(),
["VehBrand", "VehPower", "VehGas", "Region", "Area"]),
("passthrough_numeric", "passthrough",
["BonusMalus"]),
("log_scaled_numeric", log_scale_transformer,
["Density"]),
],
remainder="drop",
)
X = column_trans.fit_transform(df)
# Insurances companies are interested in modeling the Pure Premium, that is
# the expected total claim amount per unit of exposure for each policyholder
# in their portfolio:
df["PurePremium"] = df["ClaimAmount"] / df["Exposure"]
# This can be indirectly approximated by a 2-step modeling: the product of the
# Frequency times the average claim amount per claim:
df["Frequency"] = df["ClaimNb"] / df["Exposure"]
df["AvgClaimAmount"] = df["ClaimAmount"] / np.fmax(df["ClaimNb"], 1)
with pd.option_context("display.max_columns", 15):
print(df[df.ClaimAmount > 0].head())
df_train, df_test, X_train, X_test = train_test_split(df, X, random_state=0)
# The parameters of the model are estimated by minimizing the Poisson deviance
# on the training set via a quasi-Newton solver: l-BFGS. Some of the features
# are collinear, we use a weak penalization to avoid numerical issues.
glm_freq = PoissonRegressor(alpha=1e-3, max_iter=400)
glm_freq.fit(X_train, df_train["Frequency"],
sample_weight=df_train["Exposure"])
scores = score_estimator(
glm_freq,
X_train,
X_test,
df_train,
df_test,
target="Frequency",
weights="Exposure",
)
print("Evaluation of PoissonRegressor on target Frequency")
print(scores)
fig, ax = plt.subplots(ncols=2, nrows=2, figsize=(16, 8))
fig.subplots_adjust(hspace=0.3, wspace=0.2)
plot_obs_pred(
df=df_train,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_train),
y_label="Claim Frequency",
title="train data",
ax=ax[0, 0],
)
plot_obs_pred(
df=df_test,
feature="DrivAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[0, 1],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="VehAge",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 0],
fill_legend=True
)
plot_obs_pred(
df=df_test,
feature="BonusMalus",
weight="Exposure",
observed="Frequency",
predicted=glm_freq.predict(X_test),
y_label="Claim Frequency",
title="test data",
ax=ax[1, 1],
fill_legend=True
)
泊松分布
泊松分布泊松分布适用于在随机时间和空间上发生事件的情况,其中,我们只关注事件发生的次数。
当以下假设有效时,则称为泊松分布:
* 任何一个成功的事件都不应该影响另一个成功的事件。
* 在短时间内成功的概率必须等于在更长的时间内成功的概率。
* 时间间隔很小时,成功的概率趋近于零。
??是事件发生的频率,也就是单位时间(或单位面积内随机事件的平均发生率),t是时间间隔,X是该时间间隔内的事件数。X称为泊松随机变量,X的概率分布称为泊松分布。??表示长度为t的时间间隔中的平均事件数,那么??=??*t。
通俗定义:假定一个事件在一段时间内随机发生,且符合以下条件:
* 将该时间段无限分隔成若干个小的时间段,在这个接近于零的小时间段内,该事件发生一次的概率与这个极小时间段的长度成正比。
* 在每一个极小时间段内,该事件发生两次及两次以上的概率恒等于零。
* 该事件在不同的小时间段内,发生与否相互独立。
公式:
$$fleft( x|lambda
ight) =dfrac {lambda ^{x}e^{-lambda }}{x!}$$
泊松分布相关代码
#导入库 import numpy as np import scipy.stats as stats import matplotlib.pyplot as plt from collections import Counter
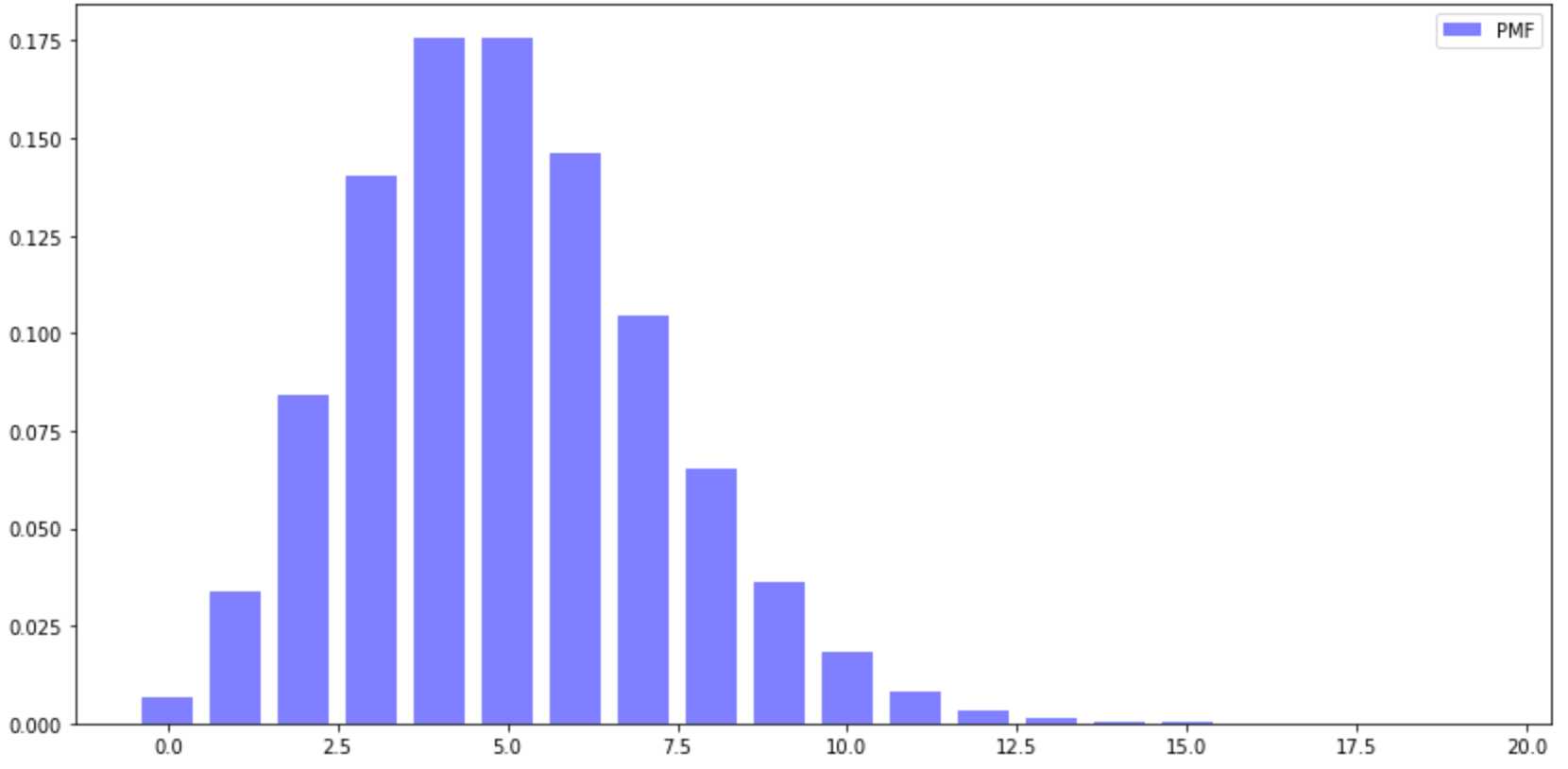
PMF
#PMF plt.figure(figsize=(14,7)) x=np.arange(20) y=stats.poisson.pmf(x,mu=5) plt.figure(figsize=(14,7)) plt.bar(x, y, width=0.75, alpha=0.5, color=‘b‘, label=‘PMF‘, ) plt.legend() plt.show()
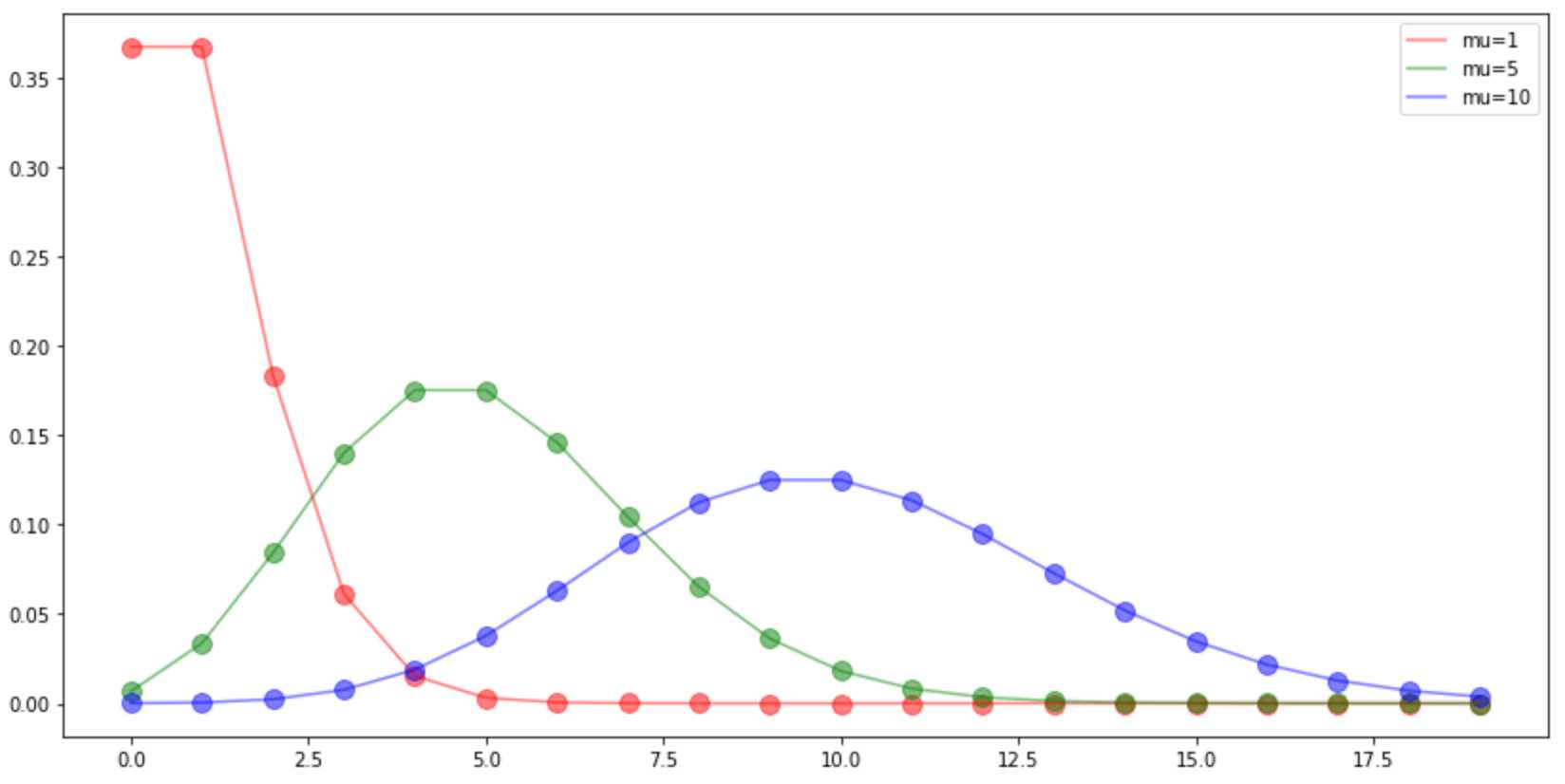
??值的影响
#??值不同 plt.figure(figsize=(14,7)) x=np.arange(20) y1=stats.poisson.pmf(x,mu=1) y2=stats.poisson.pmf(x,mu=5) y3=stats.poisson.pmf(x,mu=10) plt.scatter(x, y1, alpha=0.5, color=‘r‘, s=100, ) plt.plot(x, y1, alpha=0.5, color=‘r‘, label=‘mu=1‘, ) plt.scatter(x, y2, alpha=0.5, color=‘g‘, s=100, ) plt.plot(x, y2, alpha=0.5, color=‘g‘, label=‘mu=5‘, ) plt.scatter(x, y3, alpha=0.5, color=‘b‘, s=100, ) plt.plot(x, y3, alpha=0.5, color=‘b‘, label=‘mu=10‘, ) plt.legend() plt.show()
随机样本
#随机样本 np.random.seed(0) print(stats.poisson.rvs(mu=10),end=‘ ‘) print(stats.poisson.rvs(mu=10,size=10),end=‘ ‘)
![]()
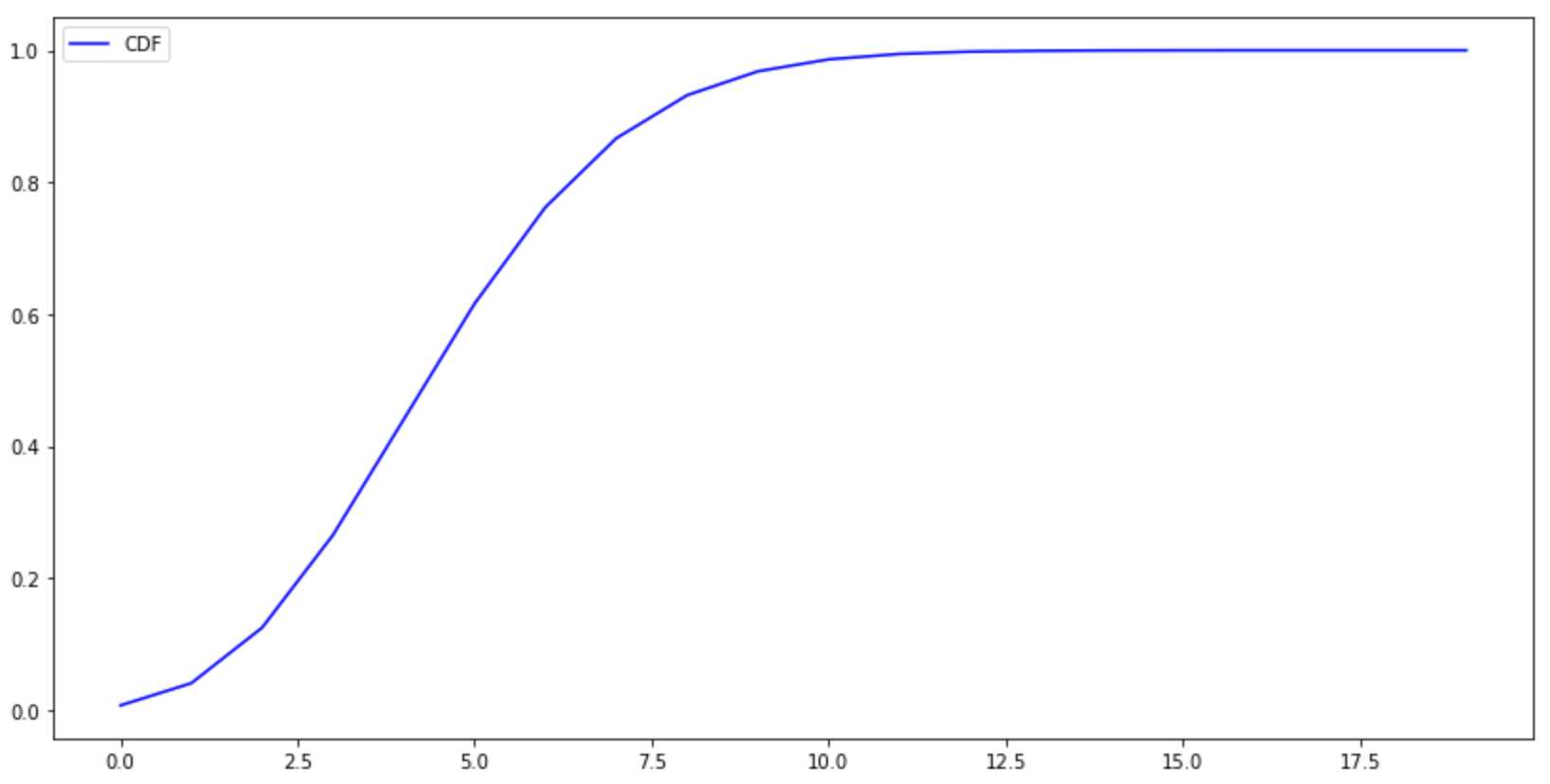
CDF
#CDF x=np.arange(20) y=stats.poisson.cdf(x,mu=5) plt.figure(figsize=(14,7)) plt.plot(x, y, color=‘b‘, label=‘CDF‘ ) plt.legend() plt.show()
区间概率
print(‘P(X<3)={}‘.format(stats.poisson.cdf(k=3,mu=5))) print(‘P(2<X<=8)={}‘.format(stats.poisson.cdf(k=8,mu=5)-stats.poisson.cdf(k=2,mu=5)))
![]()
以上是关于17、频率模型-泊松分布的主要内容,如果未能解决你的问题,请参考以下文章