红黑树插入与删除

Posted 2021-07-02 bbhzs

1. 红黑树的定义

（1）红黑树要解决的主要问题：防止二叉树退化为链表，导致查询性能降为O(n)。

（2）红黑树是一棵二叉查找树。

（3）红黑树的插入、删除、查询时间复杂度为O(log n)。

---

2.  红黑树的性质

（1）性质1：树中的每个节点都是红节点或者黑节点。

（2）性质2：根节点是黑节点。

（3）性质3：叶子节点（nil节点）为黑节点。

（4）性质4：红节点的孩子必须是黑节点。

（5）性质5：从任意一个节点出发，到达叶子节点的路径，所含有的黑节点数目相等。

---

3.  红黑树的插入

注意：插入的节点必须为红节点。

情况1(特殊情况)：插入节点为根节点、插入节点的父节点为黑节点。

情况2：插入节点的父节点为红节点，并且叔叔节点为黑节点。（4种小情况）

情况3：插入节点的父节点为红节点，并且叔叔节点为红节点。（4种小情况）

情况1处理：将新插入节点颜色变为黑色。

情况2处理：可以拆分为4中小情况，从上到下，第一个红节点为父节点，第二个节点为新插入红节点。

情况3处理：x为新插入节点，y为父节点，u为叔叔点，z为祖父节点；将有、u变为黑色、z变为红色；把z看成新插入节点，递归操作。

---

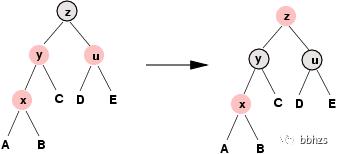
4. 红黑树的删除

三种大情况：

大情况1：删除节点没有孩子节点。

大情况2：删除节点只有一个孩子节点。

大情况3：删除节点有两个孩子节点。通过查找前驱节点或者后继节点转化为大情况1或者大情况2。

双黑节点：对于大情况1，直接把删除节点看作双黑节点；对于大情况2，先删除节点，之后使用孩子节点取代删除节点的位置，包括颜色和数值，并且把代替节点看作双黑节点；大情况3转化后，对应大情况1或者大情况2。

引入双黑节点后，删除算法可以划分为以下4种情况：

小情况1：双黑节点是红色或者根节点；把双黑节点变黑，之后根据大情况1或者大情况2进行相关操作。

注意：情况1之后，下面各种情况，都说明双黑节点是黑节点，并且不是根节点。其实，也只有大情况1会出现下面各种情况。

小情况2：双黑节点的兄弟节点是红节点；把父节点y左旋；将双黑节点的父节点y变为红色，双黑节点兄弟节点z变为红色；之后转化为情况3或者情况4处理。并且，双黑节点仍然不变，只是父子关系发生变化而已。

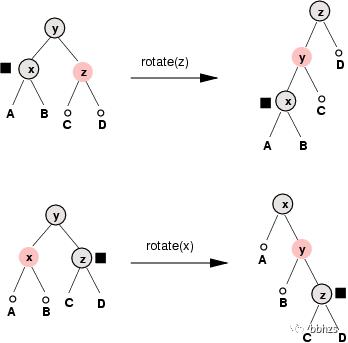
小情况3：双黑节点的兄弟是黑节点，并且他的两个孩子也是黑节点（都是空姐点）；将双黑节点的兄弟变红；把双黑节点的父节点看成双黑节点，进行递归操作。

小情况4：双黑色结点有一个黑色兄弟结点，并且黑色兄弟节点至少有一个红孩子。对双黑节点的兄弟节点进行左旋或者右旋操作，使得孩子节点在上方；把双黑兄弟节点的颜色变红，其孩子节点的颜色变黑；把双黑节点兄弟节点颜色和父节点颜色互换；再次对父节点进行左旋或者右旋。

---

5. JDK1.8 TreeMap分析环节

（1）把P节点作为顶层节点左旋

/** From CLR */ private void rotateLeft(Entry<K,V> p) { if (p != null) { Entry<K,V> r = p.right; p.right = r.left; if (r.left != null) r.left.parent = p; r.parent = p.parent; if (p.parent == null) root = r; else if (p.parent.left == p) p.parent.left = r; else p.parent.right = r; r.left = p; p.parent = r; } }

（2）把P节点作为顶层节点右旋

 /** From CLR */ private void rotateRight(Entry<K,V> p) { if (p != null) { Entry<K,V> l = p.left; p.left = l.right; if (l.right != null) l.right.parent = p; l.parent = p.parent; if (p.parent == null) root = l; else if (p.parent.right == p) p.parent.right = l; else p.parent.left = l; l.right = p; p.parent = l; } }

（3）获取后继节点

/** * Returns the successor of the specified Entry, or null if no such. */ static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) { if (t == null) return null; else if (t.right != null) { Entry<K,V> p = t.right; while (p.left != null) p = p.left; return p; } else { Entry<K,V> p = t.parent; Entry<K,V> ch = t; while (p != null && ch == p.right) { ch = p; p = p.parent; } return p; } }

（4）获取前驱节点

/** * Returns the predecessor of the specified Entry, or null if no such. */ static <K,V> Entry<K,V> predecessor(Entry<K,V> t) { if (t == null) return null; else if (t.left != null) { Entry<K,V> p = t.left; while (p.right != null) p = p.right; return p; } else { Entry<K,V> p = t.parent; Entry<K,V> ch = t; while (p != null && ch == p.left) { ch = p; p = p.parent; } return p; } }

（5）插入节点算法流程

public V put(K key, V value) {// 类似二叉查找树插入操作 Entry<K,V> t = root;        if (t == null) { //特殊情况，插入根节点            compare(key, key); // type (and possibly null) check root = new Entry<>(key, value, null); size = 1; modCount++; return null; } int cmp; Entry<K,V> parent; // split comparator and comparable paths Comparator<? super K> cpr = comparator; if (cpr != null) { do { parent = t; cmp = cpr.compare(key, t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } else { if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } Entry<K,V> e = new Entry<>(key, value, parent); if (cmp < 0) parent.left = e; else parent.right = e;        fixAfterInsertion(e); // 插入之后进行修复 size++; modCount++; return null; }

（6）插入节点后fix流程

/** From CLR */ private void fixAfterInsertion(Entry<K,V> x) {        x.color = RED; while (x != null && x != root && x.parent.color == RED) { if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { Entry<K,V> y = rightOf(parentOf(parentOf(x)));                if (colorOf(y) == RED) { // 父节点为红节点、叔叔节点为红节点 setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED);                    x = parentOf(parentOf(x)); // 之后把父节点当初新插入节点递归                } else { // 父红、叔叔黑                    if (x == rightOf(parentOf(x))) { // LR x = parentOf(x); rotateLeft(x); // 对父节点左旋 } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x))); }            } else { // 对称性操作 Entry<K,V> y = leftOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { if (x == leftOf(parentOf(x))) { x = parentOf(x); rotateRight(x); } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); } } } root.color = BLACK; }

（7）删除节点流程

/** * Delete node p, and then rebalance the tree. */private void deleteEntry(Entry<K,V> p) { modCount++; size--;
 // If strictly internal, copy successor's element to p and then make p // point to successor.        if (p.left != null && p.right != null) { // 大情况3            Entry<K,V> s = successor(p); // 转化为大情况1 或者 大情况2 p.key = s.key; p.value = s.value;            p = s; // 把后继节点看成双黑节点 } // p has 2 children
 // Start fixup at replacement node, if it exists. Entry<K,V> replacement = (p.left != null ? p.left : p.right);              if (replacement != null) { // 大情况2 // Link replacement to parent replacement.parent = p.parent; if (p.parent == null) root = replacement; else if (p == p.parent.left) p.parent.left = replacement; else p.parent.right = replacement;
 // Null out links so they are OK to use by fixAfterDeletion. p.left = p.right = p.parent = null;
            // Fix replacement replacement为双黑节点 if (p.color == BLACK) fixAfterDeletion(replacement); } else if (p.parent == null) { // return if we are the only node. root = null; } else { // No children. Use self as phantom replacement and unlink.           // 大情况1            if (p.color == BLACK) // p节点为双黑节点 fixAfterDeletion(p);
            if (p.parent != null) { // 删除节点，也可以放在前面进行操作 if (p == p.parent.left) p.parent.left = null; else if (p == p.parent.right) p.parent.right = null; p.parent = null; } }}

（8）删除节点fix过程

/** From CLR */private void fixAfterDeletion(Entry<K,V> x) {        while (x != root && colorOf(x) == BLACK) { // x为双黑节点 if (x == leftOf(parentOf(x))) { Entry<K,V> sib = rightOf(parentOf(x));
            if (colorOf(sib) == RED) { // 小情况2 setColor(sib, BLACK); setColor(parentOf(x), RED); rotateLeft(parentOf(x));                sib = rightOf(parentOf(x)); // 转化为小情况3或者小情况4 }
 if (colorOf(leftOf(sib)) == BLACK &&              colorOf(rightOf(sib)) == BLACK) { // 小情况 3 setColor(sib, RED);              x = parentOf(x); // 递归操作 } else {              if (colorOf(rightOf(sib)) == BLACK) { // 小情况 4 setColor(leftOf(sib), BLACK); setColor(sib, RED); rotateRight(sib); sib = rightOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(rightOf(sib), BLACK); rotateLeft(parentOf(x)); x = root; } } else { // symmetric 对称性操作 Entry<K,V> sib = leftOf(parentOf(x));
 if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateRight(parentOf(x)); sib = leftOf(parentOf(x)); }
 if (colorOf(rightOf(sib)) == BLACK && colorOf(leftOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); } else { if (colorOf(leftOf(sib)) == BLACK) { setColor(rightOf(sib), BLACK); setColor(sib, RED); rotateLeft(sib); sib = leftOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(leftOf(sib), BLACK); rotateRight(parentOf(x)); x = root; } }        } setColor(x, BLACK);}

---

参考文献

http://files.cppblog.com/xingkongyun/rbavl.pdf