信号与系统教学设计样例说明-2021春季学期

Posted 2021-06-28 卓晴

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了信号与系统教学设计样例说明-2021春季学期相关的知识，希望对你有一定的参考价值。

简介：本文通过一次课程录像对于当时的这次课程设计进行了反思与记录。主要是为了应付课程申请的内容进行整理的。这次课程的实践对于今后的工作还是具有一定的启发意义。

关键词： 信号与系统，课程设计，课后分析

§01 教学设计说明

1、备课与课程设计

本文是申请2021年 一流本科课程建设 申请报告中必须提交报告的一部分。是对于在2021年春季学期清华大学 网络标杆课程 线上观摩活动课后的反思记录。

教学设计整体设计依赖于课程教学大纲教学环节构建，教学局部设计（备课环节）则由自行设计的 教学软件TEASOFT 进行承载，和本文所呈现的文字与图片不同。TEASOFT教学软件可以将备课中所涉及到教学环节、资源（内容呈现、批注引导、网络资源展示、课堂互动等）以更加灵活的方式记录，便于任课教师对课堂的统御。

2、课程背景

“信号与系统分析”是大学工科专业重要的专业基础课程，它的内容涵盖了对于确定性信号与线性时不变系统分析与综合的基本原理、方法，从连续时间信号到离散时间信号，从时域分析到变换域分析。其中傅里叶变换是课程内容的重要组成部分。本文所涉及到的课程设计是信号与系统课程进行到第十次课程，在由傅里叶级数分解引出傅里叶变换定义，并对典型信号的频谱特性介绍完之后，开始讲解傅里叶变换的性质。

傅里叶变换的性质教学既是课程的重点，又是课程的难点。这些变换数学性质具有非常丰富的物理内涵，集中反映了信号在时域中的各种运算操作在变换域内的表现形式，是联系傅里叶频谱分析原来与工程应用的桥梁。但性质众多又是教学的难点，所以在教学上，除了深入挖掘傅里叶变换性质自身内涵、关联之外，一个重要的因素就是在讲解这些性质之前能够引起学生们的足够兴趣。

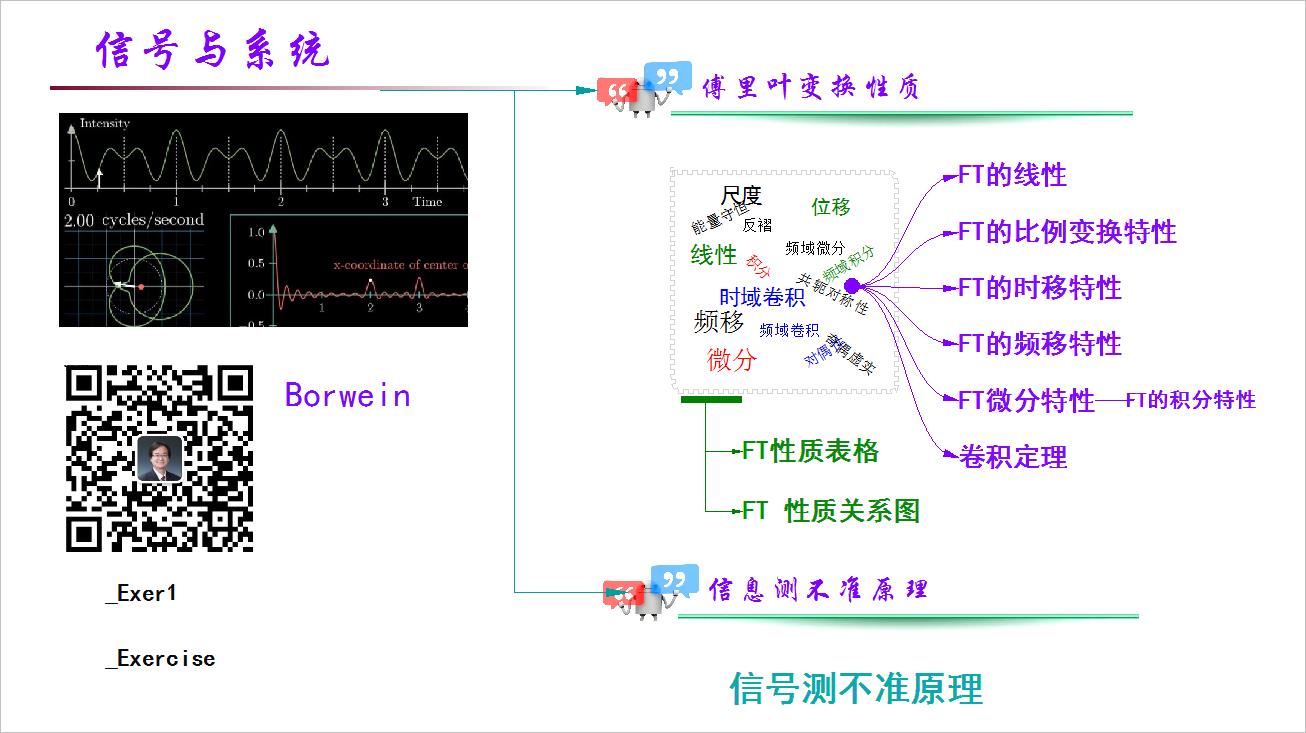
▲ 图1.1 第十次课程课件主要内容

^{▲ 图1.1 第十次课程课件主要内容}

这学期信号与系统课程面向两个班级，一个是以自动化系为主的大班（180人），一个是面向CDIE学生的小班（10人）。在教学环节与内容展示方面需要根据他们的特点略有不同。下面的教学设计主要是针对CDIE小班课程而制定的。CDIE小班学生专业背景与自动化系学生有一定差异，处在大三年级。前期电子类课程相对较弱，增加有美术、机械工程等跨学科内容。学生思辨能力强，专业兴趣广泛。

3、课堂交互软件

除了教学内容、课程参与主体（学生与教师）之外，教学环境与工具平台是教学设计另外一个重要因素。本次课程设计是基于小板课堂下，利用TEASOFT教学软件完成课堂教学形式设计。TEASOFT除了具有丰富的内容呈现、引导批注功能之外，与微信公众号（ TSINGHUAZHUOQING ）直接相连是支撑它进行教学互动的基础。本节课程设计中课程内容呈现与课堂讨论互动正式基于TEASOFT软件，它将参与课程学习同学们对问题的初步思考进行总结和呈现，触发参与思考，激励批判思维。

§02 课前教学设计

本次课程教学设计的背景前面已经介绍。下面给出课程准备器件对教学主要目标与教学环节设计。

1、课堂教学目标

讲解作业练习，复习信号卷积计算；
通过“数学虚幻模式”引入傅里叶变换性质学习；
了解傅里叶变换性质与信号运算之间的关系；
讲解傅里叶变换性质（前五个特性）：线性特性、尺度特性、时移与频移、微分与积分特性。

2、课程内容分解

基于前面教学目标，下面分别给出教学过程环节内容规划。

（1）讲解作业内容，复习信号卷积

通过之前作业中的问题课堂讨论，复习巩固之前关于信号时域运算与分解的内容。

内容讲解设计：

内容：讨论:（1）信号与自身卷积的结果；（2）信号直流量分量求解
讲解方式：通过微信公众号+TEASOFT先进行搜集答案，在进行讲解
时间：5五分钟: 题目介绍与回答1分钟；题目讲解：4分钟
注意事项：第一小题详细讨论；第二小题简略；

（2）通过“数学虚幻模式”引入傅里叶变换性质

为了突出研究傅里叶变换性质的重要性，通过“ 数学虚幻模式 ”题目的讨论，设定一个悬念，引起对于傅里叶性质的兴趣。到课程结束时再进行复盘。

内容讲解设计：

内容：讨论 数学虚幻模式 内容，引入傅里叶变换性质分析。
讲解方式：通过公众号+TEASOFT先搜集同学意见；然后在给出求解思路。
时间：5分钟：3分钟讲解题目和搜集答案；2分钟简述求解思路；
注意事项：突出问题直接求解的难度，反映傅里叶变换可以将问题进行转换。

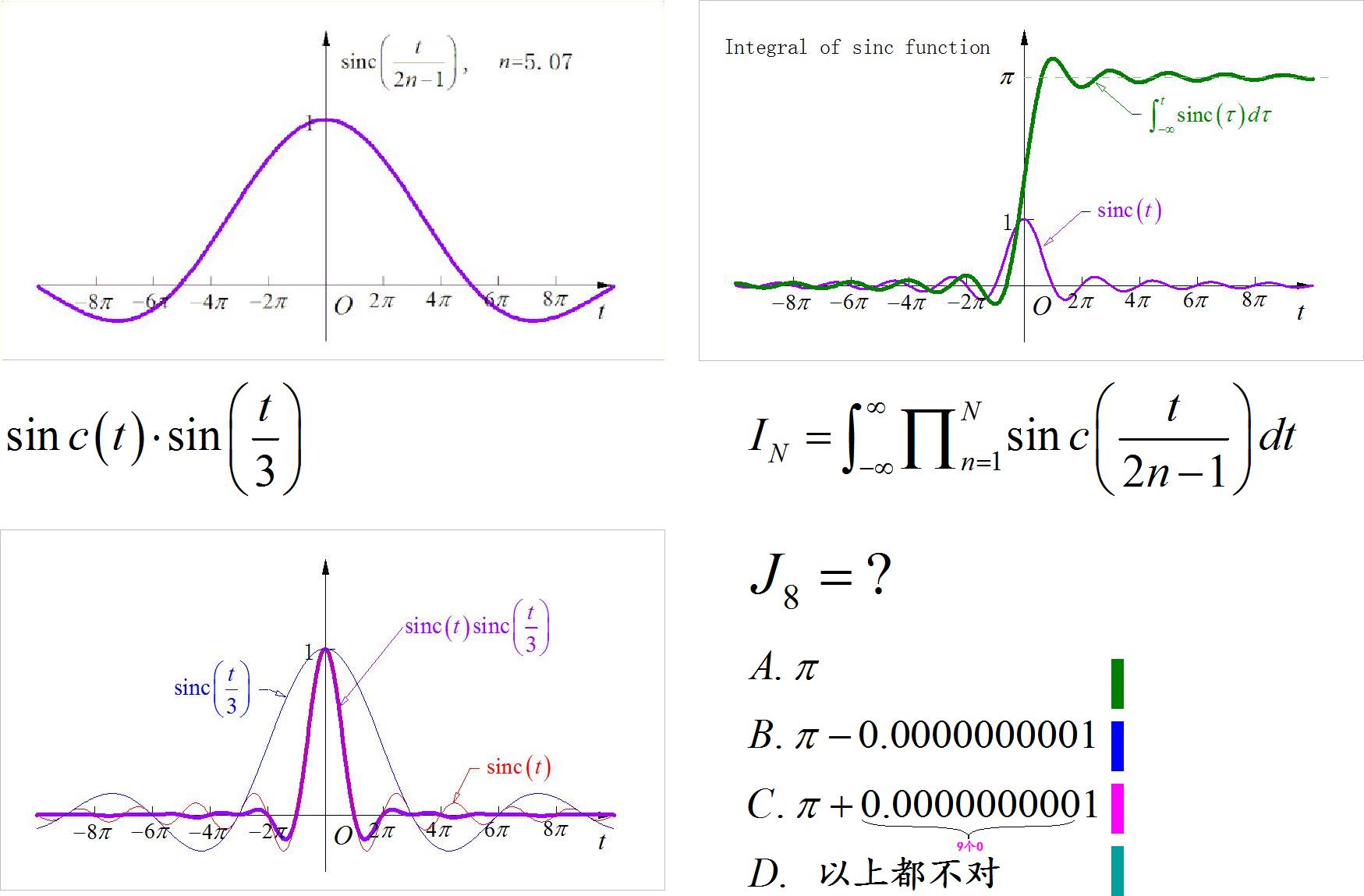
▲ 图2.2.2 “数学虚幻模式”问题介绍与问题讨论

^{▲ 图2.2.2 “数学虚幻模式”问题介绍与问题讨论}

（3）概况傅里叶变换性质

讲述傅里叶变换的丰富和多样，通过与信号在时域中的基本操作的对应，理解为何选择这些性质进行讨论；它们之间有什么杨的内在联系；

内容讲解设计：

内容：对于傅里叶变换性质进行综述；对比傅里叶变换与信号时域运行之间的对应关系；
讲解方式：通过课件进行讲解；
时间：5分钟；
注意事项：NULL

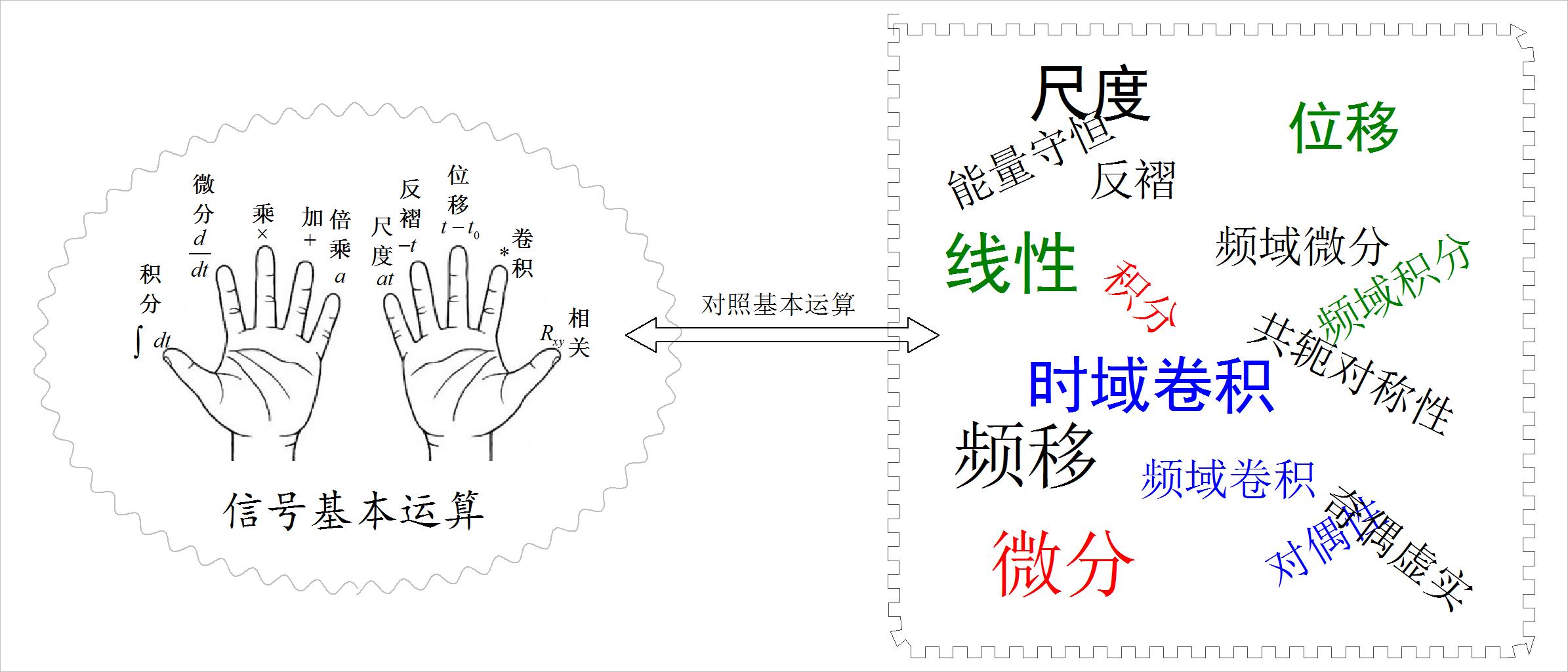
▲ 图2.3.1 傅里叶变换性质与信号基本运算

^{▲ 图2.3.1 傅里叶变换性质与信号基本运算}

（4）讲解傅里叶变换性质

这是此次课程的重点内容。按照课程前面讨论时间开销的情况下，在两堂课程剩下的时间内，确保讲述完傅里叶变换的线性特性、尺度特性、时移特性、频域特性。如果时间还有富余，可以讲完微分特性、积分特性。

内容讲解设计：

内容：讲解傅里叶变换主要特性。
讲解方式：安装课件安排的顺序完成主要性质的讲解。通过定义、证明、例题、应用等多个方面进行阐释。
时间：总时间为70分钟。平均每个性质讲解时间在10分钟到15分钟。
注意事项：（1）线性特性可以简略；（2）揭示时移与频域特性的对称关系；（3）根据时间进度，在微分特性与积分特性讲解中给出频域微分与积分特性对照。

（5）课程总结与问题复盘

对于本次课程中傅里叶变换讲解内容进行总结，对剩余的性质（卷积特性）进行引导介绍。复盘在课程第二环节（数学虚幻模式）遗留的问题，利用已经讲述的性质对其进行解释。

内容讲解设计：

内容：总结已经讲解的傅里叶变换性质；复盘数学虚幻模式问题分析。
讲解方式：口述总结；黑板推演；
时间：5分钟
注意事项：提示关于对数学虚幻模式的完整分析在课后通过微信推文给出。

3、教学条件准备

支撑这次课程中的主要条件包括：

用于课程讨论的微信+TEASOFT网络支撑环节；
基于TEASOFT软件的电子课件的准备；
对于大班的同学，需要提前通知注册微信公众号。

§03 课堂教学实施

根据前面备课中对于课程教学设计，在教学当日上午完成课堂教学。下面分为四个方面对于教学实施中的方式进行归纳。

1、讨论中鼓励与引导

（1）课前铺垫

作为早上第一大节（早上8:00钟）课程，相对其他时间阶段学生来从寝室与食堂到达教室的提前量较短，需要较长安顿时间。需要使用较长引导话语来给出本次课程主要内容与环节。由于需要使用微信平台与TEASOFT软件配合完成课堂讨论，提醒同学提前使用手机或者PAD进入公众号界面，并鼓励基极参与课堂讨论。

（2）问题讲解引导

在课程主题内容前的三个讨论互动话题中，都是采用先介绍问题，由同学通过手机回答，并由TEASOFT软件实时统计显示结果，根据同学给出答案统计进行问题展开。根据讨论话题的难易程度和作用，在讲解时间分配，话音引导方面要有区别。

作业习题卷积运算：这个题目需理解容易造成误区，容易形成大多数同学给出的答案是错误。介绍的时候尽量简短；在同学手机回复的过程中，给出求解思路提醒，此时会出现同学临时改变结果的情况。在大班讲解过程中这个情况非常明显。讲解过程中突出卷积图解发阶段划分在判断上的作用。
作业系统信号直流分量：这个题目较容易，是在上一题大多数出错的情况下的对同学们的一个鼓励。这个题目可以在学生手机回复与讲解合二为一，节省下时间留给下面讨论话题使用。

引导话题数学虚幻模式：这个题目内容比较复杂，需要花3分钟以上的时间，对于sinc函数的面积，sinc函数相乘之后积分以及特殊的积分序列进行介绍。为了达到数学模式突变带来的惊讶，内容讲解需要能够使得同学具有初步判断的能力。学生手机回复答案往往会集中在两个选择方面。在之后给出正确答案，并引出所需要使用到的基本性质。不需要讲解，留在课程结束时进行复盘。

2、揭示性质内部联系

进入傅里叶变换性质正式讲解过程，为了避免对性质种类多而产生“开中药部”的疲惫感觉，注意引导在揭示各个性质之间的内在逻辑关系。

傅里叶变换的时移特性与频移特性在实践中有着不同的应用背景，但在数学形式上则体现了时域与频域之间的平移与相位之间的对称关系，表达式上具有很强的相似性。
在微分定理与积分定理的讲解中，给出时域和频域这两个定理的不同形式；

对于性质定理的证明，除了在积分性质证明过程中进行详细讨论外，其它定理证明都不做详细讨论。只是汇总这些证明过程中的共性。这部分内容在课件备课中都进行了规划。

▲ 图3.2.1 对比时移与频移之间的内在逻辑关系

^{▲ 图3.2.1 对比时移与频移之间的内在逻辑关系}

3、举例详细与简略

揭示傅里叶变换背后的物理含义与实际应用是关节。作为第一次认知这些性质的同学，使用简单信号分析作为举例是非常重要的。这部分的教学经过多年的实践，所选择的举例以及相关联的解释都通过TEASOFT教学软件逐步进行课堂展示。

对于电子课件上的应用举例，对有着丰富应用对应背景的，求解过程涉及到技巧比较综合的进行详细分析。重点强调这些举例之间的所强调不同。一些例题可以提醒结合课后作业进行复习。

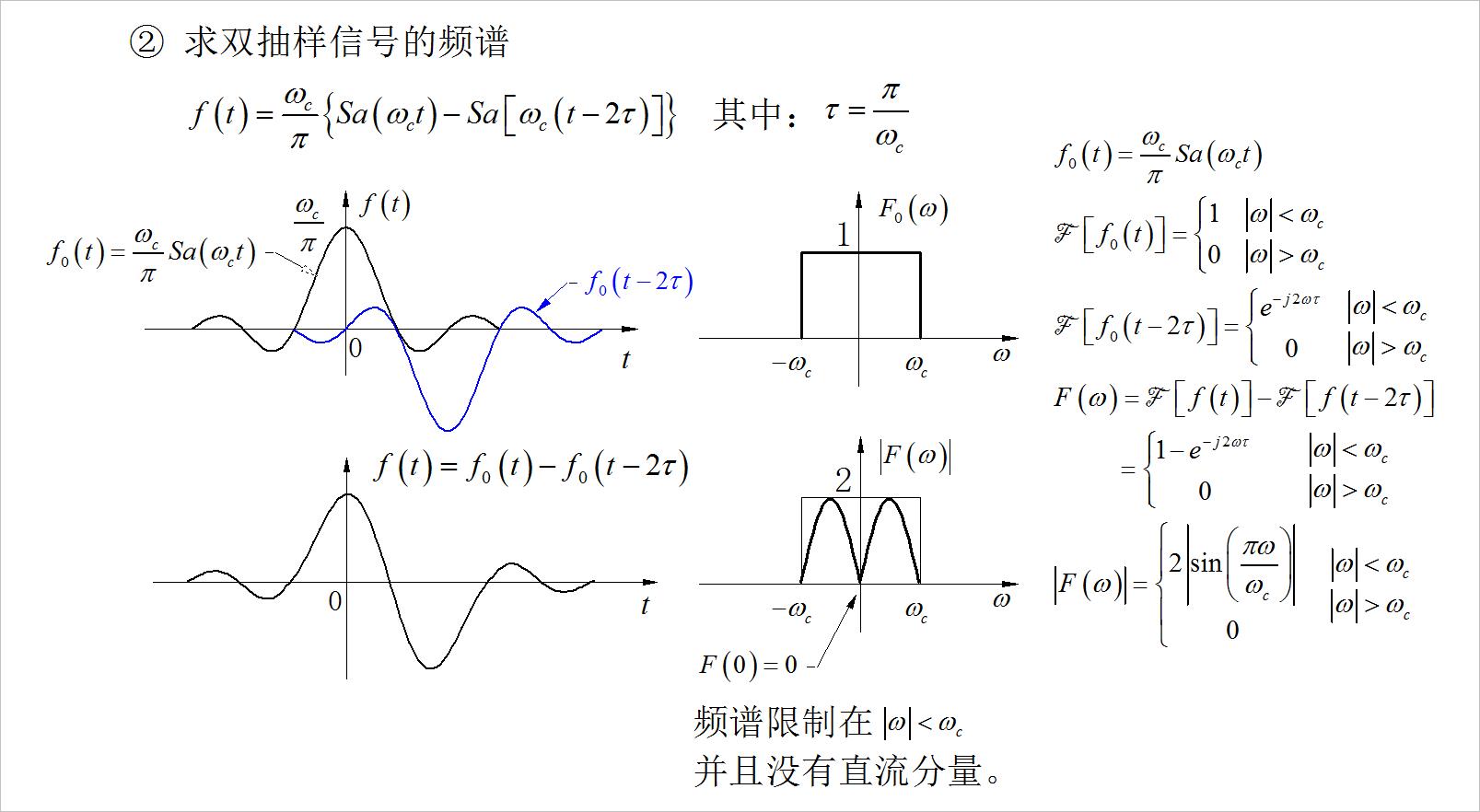
▲ 图3.3.1 详细讲解的信号频谱分析例题

^{▲ 图3.3.1 详细讲解的信号频谱分析例题}

4、问题复盘与引申

根据课程进展由剩余时间确定课程暂停的阶段。由于本课程在前面的引导部分，对于“数学虚幻模式”讨论留有悬疑，需要在课程结束前5分钟左右时间对于这个问题进行复盘。讲解本课程所使用的傅里叶变换性质在分析这个问题过程中的应用。并且指出留待下节课讲授的卷积定理是最终揭示问题答案全部细节的最后部分。

提醒课后给同学们推送的 从数学中的虚幻模式到傅里叶变换性质 中给出了本问题的详细解答。