(建议收藏)matlab在线性代数问题中的计算机求解进阶问题及解决方案集锦
Posted 文宇肃然
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了(建议收藏)matlab在线性代数问题中的计算机求解进阶问题及解决方案集锦相关的知识,希望对你有一定的参考价值。
前言
关于MATLAB系列的精品专栏大家可参见
喜欢的小伙伴可自行订阅,你的支持就是我不断更新的动力哟!
线性代数问题的计算机求解进阶01
问题:
Jordan 矩阵是矩阵分析中一类很实用的矩阵,其一般形式为
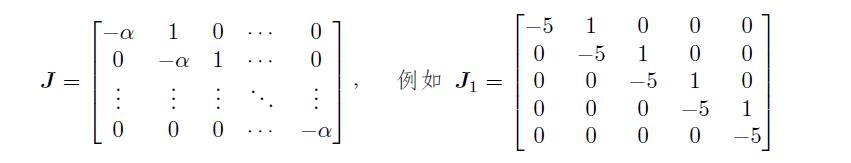
试利用diag() 函数给出构造J1 的语句。
解:
利用diag() 能够构造对角矩阵和次对角矩阵的性质,可以由下面语句建立起所需的矩阵。
>> J1=diag([-5 -5 -5 -5 -5])+diag([1 1 1 1],1)
J1 =
-5 1 0 0 0
0 -5 1 0 0
0 0 -5 1 0
0 0 0 -5 1
0 0 0 0 -5
拓展:
幂零矩阵是一类特殊的矩阵,其基本形式为:
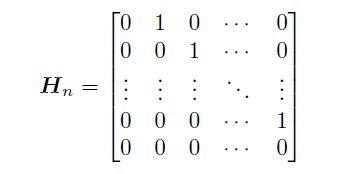
亦即,矩阵的次主对角线元素为1,其余均为0,试验证对指定阶次的幂零矩阵,有H^i_n= 0 对所有的 i > n 成立。
解:
可以用循环的方式构造出各阶幂零矩阵,并对其求出i + 1 次方,判定得出矩阵的范数,若发现范数大于0 的阶次,则显示其阶次,若为零矩阵则不显示任何内容。通过运行下面的语句,可见不显示任何内容,故 i < 100 的幂零矩阵满足上述性质。
>> for i=1:100
A=diag(ones(1,i),1);
if norm(A^(1+i))>0, disp(i); end
end
拓展:
试从矩阵的显示格式区分符号矩阵和数值矩阵,明确它们的含义和应用场合。若A 矩阵为数值矩阵,B 为符号矩阵,C=A*B 运算得出的C 矩阵是符号矩阵还是数值矩阵?
解:
得出的结果当然是符号矩阵,见下例。
>> A=ones(5);
B=sym(A);
A*B
ans =
[ 5, 5, 5, 5, 5]
[ 5, 5, 5, 5, 5]
[ 5, 5, 5, 5, 5]
[ 5, 5, 5, 5, 5]
[ 5, 5, 5, 5, 5]
线性代数问题的计算机求解进阶02
问题:
请将下面给出的矩阵A 和B 输入到MATLAB 环境中,并将它们转换成符号矩阵。
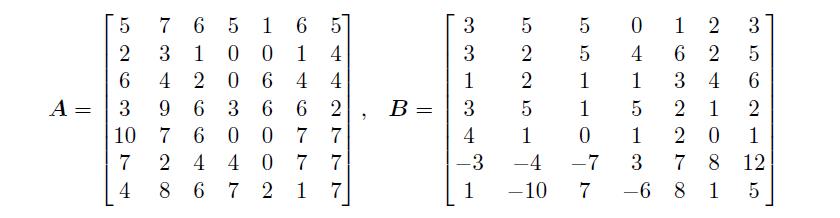
解:
矩阵的输入与转换是很直接的。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2;
10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7];
A=sym(A)
A =
[ 5, 7, 6, 5, 1, 6, 5]
[ 2, 3, 1, 0, 0, 1, 4]
[ 6, 4, 2, 0, 6, 4, 4]
[ 3, 9, 6, 3, 6, 6, 2]
[ 10, 7, 6, 0, 0, 7, 7]
[ 7, 2, 4, 4, 0, 7, 7]
[ 4, 8, 6, 7, 2, 1, 7]
>> B=[3,5,5,0,1,2,3; 3,2,5,4,6,2,5; 1,2,1,1,3,4,6; 3,5,1,5,2,1,2;
4,1,0,1,2,0,1; -3,-4,-7,3,7,8,12; 1,-10,7,-6,8,1,5];
B=sym(B)
B =
[ 3, 5, 5, 0, 1, 2, 3]
[ 3, 2, 5, 4, 6, 2, 5]
[ 1, 2, 1, 1, 3, 4, 6]
[ 3, 5, 1, 5, 2, 1, 2]
[ 4, 1, 0, 1, 2, 0, 1]
[ -3, -4, -7, 3, 7, 8, 12]
[ 1, -10, 7, -6, 8, 1, 5]
拓展:
试求出Vandermonde 矩阵

的行列式,并以最简的形式显示结果。
解:
利用书中编写的面向符号矩阵的vander() 函数,可以构造出Vandermonde 矩阵并可以求出该矩阵的行列式。
>> syms a b c d e;
A=vander([a b c d e])
A =
[ a^4, a^3, a^2, a, 1]
[ b^4, b^3, b^2, b, 1]
[ c^4, c^3, c^2, c, 1]
[ d^4, d^3, d^2, d, 1]
[ e^4, e^3, e^2, e, 1]
>> det(A),
simple(ans)
ans =
(c-d)*(b-d)*(b-c)*(a-d)*(a-c)*(a-b)*(-d+e)*(e-c)*(e-b)*(e-a)
线性代数问题的计算机求解进阶03
问题:
利用MATLAB 语言提供的现成函数对两个矩阵
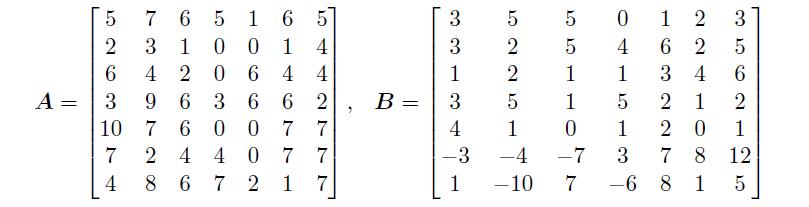
进行分析,判定它们是否为奇异矩阵,得出矩阵的秩、行列式、迹和逆矩阵,检验得出的逆矩阵是否正确。
解:
以A 矩阵为例,可以对其进行如下分析。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2;
10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7];
A=sym(A);
rank(A)
ans =
7
>> det(A)
ans =
-35432
>> trace(A)
ans =
27
>> B=inv(A);
latex(B)
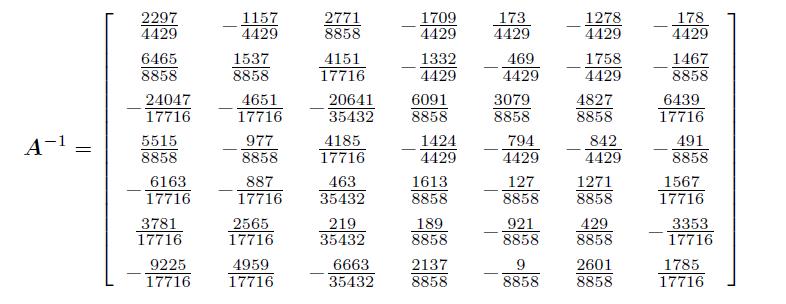
>> A*B
ans =
[ 1, 0, 0, 0, 0, 0, 0]
[ 0, 1, 0, 0, 0, 0, 0]
[ 0, 0, 1, 0, 0, 0, 0]
[ 0, 0, 0, 1, 0, 0, 0]
[ 0, 0, 0, 0, 1, 0, 0]
[ 0, 0, 0, 0, 0, 1, 0]
[ 0, 0, 0, 0, 0, 0, 1]
拓展:
试求出A 和B 矩阵的特征多项式、特征值与特征向量,并验证Hamilton-Caylay 定理,解释并验证如何运算能消除误差。
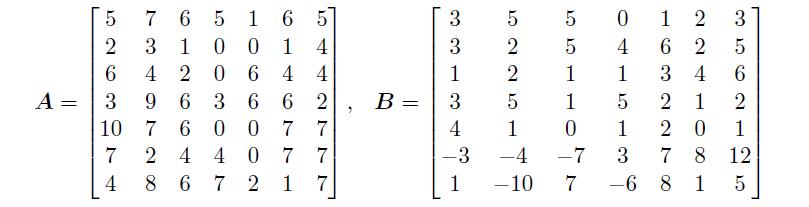
解:
仍以A 矩阵为例。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2;
10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7];
A=sym(A);
eig(A)
ans =
5.0093966800793665262158730069552
28.679593193974410579078264020229
.27480714110743938760483528351799e-1+1.1755376247101009492093136044131*i
-1.6336795424500642956747726147329+6.9740721596526560301948635104611*i
-3.4765922173751363914655588544224
-1.6336795424500642956747726147329-6.9740721596526560301948635104611*i
.27480714110743938760483528351799e-1-1.1755376247101009492093136044131*i
>> p=poly(A)
p =
x^7-27*x^6-18*x^5-1000*x^4+3018*x^3+24129*x^2+2731*x+35432
>> p=sym2poly(p)
p =
1 -27 -18 -1000 3018 24129 2731 35432
>> polyvalm(p,A)
ans =
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
[ 0, 0, 0, 0, 0, 0, 0]
拓展:
试对上一例中给出的A 和B 矩阵进行奇异值分解、LU 分解及正交分解矩阵。
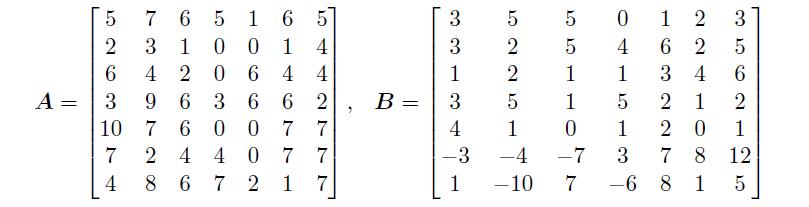
解:
仍以A 矩阵为例,这里只考虑数值解。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2;
10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7];
[s,v,d]=svd(A)
s =
-0.4239 -0.1061 0.2030 -0.4091 -0.0746 0.0576 0.7691
-0.1481 0.0894 0.0836 0.4027 -0.2052 0.8703 0.0378
-0.2974 0.0356 -0.5776 0.4840 0.4829 -0.1222 0.3069
-0.3982 -0.5760 -0.4427 -0.3445 -0.0925 0.1884 -0.3884
-0.4894 0.4970 -0.1564 0.0971 -0.6067 -0.3010 -0.1447
-0.3790 0.4736 0.2221 -0.3276 0.5799 0.1683 -0.3328
-0.4101 -0.4200 0.5902 0.4480 0.0790 -0.2644 -0.1739
v =
32.4615 0 0 0 0 0 0
0 9.3091 0 0 0 0 0
0 0 7.8637 0 0 0 0
0 0 0 4.8206 0 0 0
0 0 0 0 4.4123 0 0
0 0 0 0 0 1.6953 0
0 0 0 0 0 0 0.4135
d =
-0.4492 0.5090 -0.1602 0.2281 0.0328 -0.6071 0.3028
-0.4821 -0.4781 -0.0702 0.1634 -0.5653 0.1976 0.3857
-0.3878 -0.1693 0.1248 -0.2472 -0.2468 -0.3642 -0.7421
-0.2372 -0.3550 0.5985 -0.2601 0.5035 -0.1915 0.3188
-0.1669 -0.4500 -0.6026 0.2746 0.5497 -0.0438 -0.1643
-0.3931 0.2700 -0.3325 -0.6947 0.1394 0.3917 0.0807
-0.4204 0.2869 0.3491 0.4842 0.2081 0.5173 -0.2714
>> [L U]=lu(A)
L =
0.5000 0.5072 0.5556 0.1099 0.5000 0.5376 1.0000
0.2000 0.2319 -0.7500 0.6429 0.5702 1.0000 0
0.6000 -0.0290 -0.9444 1.0000 0 0 0
0.3000 1.0000 0 0 0 0 0
1.0000 0 0 0 0 0 0
0.7000 -0.4203 1.0000 0 0 0 0
0.4000 0.7536 0.2778 0.6484 1.0000 0 0
U =
10.0000 7.0000 6.0000 0 0 7.0000 7.0000
0 6.9000 4.2000 3.0000 6.0000 3.9000 -0.1000
0 0 1.5652 5.2609 2.5217 3.7391 2.0580
0 0 0 5.0556 8.5556 3.4444 1.7407
0 0 0 0 -8.7692 -8.0110 2.5751
0 0 0 0 0 3.8534 1.5794
0 0 0 0 0 0 -1.9204
>> orth(A)
ans =
-0.4239 -0.1061 0.2030 -0.4091 -0.0746 0.0576 0.7691
-0.1481 0.0894 0.0836 0.4027 -0.2052 0.8703 0.0378
-0.2974 0.0356 -0.5776 0.4840 0.4829 -0.1222 0.3069
-0.3982 -0.5760 -0.4427 -0.3445 -0.0925 0.1884 -0.3884
-0.4894 0.4970 -0.1564 0.0971 -0.6067 -0.3010 -0.1447
-0.3790 0.4736 0.2221 -0.3276 0.5799 0.1683 -0.3328
-0.4101 -0.4200 0.5902 0.4480 0.0790 -0.2644 -0.1739
拓展:
试求出下面矩阵的特征值、特征向量、奇异值。
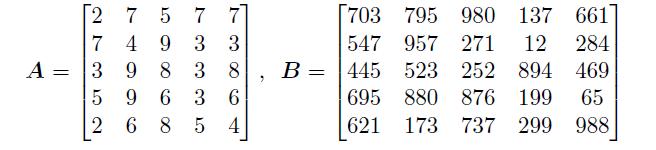
解:
A 矩阵的分析如下。
>> A=[2,7,5,7,7; 7,4,9,3,3; 3,9,8,3,8; 5,9,6,3,6; 2,6,8,5,4]
B=[703,795,980,137,661; 547,957,271,12,284; 445,523,252,894,469;
695,880,876,199,65; 621,173,737,299,988]
[e,f]=eig(A)
e =
0.4452 0.5756 0.3203 - 0.3633i 0.3203 + 0.3633i -0.0706
0.4256 0.1987 -0.5697 -0.5697 0.6063
0.4933 -0.5629 -0.0168 + 0.0797i -0.0168 - 0.0797i -0.4901
0.4607 0.5010 -0.0594 + 0.3503i -0.0594 - 0.3503i -0.5229
0.4062 -0.2478 0.5457 - 0.1010i 0.5457 + 0.1010i 0.3373
f =
27.8629 0 0 0 0
0 2.6062 0 0 0
0 0 -2.2306 + 1.8926i 0 0
0 0 0 -2.2306 - 1.8926i 0
0 0 0 0 -5.0078
>> svd(A)
ans =
28.7819
6.5830
4.2345
2.6949
1.4393
线性代数问题的计算机求解进阶04
问题:
试判定下面矩阵是否为正定矩阵,如是,则得出其Cholesky 分解矩阵。
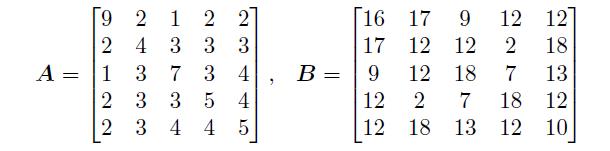
解:
A 矩阵能进行Cholesky 分解,故为正定矩阵。
>> A=[9,2,1,2,2; 2,4,3,3,3; 1,3,7,3,4; 2,3,3,5,4; 2,3,4,4,5];
chol(A)
ans =
3.0000 0.6667 0.3333 0.6667 0.6667
0 1.8856 1.4731 1.3553 1.3553
0 0 2.1723 0.3596 0.8200
0 0 0 1.6092 0.8848
0 0 0 0 1.1240
B 矩阵进行Cholesky 分解失败,故为非正定矩阵。
>> B=[16,17,9,12,12; 17,12,12,2,18; 9,12,18,7,13; 12,2,7,18,12; 12,18,13,12,10];
chol(B)
??? Error using ==> chol
Matrix must be positive definite.
拓展:
试对矩阵
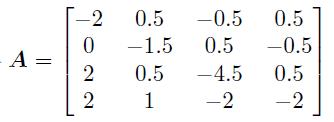
进行Jordan 变换,并得出变换矩阵。
解:
将A 输入,并转换成符号矩阵,这样就能得出Jordan 变换矩阵与Jordan 矩阵。
>> A=[-2,0.5,-0.5,0.5; 0,-1.5,0.5,-0.5; 2,0.5,-4.5,0.5; 2,1,-2,-2];
[V J]=jordan(sym(A))
V =
[ 0, 1/2, 1/2, -1/4]
[ 0, 0, 1/2, 1]
[ 1/4, 1/2, 1/2, -1/4]
[ 1/4, 1/2, 1, -1/4]
J =
[ -4, 0, 0, 0]
[ 0, -2, 1, 0]
[ 0, 0, -2, 1]
[ 0, 0, 0, -2]
线性代数问题的计算机求解进阶05
问题:
试求下面齐次方程的基础解系。
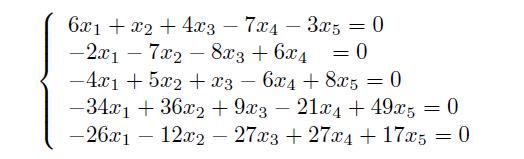
解:
可以将方程写成矩阵形式,得出的两列向量为方程的基础解系。
>> A=[6,1,4,-7,-3; -2,-7,-8,6,0; -4,5,1,-6,8; -34,36,9,-21,49; -26,-12,-27,27,17];
A=sym(A);
rank(A)
ans =
3
>> null(A)
ans =
[ 191/34, 95/17]
[ 0, 1]
[ 1, 0]
[ 109/34, 103/34]
[ 173/34, 151/34]
拓展:
试求下面线性代数方程的解析解与数值解,并检验解的正确性。
解:求出A, [A;B] 两个矩阵的秩,可见二者相同,所以方程不是矛盾方程,应该有无穷多解。
>> A=[2,-9,3,-2,-1; 10,-1,10,5,0; 8,-2,-4,-6,3; -5,-6,-6,-8,-4];
B=[-1,-4,0; -3,-8,-4; 0,3,3; 9,-5,3];
[rank(A), rank([A B])]
ans =
4 4
用下面的语句可以求出方程的解析解,并可以验证该解没有误差。
>> x0=null(sym(A));
x_analytical=sym(A)\\B;
syms a;
x=a*[x0 x0 x0]+x_analytical
x =
[ a+967/1535, a-943/1535, a-159/1535]
[ -1535/1524*a, -1535/1524*a, -1535/1524*a]
[ -3659/1524*a-1807/1535,-3659/1524*a-257/1535,-3659/1524*a-141/1535]
[ 1321/508*a+759/1535, 1321/508*a-56/1535, 1321/508*a-628/1535]
[ -170/127*a-694/307, -170/127*a+719/307, -170/127*a+103/307]
>> A*x-B
ans =
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
用数值解方法也可以求出方程的解,但会存在误差,且与任意常数a 的值有关。
>> x0=null(A);
x_numerical=A\\B;
syms a;
x=a*[x0 x0 x0]+x_numerical;
vpa(x,10)
ans =
[ .2474402553*a+.1396556436, .2474402553*a-.6840666849, .2474402553*a-.1418420333]
[-.2492262414*a+.4938507789,-.2492262414*a+.7023776988e-1,-.2492262414*a+.3853511888e-1]
[ -.5940839201*a, -.5940839201*a, -.5940839201*a]
[ .6434420813*a-.7805411315, .6434420813*a-.2178190763,.6434420813*a-.5086089095]
[-.3312192394*a-1.604263460, -.3312192394*a+2.435364854, -.3312192394*a+.3867176824]
>> A*x-B
ans =
[ 1/18014398509481984*a, 1/18014398509481984*a, 1/18014398509481984*a]
[ -5/4503599627370496*a, -5/4503599627370496*a, -5/4503599627370496*a]
[ -25/18014398509481984*a, -25/18014398509481984*a, -25/18014398509481984*a]
[ 13/18014398509481984*a, 13/18014398509481984*a, 13/18014398509481984*a]
试判定下面的线性代数方程是否有解。
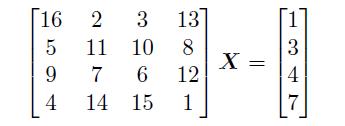
解:
由秩判定矩阵可以得出如下结果。
>> A=[16,2,3,13; 5,11,10,8; 9,7,6,12; 4,14,15,1];
B=[1; 3; 4; 7];
[rank(A), rank([A B])]
ans =
3 4
由得出的结果看,A, [A;B] 两个矩阵的秩不同,故方程是矛盾方程,没有解。
拓展:
试求出线性代数方程的解析解,并验证解的正确性。

解:先判定方程解的存在性,得出结论,方程有无穷多解。
>> A=[2,9,4,12,5,8,6; 12,2,8,7,3,3,7; 3,0,3,5,7,5,10; 3,11,6,6,9,9,1;
11,2,1,4,6,8,7; 5,-18,1,-9,11,-1,18; 26,-27,-1,0,-15,-13,18];
X=[1,9; 5,12; 4,12; 10,9; 0,5; 10,18; -20,2];
[rank(A), rank([A X])]
ans =
5 5
这样就能解出方程的解析解,并验证方程解是这正确的。
>> x0=null(sym(A)); syms a1 a2;
x1=sym(A)\\X;
x=a1*[x0(:,1) x0(:,1)]+a2*[x0(:,2) x0(:,2)]+x1
x =
[ 6386/9453*a1-7118/9453*a2-10519/37810, 6386/9453*a1-7118/9453*a2-2159/7562]
[ a1+17927/18905, a1+1397/3781]
[-14446/9453*a1+15643/9453*a2+25857/18905,-14446/9453*a1+15643/9453*a2+4691/3781]
[ 6437/9453*a1-15716/9453*a2-54143/37810, 6437/9453*a1-15716/9453*a2-3527/7562]
[ 16855/9453*a1-24190/9453*a2, 16855/9453*a1-24190/9453*a2]
[ -25198/9453*a1+25561/9453*a2, -25198/9453*a1+25561/9453*a2]
[ a2+29837/37810, a2+8671/7562]
>>A*x-X
ans =
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
[ 0, 0]
拓展:
试用数值方法和解析方法求取下面的Sylvester 方程,并验证得出的结果。
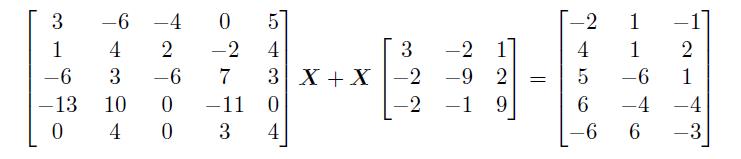
解:
用下面的语句可以直接求出其数值解,并可以判定该解的精度。
>> A=[3,-6,-4,0,5; 1,4,2,-2,4; -6,3,-6,7,3; -13,10,0,-11,0; 0,4,0,3,4];
B=[3,-2,1; -2,-9,2; -2,-1,9];
C=[-2,1,-1; 4,1,2; 5,-6,1; 6,-4,-4; -6,6,-3];
X=lyap(A,B,C)
X =
-4.0569 -14.5128 1.5653
0.0356 25.0743 -2.7408
9.4886 25.9323 -4.4177
2.6969 21.6450 -2.8851
7.7229 31.9100 -3.7634
>> norm(A*X+X*B+C)
ans =
2.7917e-013
利用书中给出的解析解方法,可以求出该方程的解析解。
>> X=lyap(sym(A),B,C)
X =
[-434641749950/107136516451,-4664546747350/321409549353, 503105815912/321409549353]
[ 3809507498/107136516451, 8059112319373/321409549353, -880921527508/321409549353]
[1016580400173/107136516451, 8334897743767/321409549353,-1419901706449/321409549353]
[ 288938859984/107136516451, 6956912657222/321409549353, -927293592476/321409549353]
[827401644798/107136516451,10256166034813/321409549353,-1209595497577/321409549353]
>> A*X+X*B+C
ans =
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
[ 0, 0, 0]
线性代数问题的计算机求解进阶06
问题:

解:
可以容易地得出该Riccati 方程的数值解,并可见精度可以达到10¡13 级。
>> A=[-27,6,-3,9; 2,-6,-2,-6; -5,0,-5,-2; 10,3,4,-11];
B=[0,3; 16,4; -7,4; 9,6];
Q=[6,5,3,4; 5,6,3,4; 3,3,6,2; 4,4,2,6];
R=[4,1; 1,5];
C=Q;
B=B*inv(R)*B';
X=are(A,B,C)
X =
0.12263582711547 0.10884608244578 0.02726560429376 0.11845697768205
0.10884608244578 0.28127417024552 0.16587415559524 0.06370964357824
0.02726560429376 0.16587415559524 0.40229938956082 0.01389200165902
0.11845697768205 0.06370964357824 0.01389200165902 0.22086908688248
>> norm(A'*X+X*A-X*B*X+C)
ans =
3.142051364911015e-014
拓展:

解:
用下面的语句可以求出矩阵问题的解析解。
>> A1=diag([-3 -3 -3])+diag([1 1],1);
A2=[-5 1; 0 -5];
A3=diag([-1 -1 -1 -1])+diag([1 1 1],1);
A=sym(diagm(A1,A2,A3));
>> syms t; expm(A*t)
可以用LATEX 将其显示成
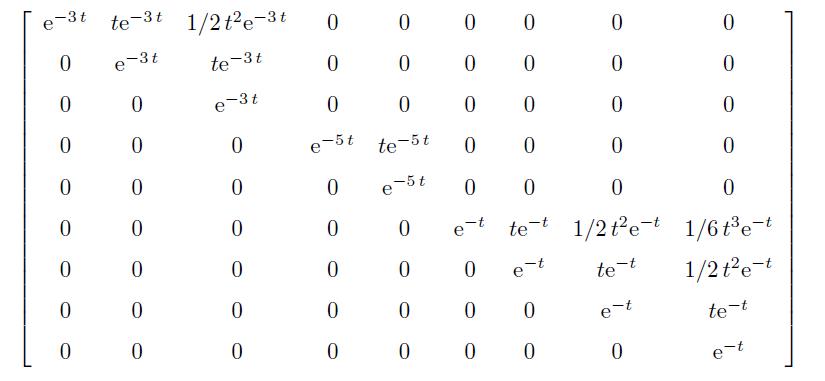
其他矩阵函数可以由下面的语句求出,限于篇幅,不列出具体结果。
>> syms x t; funm(A,'sin(2*x*t+sym(pi)/3)',x)
funm(A,'exp(x^2*t)*x^2+sin(x^3*t)*x*t+exp(sin(x*t))',x)
例如可以求出上述结果的第一行第二列元素为
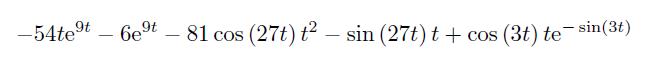

解:
用下面的语句可以直接得出矩阵指数解析解。
>> A=[-4.5,0,0.5,-1.5; -0.5,-4,0.5,-0.5; 1.5,1,-2.5,1.5; 0,-1,-1,-3];
A=sym(A);
syms t;
expm(A*t)
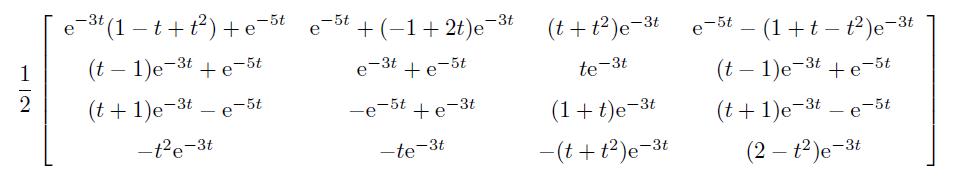
可以得出其他矩阵函数。
>> syms x t; funm(A,'sin(x*t)',x)
syms x t; funm(A,'exp(x*t)*sin(x^2*exp(x*t)*t)',x)
以上是关于(建议收藏)matlab在线性代数问题中的计算机求解进阶问题及解决方案集锦的主要内容,如果未能解决你的问题,请参考以下文章