算法：62唯一路径Unique Paths 动态规划和排列组合算法

Posted 2021-06-28 架构师易筋

62. Unique Paths

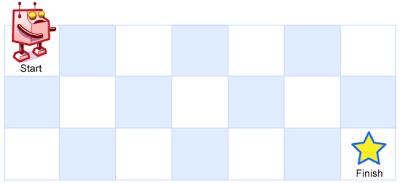
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Above is a 7 x 3 grid. How many possible unique paths are there?

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
   ​

Example 2:

Input: m = 7, n = 3
Output: 28

Constraints:

1 <= m, n <= 100

It’s guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

1 排列组合解法

这是一个组合问题，可以在没有 DP 的情况下解决。对于 mxn 网格，机器人必须准确地向下移动 m-1 步和向右移动 n-1 步，这些可以以任何顺序完成。

例如，给出的问题是 3x7 矩阵，机器人需要以任意顺序执行 2+6 = 8 步，其中 2 步向下，6 步向右。那不过是一个排列问题。向下表示为“D”，向右表示为“R”，以下是路径之一：-

DRRRDRRR

我们必须告诉上面给定单词的排列总数。因此，将 m & n 都减少 1 并应用以下公式：-

总排列 = (m+n)！/（m！* n！）

以下是我的代码做同样的事情：-

class Solution {
    public int uniquePaths(int m, int n) {
        // permulation: (m + n)! / (m! * n!)
        if (m == 1 || n == 1) return 1;
        m--;
        n--;
        // switch m is big
        if (m < n) {
            n = m + n;
            m = n - m; // n
            n = n - m; // m
        }
        int j = 1;
        long sum = 1;
        for (int i = m + 1; i <= m + n; i++, j++) {
            sum = sum * i;
            sum = sum / j;
        }
        
        return (int)sum;
    }
}

2 动态规划解法 – 之前的文章

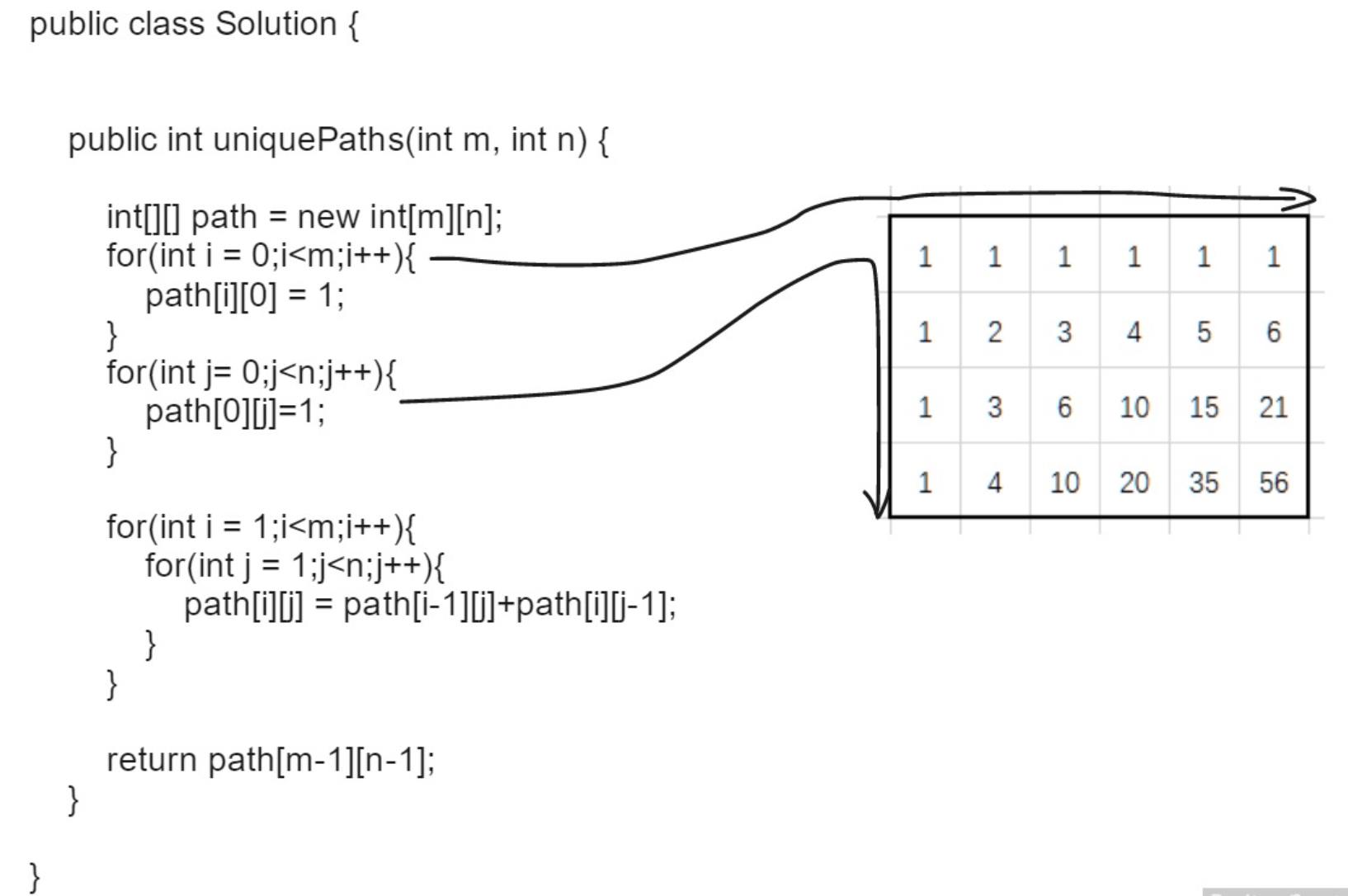
动态规划主要是找到跟上一条记录联系的公式，这里的公式就是path[i][j] = path[i-1][j] + path[i][j-1]。可以看下面的图，

1. 往下走的列path[i][0]都初始化为1，表示一直往下有一种的解法；往右走的行path[0][j]都初始化为1，表示一直往右有一种的解法。

2. 再看第二列，当前位置的记录是由上面的解法，和左边的解法，加起来就是当前的解法。所以 2 = 1 + 1， 3 = 2 + 1. 以此类推。

3. 结果是path[m-1][n-1], 因为是从0开始计算的。
   

public int uniquePaths(int m, int n) {
    int[][] dp = new int[m][n];
    for (int i = 0 ; i < m; i++) {
      dp[i][0] = 1;
    }
    for (int k = 0; k < n; k++) {
      dp[0][k] = 1;
    }
    for (int i = 1; i < m; i++) {
      for (int k = 1; k < n; k++) {
        dp[i][k] = dp[i - 1][k] + dp[i][k - 1];
      }
    }
​
    return dp[m - 1][n - 1];
  }

参考

https://leetcode.com/problems/unique-paths/discuss/22958/Math-solution-O(1)-space