数据结构——平衡二叉树(AVL树)

Posted 2021-06-28 两片空白

文章目录

• 前言
• 一.定义
• 二.基本操作
• • 1.查找，删除
  • 2.插入(如何调整)
  • • 如何调整
    • 代码实现插入

前言

首先我们来思考一下一个普通二叉树保存数据，如果想查找一个数据，由于普通二叉树保存数据是随机的，要找到数据的时间复杂度为O(n)。后面为了方便
，我们又学习二叉搜索树，它的定义是将比根节点小的数放左边，比根节点大的数放右边，并且每一课子树都是二叉搜索树这样使得数据在树上存储有一定
的规律，在一定情况下查找起来很方便。但是，二叉搜索数当给出数据的顺序不同时，二叉搜索树也会不同。比如如果给出的序列为{1，2，3，4，5}或
{3，2，1，4，5}两颗二叉搜索树会截然不同，查找效率也会不同。

我们知道一颗树的查找效率与树的高度有关，最好的树结构当然是满二叉树或者是完全二叉树，我们称这种树是平衡的。由我们知道二叉搜索树在一定情况下可以达到很好的查找效率。但是，通常情况二叉搜索树的结点插入顺序并不能事先确定，动态查找(查找时同时进行删除与插入操作)的时候总还是会改变数的结构，不能做到平衡。所以，我们就需要考虑如何保证既能完成动态查找，又能保持一个较完美树结构的二叉搜索树。这样我们就有两个问题需要考虑：一个是标准，什么样的树才是一颗树结构好的树，第二是平衡化处理，怎样使其达到平衡。

一.定义

平衡二叉树又称AVL树(由发明它的两位数学家名字命名)，它仍然是一颗二叉搜索树，所以具备二叉搜索树的所有性质，只是加上了"平衡"的限制。
平衡二叉树要不是一颗空树，要不是具备以下条件的非空二叉搜索树：
1. 左右子树高度差的绝对值不能超过1(平衡因子，相当于一种标准)。
2. 左右子树仍然是一颗平衡二叉树。
有了平衡因子的定义，我们就可以找出不平衡的树，然后再对其进行平衡化处理，处理的具体内容分如下。处理完后使树的高度能保持在O(logn)级别，使得
查找操作的时间复杂度为O(logn).

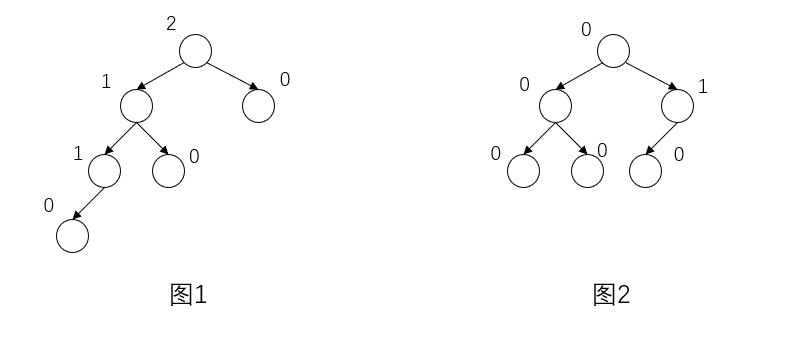
图1图2圆上为平衡因子的值，明显图1不是平衡二叉树，有提个点的平衡因子超过了1。图2是平衡二叉树。

二.基本操作

1.查找，删除

由于平衡二叉树仍是一颗二叉搜索树，其删除与查找操作并不会增加平衡因子，所以与二叉搜索树的操作相同。可见博客：二叉搜索树的查找与删除。

2.插入(如何调整)

如何调整

假设这里有一颗平衡二叉树：(上方代表平衡因子)

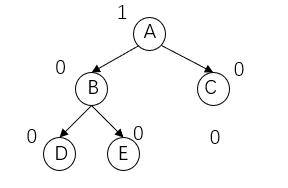
LL型
当要往D的左子树或者右子树插入结点时，此时破坏了原来平衡二叉树的平衡结构，如图：此时A结点的平衡因子超过了1，我们称A结点为发现问题结点，六角星为产生问题结点。

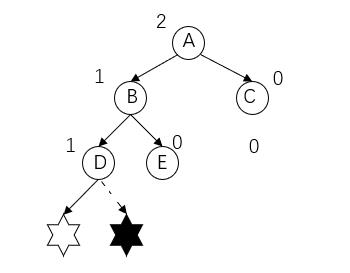
此时，我们需要看发现问题结点与产生问题结点路径上，从发现问题结点开始的连续三个结点。入上图的A->B->D。我们发现这三个结点都在发现问题结点A左子树的左子树上，我们称这种不平衡状态为LL型(向左倾斜)不平衡。
如何调整，LL型不平衡的调整策略主要将这三个结点(A,B,D)顺时针旋转，并且仍然要是一颗二叉搜索树。
由于二叉搜索树的性质：

1. 将B结点的右子树成为A的左子树。(B的左子树比B大，比A小)
2. 让A成为B的右子树(A比B大)
3. 将根节点设为B
   
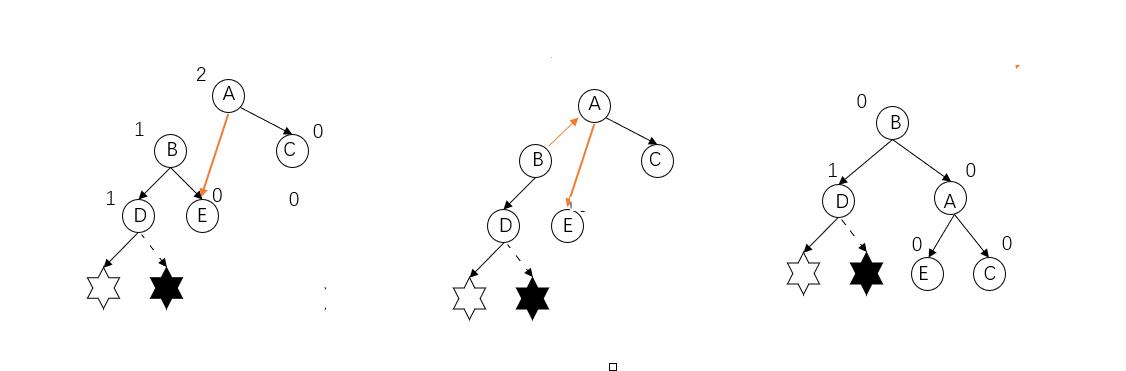
   显然只有只有从根节点到插入结点路径上的结点才会发生平衡因子的变化，因此只需要对这条路径上的失衡的结点进行调整，并且只需要把最靠近插入节点的失衡节点调整到正常，路径上的所有结点都会平衡。所以发现问题的结点不一定是根节点
   注意：看的是发现问题结点到产生问题结点路径上，从发现问题结点开始的连续三个结点的方向，确定是什么型。并且主要也是调整这三个结点。
   代码如下：

void SigelleftCir(Bactree **tree){//LL旋转
	Bactree *temp = NULL;
	temp = (*tree)->left;
	(*tree)->left = temp->right;
	temp->right = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//调整后要保持每个结点高度正确。
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp; //要赋值给(*tree),不然temp才是正确的树

}

RR型
RR型的处理方法与LL型类似，如图：

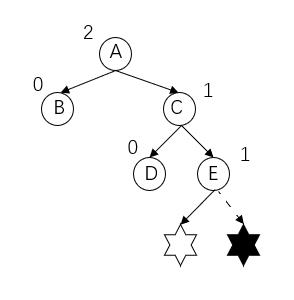
产生问题结点为六角星结点(插入E的左子树或者右子树)，发现问题结点为A结点。路径上从发现问题结点开始的连续三个结点为(A,C,E)结点，分别在发现问题结点右子树的右子树上，所以为RR型(向右倾斜)不平衡。
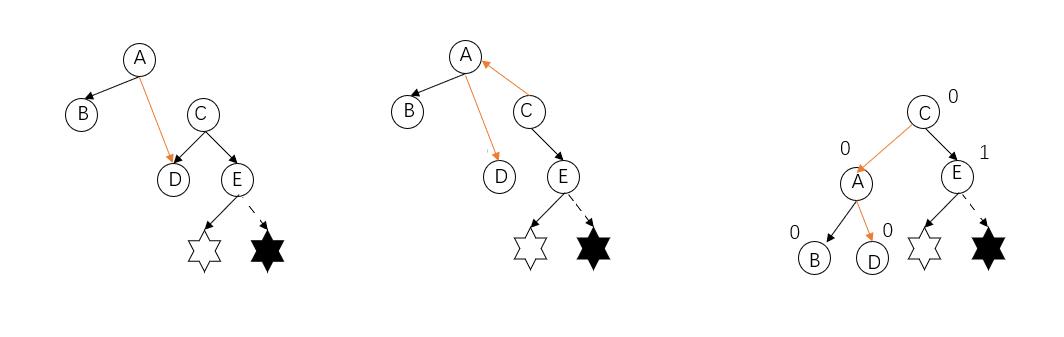
调整方式：主要将这三个结点(A,C,E)逆时针旋转，并且仍然要是一颗二叉搜索树。

1. 将C结点的左子树成为A的右子树。
2. 让A成为C的左子树
3. 将根节点设为C
   

void SigelrightCir(Bactree **tree){//RR旋转，与LL一样
	Bactree *temp = NULL;
	temp = (*tree)->right;
	(*tree)->right = temp->left;
	temp->left = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp;

LR型

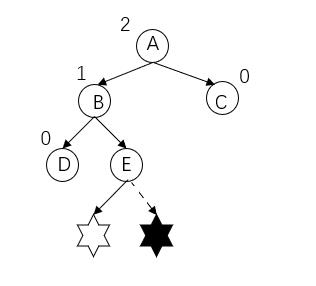
产生问题结点为六角星(插入E的左子树或者右子树)，发现问题结点为A结点。路径上从发现问题结点开始的连续三个结点为(A,B,E)结点，分别在发现问题结点左子树的右子树上，所以为LR型不平衡。
调整方式：“左-右双旋”，主要先将B结点作为根节点逆时针旋转(左旋)，再以A结点作为根节点顺时针旋转(右旋)。(画图以白色六角星作为插入)

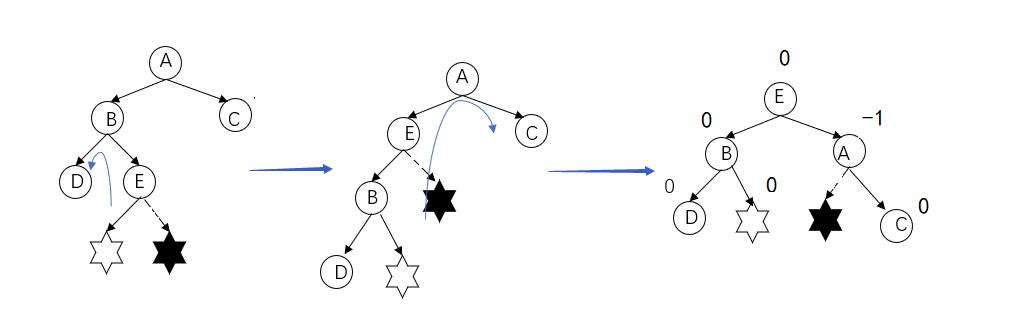
代码实现调整LR型就很简单了，先右旋，再左旋

void LeftrightCir(Bactree **tree){//LR旋转
	SigelrightCir(&((*tree)->left));
	SigelleftCir(tree);
}

RL型

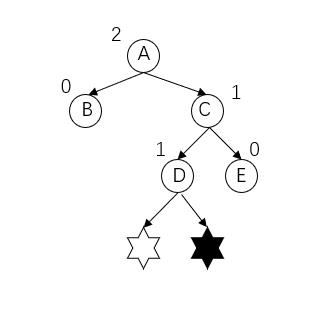
产生问题结点为六角星(插入D的左子树或者右子树)，发现问题结点为A结点。路径上从发现问题结点开始的连续三个结点为(A,C,D)结点，分别在发现问题结点右子树的左子树上，所以为RL型不平衡。
调整方式："右-左双旋"主要先将C结点作为根节点顺时针旋转(右旋)，再以A结点作为根节点逆时针旋转(左旋)。(画图以白色六角星作为插入)

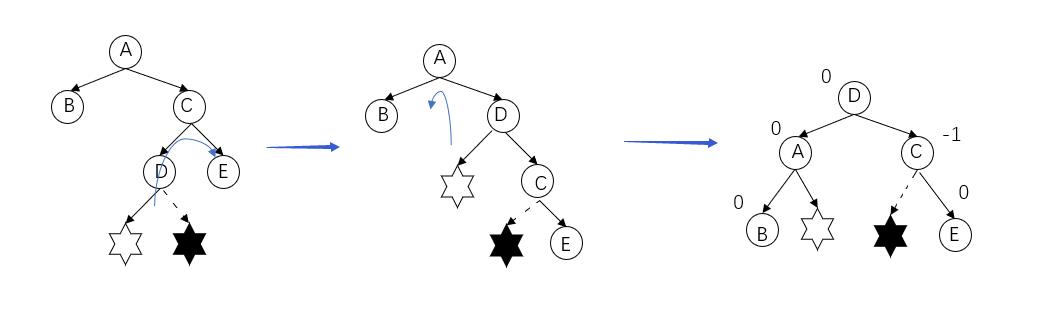
代码实现调整RL型就很简单了，先左旋，再右旋

void RightleftCir(Bactree **tree){//RL旋转
	SigelleftCir(&((*tree)->right));
	SigelrightCir(tree);
}

代码实现插入

#include<stdio.h>
#include<stdlib.h>
#include<Windows.h>
#pragma warning(disable:4996)

typedef int Elementtype;
typedef struct Balacetree{//二叉树信息
	Elementtype val;
	int hight;
	struct Balacetree *left;
	struct Balacetree *right;

}Bactree;


Bactree *TreeNodeCreate(Elementtype x){//创建树节点
	Bactree *tree = (Bactree *)malloc(sizeof(Bactree));
	tree->val = x;
	tree->hight = 1;
	tree->left = NULL;
	tree->right = NULL;
	return tree;
}

int GetHight(Bactree *tree){//求树高度
	if (!tree){
		return 0;
	}
	int H;
	int LH;
	int RH;
	LH = GetHight(tree->left);
	RH = GetHight(tree->right);
	H = LH > RH ? LH : RH;
	return H + 1;
}
void SigelleftCir(Bactree **tree){//LL旋转
	Bactree *temp = NULL;
	temp = (*tree)->left;
	(*tree)->left = temp->right;
	temp->right = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//调整后要保持每个结点高度正确。
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp; //要赋值给(*tree),不然temp才是正确的数

}
void SigelrightCir(Bactree **tree){//RR旋转，与LL一样
	Bactree *temp = NULL;
	temp = (*tree)->right;
	(*tree)->right = temp->left;
	temp->left = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp;

}

void LeftrightCir(Bactree **tree){//LR旋转
	SigelrightCir(&((*tree)->left));
	SigelleftCir(tree);
}
void RightleftCir(Bactree **tree){//RL旋转
	SigelleftCir(&((*tree)->right));
	SigelrightCir(tree);
}

Bactree *BalaceTreePush(Bactree **tree, Elementtype x){
	if (!(*tree)){     //插入结点
		*tree=TreeNodeCreate(x);
		return *tree;
	}
	if ((*tree)->val > x){  //x小的插入左边
		(*tree)->left = BalaceTreePush(&((*tree)->left), x);//往右边找，将结点返回给左指针
		//为什么放循环里，放循环里确认了一个方向，是左边
		if (GetHight((*tree)->left) - GetHight((*tree)->right) >= 2){//平衡因子
			if ((*tree)->left->val > x){//确认了第二个方向 左边
				SigelleftCir(tree);//LL
			}
			else{//右边
				LeftrightCir(tree);//LR
			}
		}
	}
	else{
		(*tree)->right = BalaceTreePush(&((*tree)->right), x);
		if (GetHight((*tree)->left) - GetHight((*tree)->right) <= -2){//注意是-2
			if ((*tree)->right->val < x){
				SigelrightCir(tree);
			}
			else{
				RightleftCir(tree);
			}
		}
	}
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//更新高度
	return *tree;

}

void Print(Bactree *tree){
	if (tree){
		Print(tree->left);
		printf("%d ", tree->val);
		Print(tree->right);
	}
}


int main(){
	Bactree *T = NULL;
	BalaceTreePush(&T, -10);
	BalaceTreePush(&T, -3);
	BalaceTreePush(&T, 0);
	BalaceTreePush(&T, 5);
	BalaceTreePush(&T, 9);
	BalaceTreePush(&T, 10);
	Print(T);

	system("pause");
	return 0;
}