小白都会的一道题！但是你能写几种？ 《建议收藏 慢慢品！》

Posted 2021-06-28 @了凡

前言

壁纸推荐

如有涉权，请联系我立删

博主简介

博主介绍：

– 本人是了凡，意义是希望本人任何时候以善良为先，以人品为重，喜欢了凡四训中的立命之学、改过之法、积善之方、谦德之效四训，更喜欢每日在简书上投稿日更的读书感悟笔名：三月_刘超。专注于 Go Web 后端，辅学Python、Java、算法、前端等领域。未来大家一起加油啊~

---

文章目录

• 前言
• • 壁纸推荐
  • 博主简介
• 题目
• 示例
• 题解1
• • 思路：
  • 题解
• 题解2
• • 思路：
  • 题解
• 题解3
• • 思路：
  • 题解
• 题解4
• • 思路：
  • 题解
• 题解5
• • 思路：
  • 题解
• 题解6
• • 思路：
  • 题解
• 题解7
• • 思路：
  • 题解
• 题解8
• • 思路：
  • 题解
• 题解9
• • 思路：
  • 题解

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

---

示例

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
①： 1 阶 + 1 阶
②： 2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
①： 1 阶 + 1 阶 + 1 阶
②： 1 阶 + 2 阶
③： 2 阶 + 1 阶

---

题解1

思路：

暴力
递归树

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}
public static int climbStairs(int n) {
    return climb_Stairs(0, n);
}
public static int climb_Stairs(int i, int n) {
      if (i > n) {
          return 0;
      }
      if (i == n) {
          return 1;
      }
      return climb_Stairs(i + 1, n) + climb_Stairs(i + 2, n);
}

---

题解2

思路：

数学：斐波那契数列公式
采用公式：

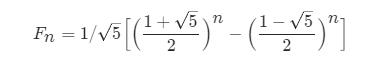
时间复杂度：O(logn)O(logn)

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

public static int climbStairs(int n) {
   double sqrt_5 = Math.sqrt(5);
    double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);
    return (int)(fib_n / sqrt_5);
}

---

题解3

思路：

斐波那契数

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

public int climbStairs(int n) {
    if (n == 1) {
        return 1;
    }
    int first = 1;
    int second = 2;
    for (int i = 3; i <= n; i++) {
        int third = first + second;
        first = second;
        second = third;
    }
    return second;
}

---

题解4

思路：

记忆话递归

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

 public int climbStairs(int n) {
    int memo[] = new int[n + 1];
    return climb_Stairs(0, n, memo);
}
public int climb_Stairs(int i, int n, int memo[]) {
   if (i > n) {
        return 0;
    }
    if (i == n) {
        return 1;
    }
    if (memo[i] > 0) {
        return memo[i];
    }
    memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);
    return memo[i];
}

---

题解5

思路：

动态规划
常规解法可以分成多个子问题，爬第n阶楼梯的方法数量，等于 2 部分之和

1. 爬上 n-1n−1 阶楼梯的方法数量。因为再爬1阶就能到第n阶
2. 爬上 n-2n−2 阶楼梯的方法数量，因为再爬2阶就能到第n阶
   

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

public int climbStairs(int n) {
    if (n == 1) {
        return 1;
    }
    int[] dp = new int[n + 1];
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

---

题解6

思路：

Binets 方法

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

public int climbStairs(int n) {
   int[][] q = {{1, 1}, {1, 0}};
    int[][] res = pow(q, n);
    return res[0][0];
}
public int[][] pow(int[][] a, int n) {
    int[][] ret = {{1, 0}, {0, 1}};
    while (n > 0) {
        if ((n & 1) == 1) {
            ret = multiply(ret, a);
        }
        n >>= 1;
        a = multiply(a, a);
    }
    return ret;
}
public int[][] multiply(int[][] a, int[][] b) {
    int[][] c = new int[2][2];
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
        }
    }
    return c;
}

---

题解7

思路：

两个变量方法：
这个方法较为取巧，就不用讲了吧

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

public static int climbStairs(int n) {
   	int a = 1;
   	int b = 2;
   	for (int i = 1; i < (n + 1) / 2; i++) {
		a = a + b;
		b = a + b;
	}
   	if (n % 2 == 0) {
   		return b;
   	}else {
   		return a;
   	}
}

---

题解8

思路：

通项公式：
f(n)f(n) 是齐次线性递推，根据递推方程 f(n) = f(n - 1) + f(n - 2)f(n)=f(n−1)+f(n−2)，我们可以写出这样的特征方程：

通过这个公式直接求第 n 项

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}
	
public int climbStairs(int n) {
    double sqrt5 = Math.sqrt(5);
    double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
    return (int) Math.round(fibn / sqrt5);
}

题解9

思路：

解法：map+递归，每个n只递归一次。

题解

public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	int rodeom = sc.nextInt();
	System.out.println(climbStairs(rodeom));
}

static Map map = new HashMap<>();
public int climbStairs(int n) {
    if(n<3)
        return n;
    else {
        int x,y;
        if((map.get(n-1) != null) &&(map.get(n-2) != null)){
            x = (int) map.get(n-1);
            y= (int) map.get(n-2);
        }else {
            x = climbStairs(n-1);
            y = climbStairs(n-2);
            map.put(n-1,x);
            map.put(n-2,y);
        }
        return x+y;
    }
}

---

后序每周持续更新！以上题解有个人书写和采集各方大佬，如有更多解法留言哦~

---