万万想不到 10行代码搞定一个决策树

Posted 2021-06-28 Real&Love

01决策树模拟实验

文章目录

• 01决策树模拟实验
• • 要求
  • 决策树简单介绍
  • 产生数据集
  • 划分训练集和测试集
  • 生成决策树
  • Cross-Validation法
  • 可视化决策树
  • 10行代码搞定决策树

要求

这是一个简单的实验，要求也特别简单

• 产生数据集：使用某种随机生成器产生10万个101维向量(每个分量非0即1)；其中每个向量的1-100维是条件属性，第101维是决策属性。

• 将数据集按照8:2随机划分为训练集(80%)和测试集(20%)

请使用sklearn或weka

• 分别以决策树深度为1、2、3、…、15完成训练集合上的建树过程，并记录相应的训练精度与测试精度

• 探究决策树规模与测试精度之间的关系，图示给出

• 通过此0-1决策树模拟实验以及相应的结果分析，你对决策树模型处理符号值数据分类预测有什么理解？

决策树简单介绍

这里只对决策树的一些概念进行一个简单的介绍，详细的介绍会在之后的博文探究

决策树是一种机器学习的方法。决策树的生成算法有ID3, C4.5和C5.0等。决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

决策树是一种十分常用的分类方法，需要监管学习（有教师的Supervised Learning），监管学习就是给出一堆样本，每个样本都有一组属性和一个分类结果，也就是分类结果已知，那么通过学习这些样本得到一个决策树，这个决策树能够对新的数据给出正确的分类。这里通过一个简单的例子来说明决策树的构成思路：

给出如下的一组数据，一共有十个样本（学生数量），每个样本有分数，出勤率，回答问题次数，作业提交率四个属性，最后判断这些学生是否是好学生。最后一列给出了人工分类结果。

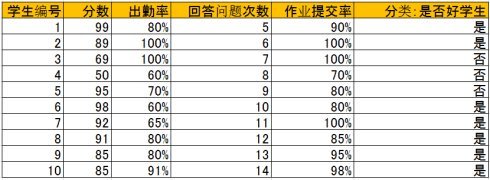
然后用这一组附带分类结果的样本可以训练出多种多样的决策树，这里为了简化过程，我们假设决策树为二叉树，且类似于下图：

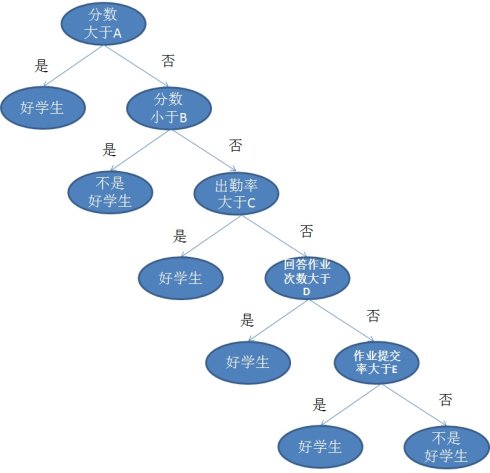
所以决策树的生成主要分以下两步，这两步通常通过学习已经知道分类结果的样本来实现。

1. 节点的分裂：一般当一个节点所代表的属性无法给出判断时，则选择将这一节点分成2个子节点（如不是二叉树的情况会分成n个子节点）

2. 阈值的确定：选择适当的阈值使得分类错误率最小 （Training Error）。

比较常用的决策树有ID3，C4.5和CART（Classification And Regression Tree），CART的分类效果一般优于其他决策树。下面介绍具体步骤。

ID3: 由增熵（Entropy）原理来决定那个做父节点，那个节点需要分裂。对于一组数据，熵越小说明分类结果越好。熵定义如下：
$$Entropy＝-sum[p(x_i)\ast \ast log\ast 2(P(x_i)]$$
其中$p(x_i)$ 为$x_i$出现的概率。假如是2分类问题，当A类和B类各占50%的时候，
$$Entropy=-（0.5\ast lo{g}_2(0.5)+0.5\ast lo{g}_2(0.5))=1$$
当只有A类，或只有B类的时候，
$$Entropy=-（1\ast lo{g}_2(1）+0）=0$$
所以当Entropy最大为1的时候，是分类效果最差的状态，当它最小为0的时候，是完全分类的状态。因为熵等于零是理想状态，一般实际情况下，熵介于0和1之间。

熵的不断最小化，实际上就是提高分类正确率的过程。

比如上表中的4个属性：单一地通过以下语句分类：

1. 分数小于70为【不是好学生】：分错1个

2. 出勤率大于70为【好学生】：分错3个

3. 问题回答次数大于9为【好学生】：分错2个

4. 作业提交率大于80%为【好学生】：分错2个

最后发现 分数小于70为【不是好学生】这条分错最少，也就是熵最小，所以应该选择这条为父节点进行树的生成，当然分数也可以选择大于71，大于72等等，出勤率也可以选择小于60，65等等，总之会有很多类似上述1~4的条件，最后选择分类错最少即熵最小的那个条件。而当分裂父节点时道理也一样，分裂有很多选择，针对每一个选择，与分裂前的分类错误率比较，留下那个提高最大的选择，即熵减最大的选择。

C4.5：通过对ID3的学习，可以知道ID3存在一个问题，那就是越细小的分割分类错误率越小，所以ID3会越分越细，比如以第一个属性为例：设阈值小于70可将样本分为2组，但是分错了1个。如果设阈值小于70，再加上阈值等于95，那么分错率降到了0，但是这种分割显然只对训练数据有用，对于新的数据没有意义，这就是所说的过度学习（Overfitting）。

分割太细了，训练数据的分类可以达到0错误率，但是因为新的数据和训练数据不同，所以面对新的数据分错率反倒上升了。决策树是通过分析训练数据，得到数据的统计信息，而不是专为训练数据量身定做。

就比如给男人做衣服，叫来10个人做参考，做出一件10个人都能穿的衣服，然后叫来另外5个和前面10个人身高差不多的，这件衣服也能穿。但是当你为10个人每人做一件正好合身的衣服，那么这10件衣服除了那个量身定做的人，别人都穿不了。

所以为了避免分割太细，c4.5对ID3进行了改进，C4.5中，优化项要除以分割太细的代价，这个比值叫做信息增益率，显然分割太细分母增加，信息增益率会降低。除此之外，其他的原理和ID3相同。

CART：分类回归树

CART是一个二叉树，也是回归树，同时也是分类树，CART的构成简单明了。

CART只能将一个父节点分为2个子节点。CART用GINI指数来决定如何分裂：

GINI指数：总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）。

a. 比如出勤率大于70%这个条件将训练数据分成两组：大于70%里面有两类：【好学生】和【不是好学生】，而小于等于70%里也有两类：【好学生】和【不是好学生】。

b. 如果用分数小于70分来分：则小于70分只有【不是好学生】一类，而大于等于70分有【好学生】和【不是好学生】两类。

比较a和b，发现b的凌乱程度比a要小，即GINI指数b比a小，所以选择b的方案。以此为例，将所有条件列出来，选择GINI指数最小的方案，这个和熵的概念很类似。

CART还是一个回归树，回归解析用来决定分布是否终止。理想地说每一个叶节点里都只有一个类别时分类应该停止，但是很多数据并不容易完全划分，或者完全划分需要很多次分裂，必然造成很长的运行时间，所以CART可以对每个叶节点里的数据分析其均值方差，当方差小于一定值可以终止分裂，以换取计算成本的降低。

CART和ID3一样，存在偏向细小分割，即过度学习（过度拟合的问题），为了解决这一问题，对特别长的树进行剪枝处理，直接剪掉。

产生数据集

这里我们会用sklearn来进行实验，通过查阅了sklearn中文文档，利用内置的样本的随机生成器生成我们需要的101维的数据

我这里不对生成器做详细解释，具体介绍可以查阅文档，我用的生成器是多标签的生成器

make_multilabel_classification 生成多个标签的随机样本，反映从a mixture of topics（一个混合的主题）中引用a bag of words （一个词袋）。每个文档的主题数是基于泊松分布随机提取的，同时主题本身也是从固定的随机分布中提取的。同样地，单词的数目是基于泊松分布提取的，单词通过多项式被抽取，其中每个主题定义了单词的概率分布。在以下方面真正简化了 bag-of-words mixtures （单词混合包）：

• 独立绘制的每个主题词分布，在现实中，所有这些都会受到稀疏基分布的影响，并将相互关联。
• 对于从文档中生成多个主题，所有主题在生成单词包时都是同等权重的。
• 随机产生没有标签的文件，而不是基于分布（base distribution）来产生文档
• 

首先定义我们的参数

n_samples = 100000 # 100000个数据
n_features = 100 # 100个特征
n_classes = 1 # 分两类 [0 1]两类
MAX_depth = 15 # 递归树最大的深度

接着就开始生成我们的101维的数据

# 生成数据
X,y = make_multilabel_classification(n_samples=n_samples,n_features=n_features,n_classes=n_classes)
X = X%2 # 得到的特征值为0或1
print('X = ', X, X.shape)
print('y = ', y, y.shape)

X =  [[0. 0. 0. ... 0. 0. 0.]
 [1. 0. 0. ... 0. 0. 1.]
 [1. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 1. 0. ... 0. 1. 0.]
 [0. 0. 0. ... 0. 0. 0.]] (100000, 100)
y =  [[0]
 [0]
 [0]
 ...
 [1]
 [0]
 [1]] (100000, 1)

我们可以看到我们的结果，我们生成了10万个100维的数据，作为我们的X，如何对应的还有10万个1维的数据，对应着我们的y，一个是我们的输入，另一个是我们的输出

划分训练集和测试集

我们将数据集按照8:2随机划分为训练集(80%)和测试集(20%)，所以我们设置的test_size = 0.2就是百分之20会作为我们的测试集

# 将原始数据按照比例分割为“测试集”和“训练集，test_size = 0.2就是20%为测试集
X_train,X_test, y_train, y_test =train_test_split(X,y,test_size=0.2,random_state=22)

生成决策树

分别以决策树深度为1、2、3、…、15完成训练集合上的建树过程

我们在前面设置我们的最大深度为15，所以我们这里进行一个迭代的建树过程

for i in range(1,MAX_depth+1):
    max_depth = i
    clf = tree.DecisionTreeClassifier(max_depth=max_depth)
    clf = clf.fit(X_train,y_train)
    test_score = clf.score(X_test,y_test)
    train_socre = clf.score(X_train,y_train)
    print('决策树深度 max depth = {:2}\\t\\t测试准确率 = {:.2f}%\\t\\t\\t 训练准确率 = {:.2f}%'
          .format(i,test_score*100,train_socre*100))

决策树深度 max depth =  1		测试准确率 = 77.05%			 训练准确率 = 77.45%
决策树深度 max depth =  2		测试准确率 = 83.58%			 训练准确率 = 83.67%
决策树深度 max depth =  3		测试准确率 = 87.63%			 训练准确率 = 87.49%
决策树深度 max depth =  4		测试准确率 = 88.91%			 训练准确率 = 89.20%
决策树深度 max depth =  5		测试准确率 = 89.33%			 训练准确率 = 89.85%
决策树深度 max depth =  6		测试准确率 = 89.69%			 训练准确率 = 89.88%
决策树深度 max depth =  7		测试准确率 = 91.02%			 训练准确率 = 91.26%
决策树深度 max depth =  8		测试准确率 = 92.08%			 训练准确率 = 92.50%
决策树深度 max depth =  9		测试准确率 = 92.95%			 训练准确率 = 93.55%
决策树深度 max depth = 10		测试准确率 = 93.27%			 训练准确率 = 93.92%
决策树深度 max depth = 11		测试准确率 = 93.49%			 训练准确率 = 94.16%
决策树深度 max depth = 12		测试准确率 = 93.44%			 训练准确率 = 94.67%
决策树深度 max depth = 13		测试准确率 = 92.99%			 训练准确率 = 95.26%
决策树深度 max depth = 14		测试准确率 = 92.88%			 训练准确率 = 95.97%
决策树深度 max depth = 15		测试准确率 = 92.99%			 训练准确率 = 96.62%

我们可以得到我们的结果，仔细分析一下结果，随着我们的决策树深度的增加，我们的训练精度不断的上升，但是我们的测试精度似乎在达到某一深度以后，测试精度就会下降，这里我们可视化了一下

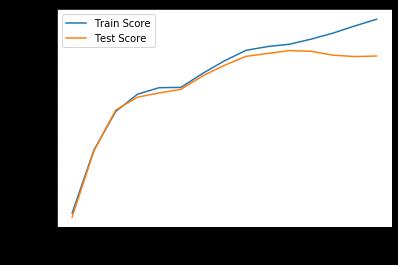
可能还是不够明显，那我就加深我们的深度，我直接加深到深度为100，我们看一下结果

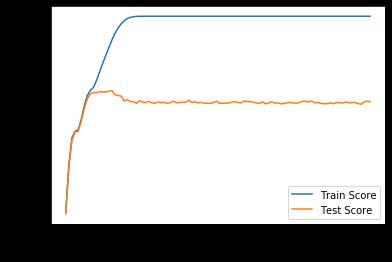
我们可以看到结果，我们的深度加深到一定程度后，测试精度达到最大值，但是随着深度的增加，我们的训练精度会逐渐变小，然后收敛在到某一值，训练精度会不断加深，最后变为100%

出现这样的原因就是过拟合，出现了过拟合的问题，导致我们的训练精度最后能够很大很大，但是这个模型的泛化性就不够了，对其他的数据，或者说其他生成的数据，准确率就不够高。所以在我们决策树分类问题中，应该选择一个比较好的深度，这样有助于我们得到一个更加好的模型，而不是过拟合或者欠拟合

from sklearn.metrics import classification_report
print(classification_report(y_train,predicted))

              precision    recall  f1-score   support

           0       0.98      0.92      0.95     26367
           1       0.96      0.99      0.98     53633

    accuracy                           0.97     80000
   macro avg       0.97      0.95      0.96     80000
weighted avg       0.97      0.97      0.97     80000

Cross-Validation法

决策树训练的时候，一般会采取Cross-Validation法：比如一共有10组数据：

第一次. 1到9做训练数据， 10做测试数据

第二次. 2到10做训练数据，1做测试数据

第三次. 1，3到10做训练数据，2做测试数据，以此类推

做10次，然后大平均错误率。这样称为 10 folds Cross-Validation。

比如 3 folds Cross-Validation 指的是数据分3份，2份做训练，1份做测试。

这里是用深度为15的模型进行Cross-Validation，参数cv=10，相当于会分10份

from sklearn.model_selection import cross_val_score
acc = cross_val_score(clf,X_train,y_train,cv=10)
acc

array([0.928625, 0.93225 , 0.92825 , 0.928625, 0.928375, 0.930625,
       0.927375, 0.924375, 0.927625, 0.93475 ])

可视化决策树

data = tree.export_graphviz(clf, out_file='tree.dot')
# graph = graphviz.Source(data)
tree.plot_tree(clf)

export_graphviz 还支持各种美化，包括通过他们的类着色节点（或回归值），如果需要，还能使用显式变量和类名。Jupyter notebook也可以自动内联式渲染这些绘制节点:

import pydotplus
with open('tree.dot', 'w') as f:
    dot_data = tree.export_graphviz(clf, out_file=None)
    f.write(dot_data)
 
# 生成pdf文件
dot_data = tree.export_graphviz(clf, out_file=None,feature_names=feature_names,class_names=class_names,  
                                filled=True, rounded=True, special_characters=True) 
graph = pydotplus.graph_from_dot_data(dot_data)
 
## 保存图像到pdf文件
graph.write_pdf("tree.pdf")

我们还可以保存成其他文件

graph.write_png('tree.png') # png文件
graph.write_fig('tree.fig') # fig文件
graph.write_jpeg('tree.jpeg') # jpeg文件
graph.write_jpg('tree.jpg') # jpg文件

不过如果是10万数据集的决策树，太大了，图片太模糊了，这里我们可视化一下100规模的数据集的生成的决策树

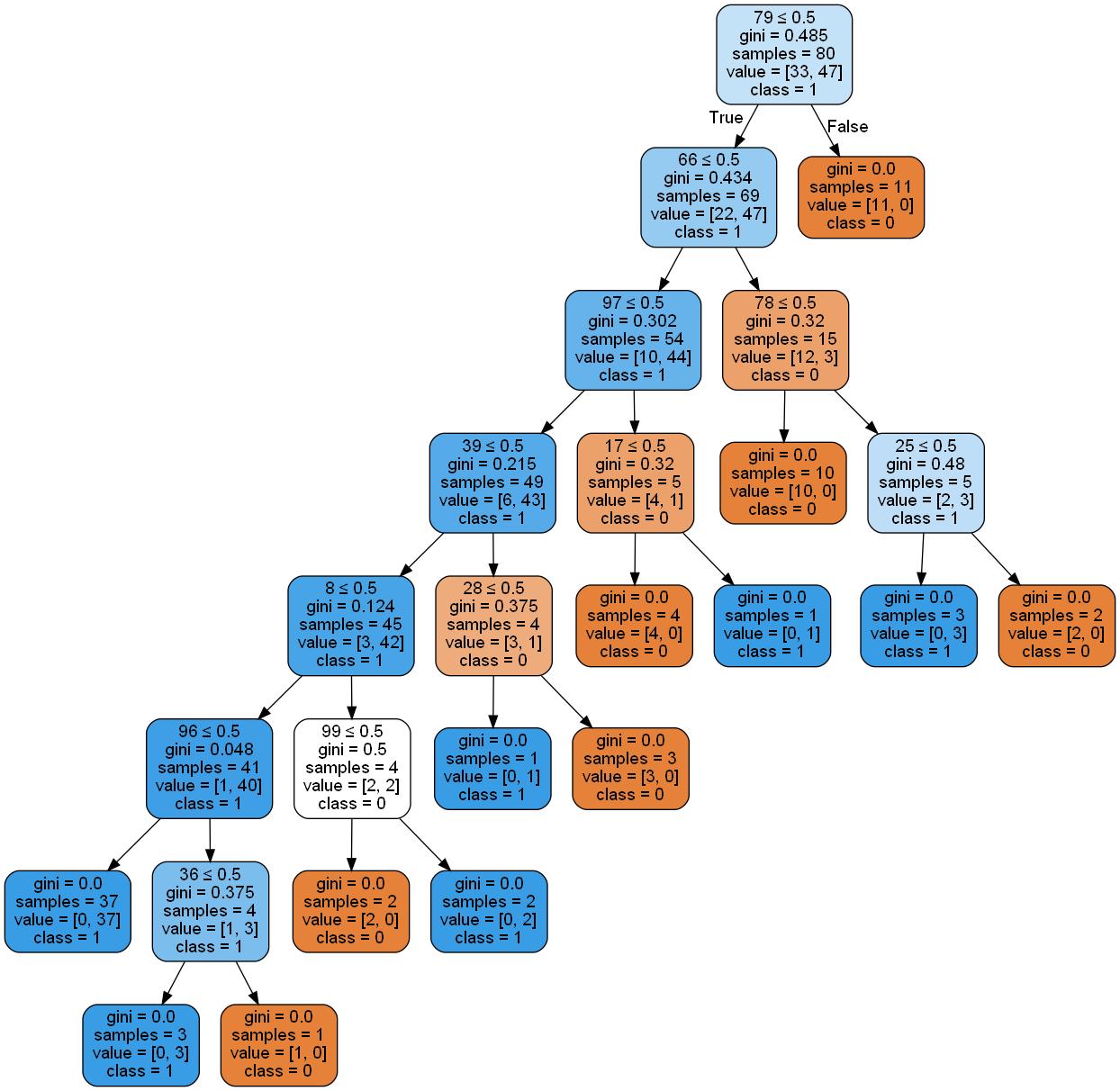
10行代码搞定决策树

这里不包括导入库

X,y = make_multilabel_classification(n_samples=n_samples,n_features=n_features,n_classes=n_classes)
X = X%2 # 得到的特征值为0或1
X_train,X_test, y_train, y_test =train_test_split(X,y,test_size=0.2,random_state=22)
for i in range(1,15+1):
    max_depth = i
    clf = tree.DecisionTreeClassifier(max_depth=max_depth)
    clf = clf.fit(X_train,y_train)
    test_score = clf.score(X_test,y_test)
    train_socre = clf.score(X_train,y_train)
    print('决策树深度 max depth = {:2}\\t\\t测试准确率 = {:.2f}%\\t\\t\\t 训练准确率 = {:.2f}%'.format(i,test_score*100,train_socre*100))