运筹系列74：MIP的启发式方法

Posted 2021-06-28 IE06

首先定义MIP问题如下：

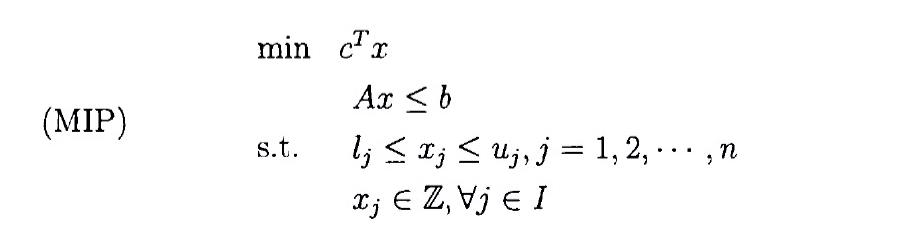
1. 圆整启发式算法

圆整启发式算法可以看做是广度优先的搜索方法，尽量一次把变量都变为整数，有两个事情要做：选择圆整变量、选择上圆整还是下圆整。

1.1 简单圆整

若$A_{.j}\ge 0$，称变量$x_j$平凡向下可圆整（即向下取整仍保持约束可行）；反之叫平凡向上可圆整。为方便描述，定义$A_{.j}$中负系数的个数称为下锁数，正系数的个数称为上锁数，两者的最小值称为变量$x_j$的锁数。
依次搜索变量，遇到平凡向下可圆整，则向下进行圆整；遇到平凡向上可圆整，则向上进行圆整，如果运气好的话把所有非整数变量都变成整数了，则得到一个可行解。

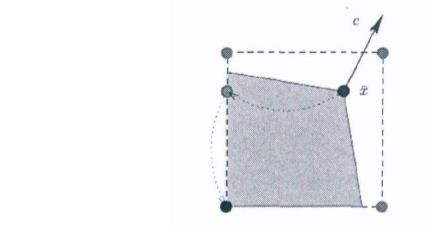
注意，简单圆整在可行域内移动，不一定能达到分枝树的顶点。

1.2 圆整

依次对变量进行圆整：

1. 若当前所有约束都ok，则接下来选择锁数最大的变量进行圆整。若有多个变量的最大锁数相同，则选择目标函数增量最小的变量进行圆整（这里开始突破简单圆整的限制，约束可能变为不可行）
2. 若会使约束$i$变得不可行，则下一个变量$j$对应的$a_{ij}>0$的话，则向下圆整，否则向上圆整，同样选择锁数最大的变量进行圆整。
3. 如果不可行约束数目没有减少，则圆整停止。

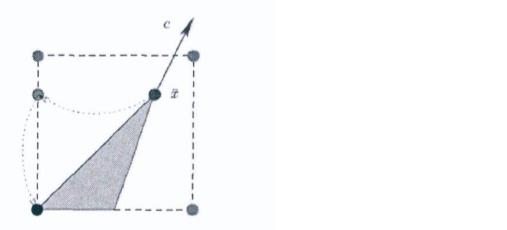
同样，圆整方法也不一定能达到分枝树的顶点。在突破约束限制后如果回不来，则算法停止。

1.3 shifting

移位算法尝试挪动已经变成整数的变量，探索新的天地。如下图，第一步变量变为整数后，第二条约束不满足了，此时对变量进行移位，挪到了可行域之内。也就是说，在仅仅改变分数变量回不来时，尝试去改变整数变量。

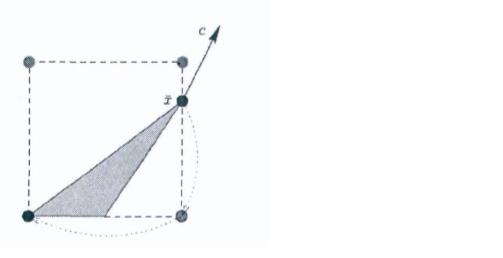
1. 存在不可行约束时，选择违反度最小的约束，若有分数变量，则选择锁数最小的分数变量进行圆整。
2. 若所有不可行约束都不包含分数变量，则考虑进行整数移位，选择迭代数最小的整数进行挪移。
3. 若没有不可行约束，恢复圆整启发式算法

2. 潜水启发式算法

diving heuristic的思路是用圆整方法快速进行BB树的深度探索（用对偶单纯形法），尽快到达可行解叶子节点，可以看做是一个深度优先的算法，终止条件如下：
1）LP不可行
2）LP目标值比已有的目标值更差
3）超出迭代限制（比如迭代次数要求，一般要求迭代次数小于当前节点LP迭代次数的5%）
如何选择分支变量和分支方向，是启发式算法的主要内容。
优先应该选择0-1变量进行圆整，因为一旦圆整就相当于固定。

2.1 fractionality diving

分数潜水，选择分数部分最小的变量进行圆整。

2.2 coefficient diving

系数潜水，亦称锁数潜水，选择锁数最小的变量进行圆整，其目的是为了减少对约束条件可行性的影响。

2.3 line search diving

用一条线段连接LP根节点和当前解，并向两端延长直到和第一个整数约束超平面相交，变量选择距离比例最小的：

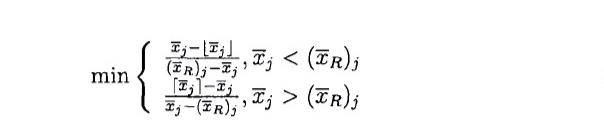
其中$x$是当前解，$x_R$是根节点解

2.4 guided diving

导向潜水，和分数潜水很像，只不过是和MIP可行解计算差值，选择差值最小的变量和对应的方向进行圆整。

2.5 Pseudocost diving

首先计算$x_j$圆整后目标函数的单位变化量，然后计算左、右分支所有子问题的平均单位变化量，取小的那个方向进行圆整。至于具体取哪个变量进行圆整，按照如下规则，此规则结合了分数和伪费用：

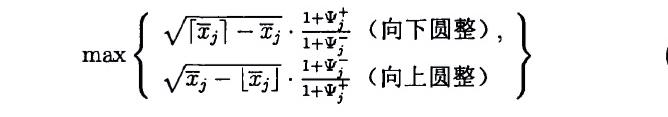
2.6 vector length diving

主要用于处理set covering问题，思路是选择一个在约束中出现次数最多，且对目标值退化影响最小的变量。
圆整方向沿着与目标函数相反的方向，根据下述规则选择变量：

其中$f$是分数变量，A是所在列非零元素的个数。

3. Octane算法

Octane算法适用于纯0-1规划问题，全称为OCT Ahedral Neighborhood Search，其思想来源于相交割平面方法，
定义 K : = { x ∣ − e / 2 ≤ x ≤ e / 2 } K:=\\{x|-e/2\\le x\\le e/2\\} K:={x∣−e/2≤x≤e/2}为单位超立方体， K ∗ : = { x ∣ ∣ ∣ x ∣ ∣ 1 ≤ n / 2 } K^*:=\\{x|||x||_1\\le n/2\\} K∗:={x∣∣∣x∣∣1​≤n/2}为外切八面体。
单位超立方体和外切八面体刚好一一对应，我们做个挪移，两者的关系为：
$e/2+\delta /2=x$，其中 δ ∈ { ± 1 } n \\delta\\in\\{\\pm 1\\}^n δ∈{±1}n