运筹系列68：Julia的图论包

Posted 2021-06-28 IE06

一些小技巧：

using ProgressMeter
@showprogress 1 "Retrieving Julian info..." for ...

using JSON
# write to file
userdata = Dict("nodes"=>usernodes, "links"=>userlinks)
open("Julians.json", "w") do f
  JSON.print(f, userdata, 2)
end

用D3进行可视化：

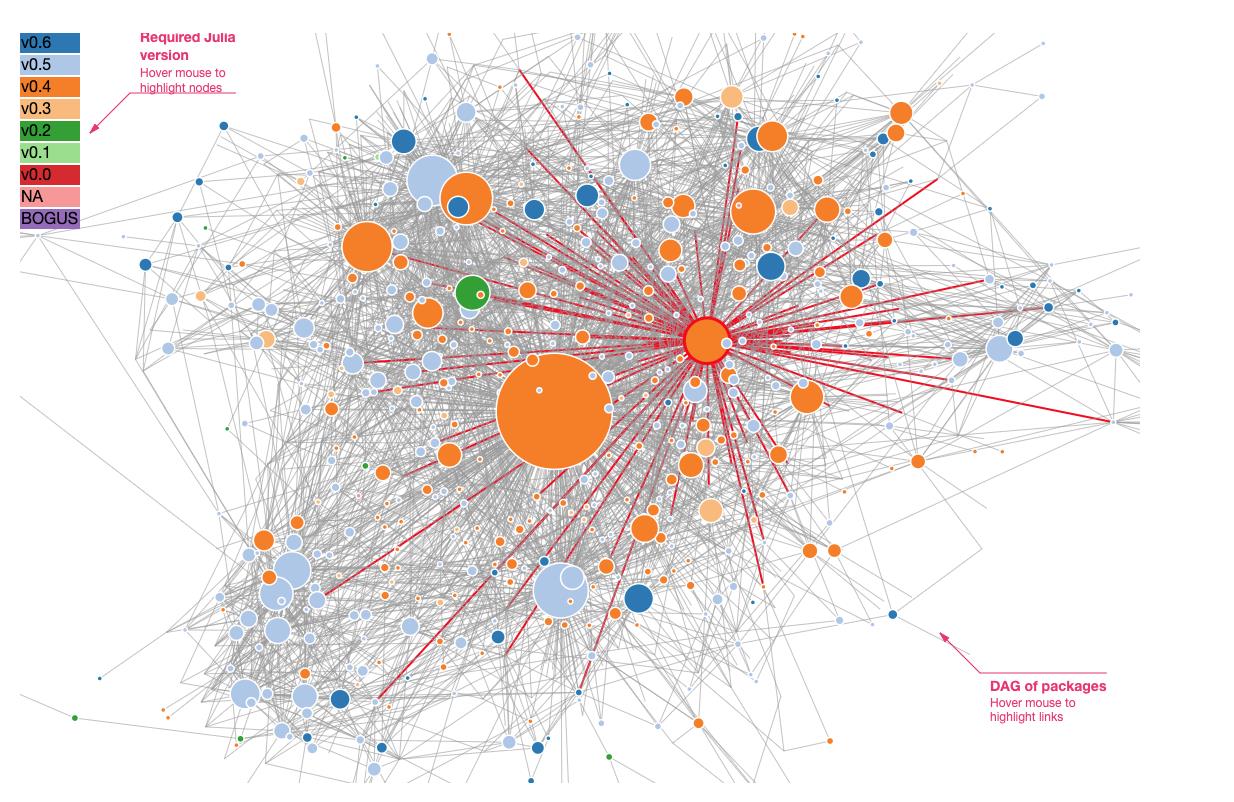
教程参见https://juliagraphs.org/LightGraphs.jl/latest/

1. 优越的性能

这篇文章测试了目前开源的六个图论框架，四个是Python&C++，一个是纯Python（基准），还有一个是Julia的LightGraph.jl，发现Julia的运算速度十分惊人（因为一开始本来没打算测Julia的）。并且与其他框架相比，Julia可以显式控制是否使用并行。

• 这6个框架是：
  graph-tool, v2.31 (Peixoto 2014)
  igraph, v0.8.2 (Csardi and Nepusz 2006)
  networkit, v6.1.0 (Staudt, Sazonovs, and Meyerhenke 2016)
  networkx, v2.4 (Hagberg, Swart, and S Chult 2008)
  SNAP, v5.0.0 (Leskovec and Sosič 2016)
  lightgraphs, v2.0-dev (Seth Bromberger and contributors 2017)

• 测试的5个问题如下：
  loading the data
  single source shortest path
  page rank
  k-core decomposition
  strongly connected components

• 测试数据集为：
  Amazon product co-purchasing network from March 2 2003, 262k nodes, 1.2m edges
  Web graph from Google, 875k nodes, 5.1m edges
  Pokec online social network, 1.6m nodes, 30.6m edges

• 结果：
  lightGraph除了loading比较慢之外，在算法上比其他包要快很多。
  

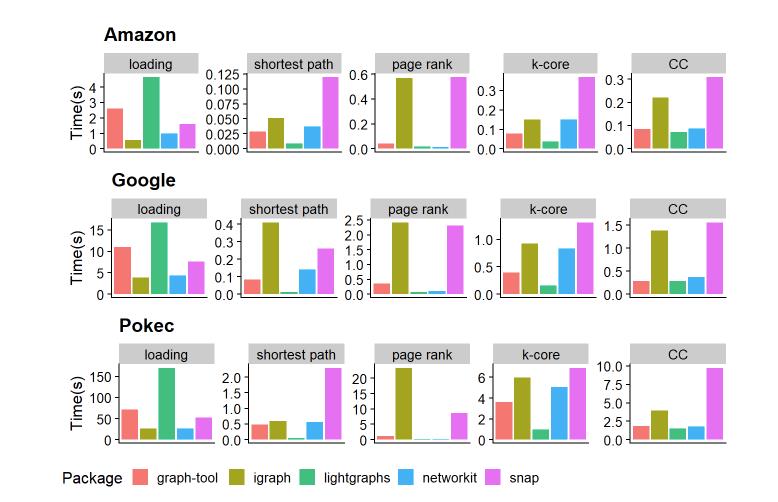
2. 基础

2.1 定义

sing LightGraphs
using Graphplot

G₁ = Graph(3) # graph with 3 vertices

# make a triangle
add_edge!(G₁, 1, 2)
add_edge!(G₁, 1, 3)
add_edge!(G₁, 2, 3)

gplot(G₁, nodelabel=1:3)

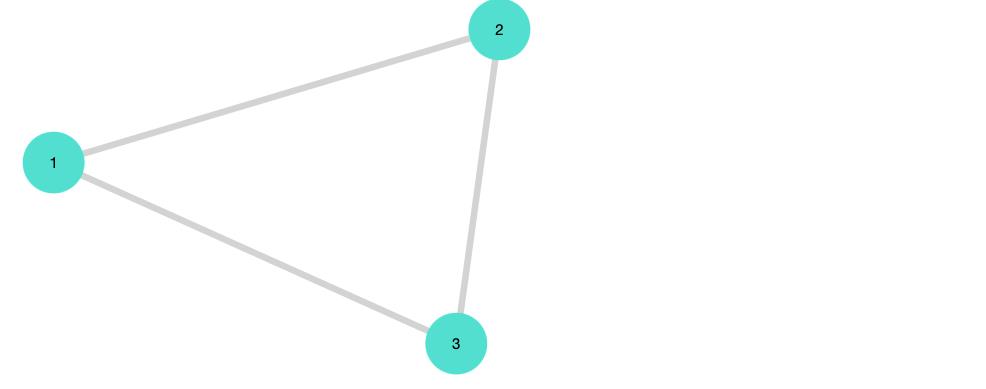
亦可以使用矩阵：

A = [0 1 1
    1 0 1
    1 1 0]

G₂ = Graph(A)

或者随机生成边：

G = Graph(3,3)
G = DiGraph(3,3)
gplot(G)

另外有一些预定义的图，叫generator：

for shape in ["bull","house"]
    G = smallgraph(shape)
    display(gplot(G))
end

G = CliqueGraph(3,4)
gplot(G)

另外可以用嵌套方式：

# metal plate
□ = Graph(4)
add_edge!(□, 1, 2)
add_edge!(□, 1, 3)
add_edge!(□, 2, 4)
add_edge!(□, 3, 4)

# airplane skeleton
skeleton = Graph(11)
add_edge!(skeleton, 1, 2)
add_edge!(skeleton, 2, 3)
add_edge!(skeleton, 3, 4)
add_edge!(skeleton, 4, 5)
add_edge!(skeleton, 3, 6)
add_edge!(skeleton, 3, 7)
add_edge!(skeleton, 3, 8)
add_edge!(skeleton, 3, 9)
add_edge!(skeleton, 9, 10)
add_edge!(skeleton, 9, 11)

gplot(cartesian_product(□, skeleton))

2.2 函数

G = smallgraph("house")
# 获取节点
nvertices = nv(G) # number of vertices
nedges = ne(G)    # number of edges
for v in vertices(G)
    println("vertex $v")
end
for e in edges(G)
    u, v = src(e), dst(e)
    println("edge $u - $v")
end
adjacency_matrix(G) # 邻接矩阵
incidence_matrix(G) # 关联矩阵
laplacian_matrix(G)  # 拉普拉斯矩阵
gplot(G, nodelabel=1:nvertices, edgelabel=1:nedges) # 绘图

# 增加/删除点和边
add_vertex!(G)
add_edge!(G, 5, 6)
gplot(G, nodelabel=1:nv(G), edgelabel=1:ne(G))
rem_vertex!(G, 1)
gplot(G, nodelabel=1:nv(G), edgelabel=1:ne(G))