LeetCode 877石子游戏[动态规划 数学] HERODING的LeetCode之路

Posted 2021-06-28 HERODING23

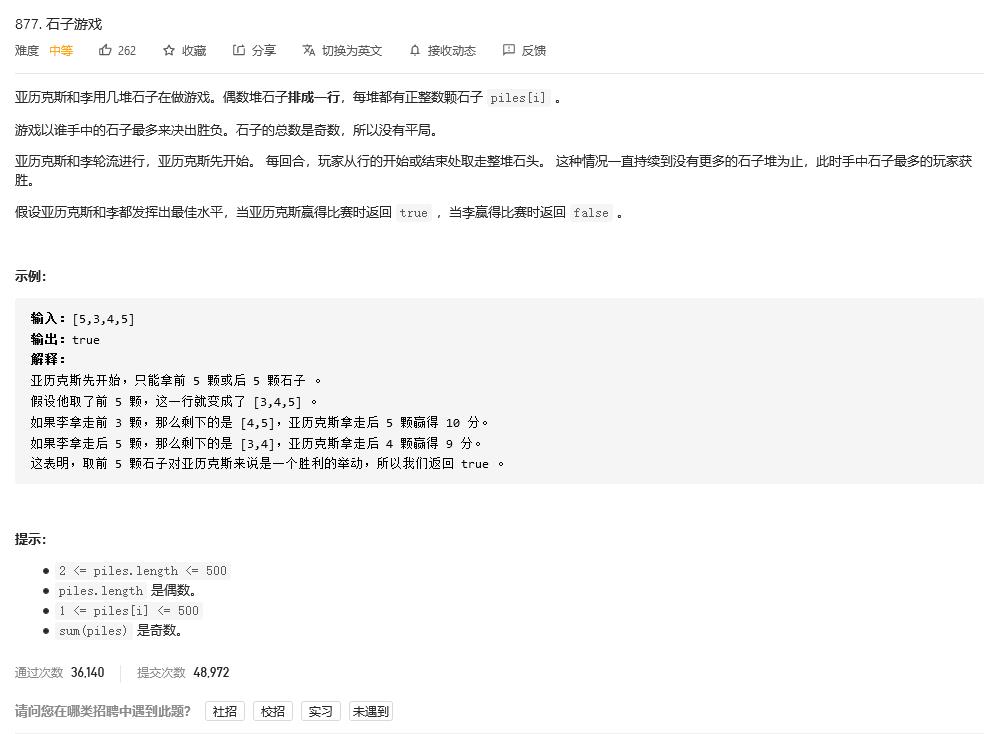解题思路：
既然是每次都是最优选择，那么递归所有选择找最优不免为一种方法，但是时间复杂度为（2^n），只好用动态规划来代替，dp[i][j]表示从i到j长度的石头堆二人选择的最大差值，只要dp[i][j] > 0，那么亚历克斯就赢，否则输，代码如下：

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int len = piles.size();
        vector<vector<int>> dp(len + 1, vector<int>(len + 1));
        for(int i = 1; i <= len; i ++) {
            dp[i][i] = piles[i - 1];
        }
        for(int i = len - 1; i > 0; i --) {
            for(int j = i + 1; j <= len; j ++) {
                dp[i][j] = max(piles[i - 1] - dp[i + 1][j], piles[j - 1] - dp[i][j - 1]);
            }
        }
        return dp[1][len];
    }
};

观察发现i只与i - 1有关，依然可以使用滚动数组进行优化，代码如下：

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int len = piles.size();
        vector<int> dp(len + 1);
        for(int i = 1; i <= len; i ++) {
            dp[i] = piles[i - 1];
        }
        for(int i = len - 1; i > 0; i --) {
            for(int j = i + 1; j <= len; j ++) {
                dp[j] = max(piles[i - 1] - dp[j], piles[j - 1] - dp[j - 1]);
            }
        }
        return dp[len];
    }
};

当然了，其实仔细思考你就能明白，只要是先手，每次挑选的都是最优的情况，又是发挥最好的情况，所以一定能赢得比赛（奇数颗石子），代码如下：

class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true;
    }
};