一文搞定搜索！

Posted 2021-06-28 Big sai

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了一文搞定搜索！相关的知识，希望对你有一定的参考价值。

大话搜索

搜索一般指在有限的状态空间中进行枚举，通过穷尽所有的可能来找到符合条件的解或者解的个数。根据搜索方式的不同，搜索算法可以分为 DFS，BFS，A*算法等。这里只介绍 DFS 和 BFS，以及发生在 DFS 上一种技巧-回溯。

搜索问题覆盖面非常广泛，并且在算法题中也占据了很高的比例。我甚至还在公开演讲中提到了 「前端算法面试中搜索类占据了很大的比重，尤其是国内公司」。

搜索专题中的子专题有很多，而大家所熟知的 BFS，DFS 只是其中特别基础的内容。除此之外，还有状态记录与维护，剪枝，联通分量，拓扑排序等等。这些内容，我会在这里一一给大家介绍。

另外即使仅仅考虑 DFS 和 BFS 两种基本算法，里面能玩的花样也非常多。比如 BFS 的双向搜索，比如 DFS 的前中后序，迭代加深等等。

关于搜索，其实在二叉树部分已经做了介绍了。而这里的搜索，其实就是进一步的泛化。数据结构不再局限于前面提到的数组，链表或者树。而扩展到了诸如二维数组，多叉树，图等。不过核心仍然是一样的，只不过数据结构发生了变化而已。

搜索的核心是什么？

实际上搜索题目「本质就是将题目中的状态映射为图中的点，将状态间的联系映射为图中的边。根据题目信息构建状态空间，然后对状态空间进行遍历，遍历过程需要记录和维护状态，并通过剪枝和数据结构等提高搜索效率。」

状态空间的数据结构不同会导致算法不同。比如对数组进行搜索，和对树，图进行搜索就不太一样。

再次强调一下，我这里讲的数组，树和图是「状态空间」的逻辑结构，而不是题目给的数据结构。比如题目给了一个数组，让你求数组的搜索子集。虽然题目给的线性的数据结构数组，然而实际上我们是对树这种非线性数据结构进行搜索。这是因为这道题对应的「状态空间是非线性的」。

对于搜索问题，我们核心关注的信息有哪些？又该如何计算呢？这也是搜索篇核心关注的。而市面上很多资料讲述的不是很详细。搜索的核心需要关注的指标有很多，比如树的深度，图的 DFS 序，图中两点间的距离等等。「这些指标都是完成高级算法必不可少的，而这些指标可以通过一些经典算法来实现」。这也是为什么我一直强调「一定要先学习好基础的数据结构与算法」的原因。

不过要讲这些讲述完整并非容易，以至于如果完整写完可能需要花很多的时间，因此一直没有动手去写。

另外由于其他数据结构都可以看做是图的特例。因此研究透图的基本思想，就很容易将其扩展到其他数据结构上，比如树。因此我打算围绕图进行讲解，并逐步具象化到其他特殊的数据结构，比如树。

状态空间

结论先行：「状态空间其实就是一个图结构，图中的节点表示状态，图中的边表示状态之前的联系，这种联系就是题目给出的各种关系」。

搜索题目的状态空间通常是非线性的。比如上面提到的例子：求一个数组的子集。这里的状态空间实际上就是数组的各种组合。

对于这道题来说，其状态空间的一种可行的划分方式为：

长度为 1 的子集
长度为 2 的子集
。。。
长度为 n 的子集（其中 n 为数组长度）

而如何确定上面所有的子集呢。

一种可行的方案是可以采取类似分治的方式逐一确定。

比如我们可以：

先确定某一种子集的第一个数是什么
再确定第二个数是什么
。。。

如何确定第一个数，第二个数。。。呢？

「暴力枚举所有可能就可以了。」

❝
这就是搜索问题的核心，其他都是辅助，所以这句话请务必记住。
❞

所谓的暴力枚举所有可能在这里就是尝试数组中所有可能的数字。

比如第一个数是什么？很明显可能是数组中任意一项。ok，我们就枚举 n 种情况。
第二个数呢？很明显可以是除了上面已经被选择的数之外的任意一个数。ok，我们就枚举 n - 1 种情况。

据此，你可以画出如下的决策树。

（下图描述的是对一个长度为 3 的数组进行决策的部分过程，树节点中的数字表示索引。即确定第一个数有三个选择，确定第二个数会根据上次的选择变为剩下的两个选择）

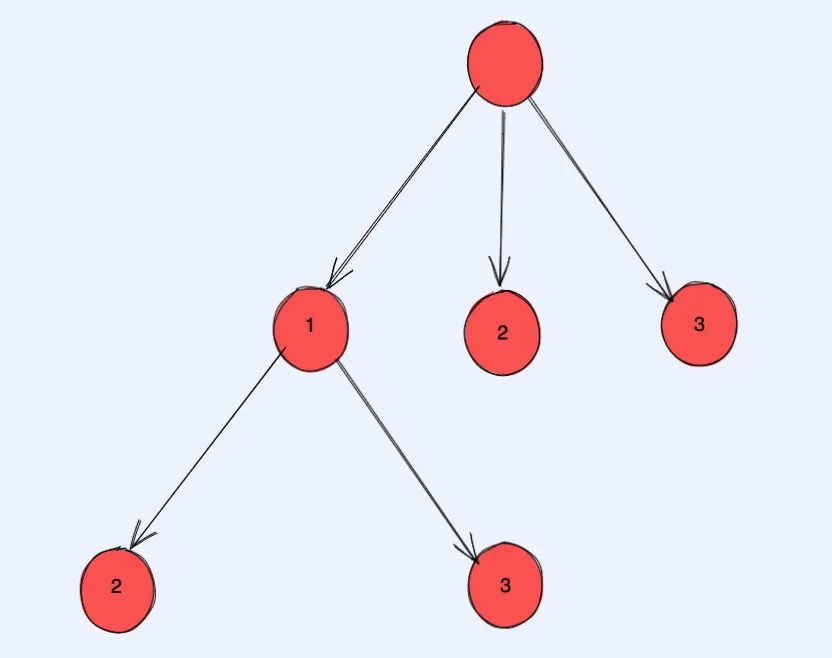
决策过程动图演示：

搜索-决策树

「一些搜索算法就是基于这个朴素的思想，本质就是模拟这个决策树」。这里面其实也有很多有趣的细节，后面我们会对其进行更加详细的讲解。而现在大家只需要对「解空间是什么以及如何对解空间进行遍历有一点概念就行了。」 后面我会继续对这个概念进行加深。

这里大家只要记住「状态空间就是图，构建状态空间就是构建图。如何构建呢？当然是根据题目描述了」 。

DFS 和 BFS

DFS 和 BFS 是搜索的核心，贯穿搜索篇的始终，因此有必要先对其进行讲解。

DFS

DFS 的概念来自于图论，但是搜索中 DFS 和图论中 DFS 还是有一些区别，搜索中 DFS 一般指的是通过递归函数实现暴力枚举。

❝
如果不使用递归，也可以使用栈来实现。不过本质上是类似的。
❞

首先将题目的「状态空间映射到一张图，状态就是图中的节点，状态之间的联系就是图中的边」，那么 DFS 就是在这种图上进行「深度优先」的遍历。而 BFS 也是类似，只不过遍历的策略变为了「广度优先」，一层层铺开而已。所以「BFS 和 DFS 只是遍历这个状态图的两种方式罢了，如何构建状态图才是关键」。

本质上，对上面的图进行遍历的话会生成一颗「搜索树」。为了「避免重复访问，我们需要记录已经访问过的节点」。这些是「所有的搜索算法共有的」，后面不再赘述。

如果你是在树上进行遍历，是不会有环的，也自然不需要为了「避免环的产生记录已经访问的节点」，这是因为树本质上是一个简单无环图。

算法流程

首先将根节点放入「stack」中。
从stack中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它某一个尚未检验过的直接子节点加入「stack」中。
重复步骤 2。
如果不存在未检测过的直接子节点。将上一级节点加入「stack」中。重复步骤 2。
重复步骤 4。
若「stack」为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。

❝
这里的 stack 可以理解为自实现的栈，也可以理解为调用栈
❞

算法模板

下面我们借助递归来完成 DFS。

const visited = {}
function dfs(i) {
 if (满足特定条件）{
  // 返回结果 or 退出搜索空间
 }

 visited[i] = true // 将当前状态标为已搜索
 for (根据i能到达的下个状态j) {
  if (!visited[j]) { // 如果状态j没有被搜索过
   dfs(j)
  }
 }
}

常用技巧

前序遍历与后序遍历

DFS 常见的形式有「前序和后序」。二者的使用场景也是截然不同的。

上面讲述了搜索本质就是在状态空间进行遍历，空间中的状态可以抽象为图中的点。那么如果搜索过程中，当前点的结果需要依赖其他节点（大多数情况都会有依赖），那么遍历顺序就变得重要。

比如当前节点需要依赖其子节点的计算信息，那么使用后序遍历自底向上递推就显得必要了。而如果当前节点需要依赖其父节点的信息，那么使用先序遍历进行自顶向下的递归就不难想到。

比如下文要讲的计算树的深度。由于树的深度的递归公式为：。其中 f(x) 表示节点 x 的深度，并且 x 是 y 的子节点。很明显这个递推公式的 base case 就是根节点深度为一，通过这个 base case 我们可以递推求出树中任意节点的深度。显然，使用先序遍历自顶向下的方式统计是简单而又直接的。

再比如下文要讲的计算树的子节点个数。由于树的子节点递归公式为：其中 x 为树中的某一个节点，为树中节点的子节点。而 base case 则是没有任何子节点(也就是叶子节点)，此时。因此我们可以利用后序遍历自底向上来完成子节点个数的统计。

关于从递推关系分析使用何种遍历方法，我在《91 天学算法》中的基础篇中的《模拟，枚举与递推》子专题中对此进行了详细的描述。91 学员可以直接进行查看。关于树的各种遍历方法，我在树专题中进行了详细的介绍。

迭代加深

迭代加深本质上是一种可行性的剪枝。关于剪枝，我会在后面的《回溯与剪枝》部分做更多的介绍。

所谓迭代加深指的是「在递归树比较深的时候，通过设定递归深度阈值，超过阈值就退出的方式主动减少递归深度的优化手段。「这种算法成立的前提是」题目中告诉我们答案不超过 xxx」，这样我们可以将 xxx 作为递归深度阈值，这样不仅不会错过正确解，还能在极端情况下有效减少不必须的运算。

具体地，我们可以使用自顶向下的方式记录递归树的层次，和上面介绍如何计算树深度的方法是一样的。接下来在主逻辑前增加「当前层次是否超过阈值」的判断即可。

主代码：

MAX_LEVEL = 20
def dfs(root, level):
    if level > MAX_LEVEL: return
    # 主逻辑
dfs(root, 0)

这种技巧在实际使用中并不常见，不过在某些时候能发挥意想不到的作用。

双向搜索

有时候问题规模很大，直接搜索会超时。此时可以考虑从起点搜索到问题规模的一半。然后将此过程中产生的状态存起来。接下来目标转化为在存储的中间状态中寻找满足条件的状态。进而达到降低时间复杂度的效果。

上面的说法可能不太容易理解。接下来通过一个例子帮助大家理解。

题目地址

https://leetcode-cn.com/problems/closest-subsequence-sum/

题目描述

给你一个整数数组 nums 和一个目标值 goal 。

你需要从 nums 中选出一个子序列，使子序列元素总和最接近 goal 。也就是说，如果子序列元素和为 sum ，你需要 最小化绝对差 abs(sum - goal) 。

返回 abs(sum - goal) 可能的 最小值 。

注意，数组的子序列是通过移除原始数组中的某些元素（可能全部或无）而形成的数组。

 

示例 1：

输入：nums = [5,-7,3,5], goal = 6
输出：0
解释：选择整个数组作为选出的子序列，元素和为 6 。
子序列和与目标值相等，所以绝对差为 0 。
示例 2：

输入：nums = [7,-9,15,-2], goal = -5
输出：1
解释：选出子序列 [7,-9,-2] ，元素和为 -4 。
绝对差为 abs(-4 - (-5)) = abs(1) = 1 ，是可能的最小值。
示例 3：

输入：nums = [1,2,3], goal = -7
输出：7
 

提示：

1 <= nums.length <= 40
-10^7 <= nums[i] <= 10^7
-10^9 <= goal <= 10^9

思路

从数据范围可以看出，这道题大概率是一个时间复杂度的解法，其中 m 是 nums.length 的一半。

为什么？首先如果题目数组长度限制为小于等于 20，那么大概率是一个的解法。

❝
如果这个也不知道，建议看一下这篇文章 https://lucifer.ren/blog/2020/12/21/shuati-silu3/ 另外我的刷题插件 leetcode-cheatsheet 也给出了时间复杂度速查表供大家参考。
❞

将 40 砍半恰好就可以 AC 了。实际上，40 这个数字就是一个强有力的信号。

回到题目中。我们可以用一个二进制位表示原数组 nums 的一个子集，这样用一个长度为的数组就可以描述 nums 的所有子集了，这就是状态压缩。一般题目数据范围是 <= 20 都应该想到。

❝
这里 40 折半就是 20 了。
❞

❝
如果不熟悉状态压缩，可以看下我的这篇文章状压 DP 是什么？这篇题解带你入门
❞

接下来，我们使用动态规划求出所有的子集和。

这也不难求出，转移方程为：dp[(1 << i) + j] = dp[j] + A[i]，其中 j 为 i 的子集，i 和 j 都是数字，i 和 j 的二进制表示的是 nums 的选择情况。

动态规划求子集和代码如下：

def combine_sum(A):
    n = len(A)
    dp = [0] * (1 << n)
    for i in range(n):
        for j in range(1 << i):
            dp[(1 << i) + j] = dp[j] + A[i]
    return dp

接下来，我们将 nums 平分为两部分，分别计算子集和：

n = len(nums)
c1 = combine_sum(nums[: n // 2])
c2 = combine_sum(nums[n // 2 :])

其中 c1 就是前半部分数组的子集和，c2 就是后半部分的子集和。

接下来问题转化为：在两个数组 c1 和 c2中找两个数，其和最接近 goal。而这是一个非常经典的双指针问题，逻辑类似两数和。

只不过两数和是一个数组挑两个数，这里是两个数组分别挑一个数罢了。

这里其实只需要一个指针指向一个数组的头，另外一个指向另外一个数组的尾即可。

代码不难写出：

def combine_closest(c1, c2):
    # 先排序以便使用双指针
    c1.sort()
    c2.sort()
    ans = float("inf")
    i, j = 0, len(c2) - 1
    while i < len(c1) and j >= 0:
        _sum = c1[i] + c2[j]
        ans = min(ans, abs(_sum - goal))
        if _sum > goal:
            j -= 1
        elif _sum < goal:
            i += 1
        else:
            return 0
    return ans

上面这个代码不懂的多看看两数和。

代码

代码支持：Python3

Python3 Code:

class Solution:
    def minAbsDifference(self, nums: List[int], goal: int) -> int:
        def combine_sum(A):
            n = len(A)
            dp = [0] * (1 << n)
            for i in range(n):
                for j in range(1 << i):
                    dp[(1 << i) + j] = dp[j] + A[i]
            return dp

        def combine_closest(c1, c2):
            c1.sort()
            c2.sort()
            ans = float("inf")
            i, j = 0, len(c2) - 1
            while i < len(c1) and j >= 0:
                _sum = c1[i] + c2[j]
                ans = min(ans, abs(_sum - goal))
                if _sum > goal:
                    j -= 1
                elif _sum < goal:
                    i += 1
                else:
                    return 0
            return ans

        n = len(nums)
        return combine_closest(combine_sum(nums[: n // 2]), combine_sum(nums[n // 2 :]))

「复杂度分析」

令 n 为数组长度, m 为。

时间复杂度：
空间复杂度：

BFS

BFS 也是图论中算法的一种。不同于 DFS， BFS 采用横向搜索的方式，从初始状态一层层展开直到目标状态，在数据结构上通常采用队列结构。

具体地，我们不断从队头取出状态，然后「将此状态对应的决策产生的所有新的状态推入队尾」，重复以上过程直至队列为空即可。

注意这里有两个关键点：

将此状态对应的决策。实际上这句话指的就是状态空间中的图的边，而不管是 DFS 和 BFS 边都是确定的。也就是说不管是 DFS 还是 BFS 这个决策都是一样的。不同的是什么？不同的是进行决策的方向不同。
所有新的状态推入队尾。上面说 BFS 和 DFS 是进行决策的方向不同。这就可以通过这个动作体现出来。由于直接将所有「状态空间中的当前点的邻边」放到队尾。由队列的先进先出的特性，当前点的邻边访问完成之前是不会继续向外扩展的。这一点大家可以和 DFS 进行对比。

最简单的 BFS 每次扩展新的状态就增加一步，通过这样一步步逼近答案。其实也就等价于在一个权值为 1 的图上进行 BFS。由于队列的「单调性和二值性」，当第一次取出目标状态时就是最少的步数。基于这个特性，BFS 适合求解一些「最少操作」的题目。

❝
关于单调性和二值性，我会在后面的 BFS 和 DFS 的对比那块进行讲解。
❞

前面 DFS 部分提到了「不管是什么搜索都需要记录和维护状态，其中一个就是节点访问状态以防止环的产生」。而 BFS 中我们常常用来求点的最短距离。值得注意的是，有时候我们会使用一个哈希表 dist 来记录从源点到图中其他点的距离。这个 dist 也可以充当「防止环产生的功能」，这是因为第一次到达一个点后「再次到达此点的距离一定比第一次到达大」，利用这点就可知道是否是第一次访问了。

算法流程

首先将根节点放入队列中。
从队列中取出第一个节点，并检验它是否为目标。

如果找到目标，则结束搜索并回传结果。
否则将它所有尚未检验过的直接子节点加入队列中。

若队列为空，表示整张图都检查过了——亦即图中没有欲搜索的目标。结束搜索并回传“找不到目标”。
重复步骤 2。

算法模板

const visited = {}
function bfs() {
 let q = new Queue()
 q.push(初始状态)
 while(q.length) {
  let i = q.pop()
  if (visited[i]) continue
  for (i的可抵达状态j) {
   if (j 合法) {
    q.push(j)
   }
  }
 }
 // 找到所有合法解
}

常用技巧

双向搜索

题目地址(126. 单词接龙 II)

https://leetcode-cn.com/problems/word-ladder-ii/

题目描述

按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> ... -> sk 这样的单词序列，并满足：

每对相邻的单词之间仅有单个字母不同。
转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。
sk == endWord

给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, ..., sk] 的形式返回。

 

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：[["hit","hot","dot","dog","cog"],["hit","hot","lot","log","cog"]]
解释：存在 2 种最短的转换序列：
"hit" -> "hot" -> "dot" -> "dog" -> "cog"
"hit" -> "hot" -> "lot" -> "log" -> "cog"


示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：[]
解释：endWord "cog" 不在字典 wordList 中，所以不存在符合要求的转换序列。


 

提示：

1 <= beginWord.length <= 7
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有单词 互不相同

思路

这道题就是我们日常玩的「成语接龙游戏」。即让你从 beginWord 开始，接龙的 endWord。让你找到「最短」的接龙方式，如果有多个，则「全部返回」。

不同于成语接龙的字首接字尾。这种接龙需要的是「下一个单词和上一个单词」仅有一个单词不同。

我们可以对问题进行抽象：「即构建一个大小为 n 的图，图中的每一个点表示一个单词，我们的目标是找到一条从节点 beginWord 到节点 endWord 的一条最短路径。」

这是一个不折不扣的图上 BFS 的题目。套用上面的解题模板可以轻松解决。唯一需要注意的是「如何构建图」。更进一步说就是「如何构建边」。

由题目信息的转换规则：「每对相邻的单词之间仅有单个字母不同」。不难知道，如果两个单词的仅有单个字母不同，就「说明两者之间有一条边。」

明白了这一点，我们就可以构建邻接矩阵了。

核心代码：

neighbors = collections.defaultdict(list)
for word in wordList:
    for i in range(len(word)):
        neighbors[word[:i] + "*" + word[i + 1 :]].append(word)

构建好了图。BFS 剩下要做的就是明确起点和终点就好了。对于这道题来说，起点是 beginWord，终点是 endWord。

那我们就可以将 beginWord 入队。不断在图上做 BFS，直到第一次遇到 endWord 就好了。

套用上面的 BFS 模板，不难写出如下代码:

❝
这里我用了 cost 而不是 visitd，目的是为了让大家见识多种写法。下面的优化解法会使用 visited 来记录。
❞


class Solution:
    def findLadders(self, beginWord: str, endWord: str, wordList: List[str]) -> List[List[str]]:
        cost = collections.defaultdict(lambda: float("inf"))
        cost[beginWord] = 0
        neighbors = collections.defaultdict(list)
        ans = []

        for word in wordList:
            for i in range(len(word)):
                neighbors[word[:i] + "*" + word[i + 1 :]].append(word)
        q = collections.deque([[beginWord]])

        while q:
            path = q.popleft()
            cur = path[-1]
            if cur == endWord:
                ans.append(path.copy())
            else:
                for i in range(len(cur)):
                    for neighbor in neighbors[cur[:i] + "*" + cur[i + 1 :]]:
                        if cost[cur] + 1 <= cost[neighbor]:
                            q.append(path + [neighbor])
  以上是关于一文搞定搜索！的主要内容，如果未能解决你的问题，请参考以下文章 
 一文搞定Flutter所有类型导航栏设计
 一文搞定JavaScript的this指向问题
 一文看懂低代码，5分钟从入门到原理全搞定
 什么是接口的幂等性，如何实现接口幂等性？一文搞定
 一文搞定 Mybatis 的应用
 Spring Boot 如果防护 XSS + SQL 注入攻击 ？一文带你搞定！