面试题打卡——C++版

Posted 2021-06-28 ych9527

文章目录

• 把二叉搜索树转换为累加树
• 打家劫舍II
• 最长公共子序列
• 最长递增子序列
• 01矩阵

把二叉搜索树转换为累加树

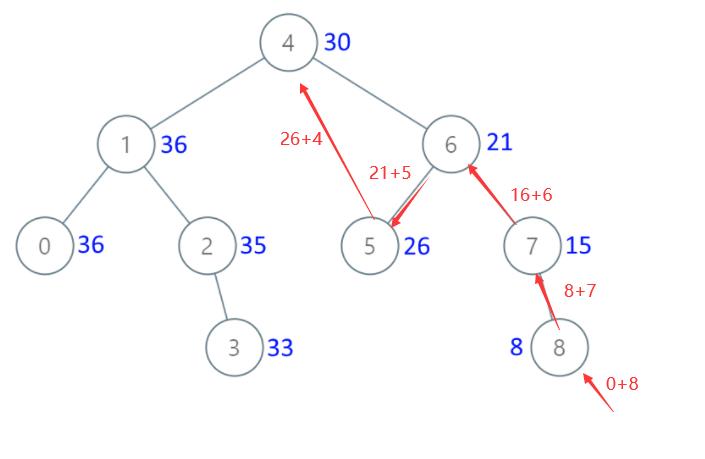
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

题解：

二叉搜索树的特性是 左<根<右 ，现在题目要求，每个节点的值，大于等于原树中的值。
根据二叉树的性质，我们进行 右、根、左的遍历顺序，将前面节点的值加到当前对应的节点即可

class Solution {
public:
    void  _convertBST(TreeNode* root,int &prev)
    {
        if(root==nullptr)
            return;

        _convertBST(root->right,prev);
        root->val+=prev;
        prev=root->val;
        _convertBST(root->left,prev); 
    }
    TreeNode* convertBST(TreeNode* root) {
        int prev=0;
        _convertBST(root,prev);
        return root;
    }
};

打家劫舍II

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

题解：

1.给定三个变量：first表示第两天偷到的钱，second表示前一天偷到的钱，third表示今天偷到的钱

2.很显然，今天偷到的钱 = fmax(昨天偷了，昨天没偷+今天偷的)

3.由于是环形队列，即首尾永远不可能被同时偷，此时我们可以将环形队列拆分成 [0 ,n-1] 和 [1,n]两个队列，再分别计算偷取的总的金额，然后返回较大的值

class Solution {
public:
    int rob(vector<int>& nums) {
        //既然首位不能共存，就将其拆分成两个单独的数组
        // 0~n-1 为一个数组  1-n为一个数组 然后分别在两个数组中进行操作，返回其中的最大值

        int  first=0;
        int second=nums[0];
        int third=nums[0];

        for(int i=1;i<nums.size()-1;i++)
        {
            third=fmax(first+nums[i],second);
            first=second;
            second=third;
        }

        if(nums.size()==1)
            return third;

        first=0;
        second=nums[1];
        int third2=nums[1];
        for(int i=2;i<nums.size();i++)
        {
            third2=fmax(first+nums[i],second);
            first=second;
            second=third2;
        }  

        return fmax(third,third2);      
    }
};

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

题解：

1.定义dp[i][j]表示表示s1的前i个字符和s2的前j个字符中，公共子序列的长度

2.当s1[i]==s2[j]的时候表示，当前位置的字符串是匹配的，那么 dp[i+1][j+1]=dp[i][j] + 1;
**此时表示的含义是：**当前字符匹配，那么dp[i][j]的长度，就为前面的长度+1

3.当s[i]!=s[j]时表示，当前位置的字符是不匹配的，那么 dp[i+1][j+1]=fmax(dp[i+1][j],dp[i][j+1]);
**此时表示的含义是：**当前长度不匹配，那么长度就为s1少一个字符，或者s2少一个字符时候的最长长度，双方同时增加的字符匹配不上，那么就取少一个字符的那个点

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1=text1.size();
        int len2=text2.size();

        vector<vector<int>>dp(len1+1,vector<int>(len2+1,0));
        //dp[i][j]表示text1的前i个字符和text2的前j个字符中，公共子序列的长度

        for(int i=0;i<len1;i++)
        {
            for(int j=0;j<len2;j++)
            {
                if(text1[i]==text2[j])//当前字符匹配上了
                    dp[i+1][j+1]=dp[i][j] + 1;
                else//当前字符没有匹配上
                    dp[i+1][j+1]=fmax(dp[i+1][j],dp[i][j+1]);
            }
        }
        return dp[len1][len2];
    }
};

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

题解：

1.定义一个动态数组dp[i],在nums的i位置时，子序列的长度

2.给定两层循环，外层循环决定dp最终位置，内层循环，表示当前在第j个元素
当nums[i] >nums[j]时，表示是递增的 ，此时dp[i] = fmax(dp[i],dp[j]+1) -> 将i位置前面的所有dp值都看一遍，如果有大的，就可以选择跟再后面

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int>dp(nums.size(),1);
        int max=1;

        for(int i=1;i<nums.size();i++)
        {
            for(int j=0;j<i;j++)
            {
                if(nums[i]>nums[j])
                    dp[i]=fmax(dp[i],dp[j]+1);
                
                max=fmax(max,dp[i]);
            }
        }
        return max;

    }
};

01矩阵

给定一个由 0 和 1 组成的矩阵，找出每个元素到最近的 0 的距离。两个相邻元素间的距离为 1 。

题解：

1.一个位置，到最近0的距离，可以从四个方向选择，我们用一个数组保存每一个格子里面的状态(距离0的位置)

2.遍历两次数组，第一次遍历，求左边的格子和上面格子中，最近的位置+1.第二次遍历，求下边的格子和右边的格子

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        vector<vector<int>>ret(mat.size(),vector<int>(mat[0].size(),INT_MAX-1));

    //用左边和上边的元素求，当前元素
        for(int i=0;i<mat.size();i++)
        {
            for(int j=0;j<mat[0].size();j++)
            {
                if(mat[i][j]==0)
                {
                    ret[i][j]=0;
                    continue;
                }
                else if(i==0&&j==0)
                    continue;
                else if(i==0)//到这里，mat[i][j]肯定不是0
                {
                    ret[i][j]=fmin(ret[i][j],ret[i][j-1]+1);
                }
                else if(j==0)
                {
                    ret[i][j]=fmin(ret[i][j],ret[i-1][j]+1);
                }
                else
                {
                    int left=ret[i][j-1];
                    int up=ret[i-1][j];

                    ret[i][j]=fmin(ret[i][j],fmin(left+1,up+1));
                }
            }
        }
    //用右下的元素进行构造
    int row=mat.size()-1;
    int col=mat[0].size()-1;
    for(int i=row;i>=0;i--)
    {
        for(int j=col;j>=0;j--)
        {
            if(i==row&&j==col)//最右下角
                continue;
            if(ret[i][j]==0||ret[i][j]==1)//当前已经是最小的选择了
                continue;
            if(i==row)
            {
                ret[i][j]=fmin(ret[i][j],ret[i][j+1]+1);
            }
            else if(j==col)
            {

                ret[i][j]=fmin(ret[i][j],ret[i+1][j]+1);
            }
            else
            {
                int right=ret[i][j+1];
                int down=ret[i+1][j];

                ret[i][j]=fmin(ret[i][j],fmin(right+1,down+1));
            }

        }
    }
    return ret;

    }
};