牛客练习赛84：牛客推荐系统开发之标签重复度（点分治+动态开点权值线段树）

Posted 2021-06-28 昵称很长很长真是太好了

题意：

给你一棵树，问树上所有两点路径上的（最大值最小值乘积）之和。
题解：
很明显的一个点分治问题，然后就是个二维偏序问题了（虽然我也不知道啥是二维偏序）。
点分治不难，重点是点分治内cal函数如何去写。

假设当前计算的这个树是以root为根节点，我们对于每一次分治的过程，每个结点储存两个值，一个是从根节点到当前结点路径上的最大值，另一个是最小值记为$ma{x}_{node},mi{n}_{node}$。
对于任意两点，是由这两个点到root的边上的最大值最小值决定的，也就是他们两个点$（x,y）$的乘积实际上是
$min(mi{n}_x,mi{n}_y)\ast max(ma{x}_x,ma{x}_y)$ 得到的。
那么我们考虑如何快速的计算出来经过root点的任意两点的所有答案。
考虑把所有点的最大值和最小值存到一个数组里面，然后按照最小值从小到大进行排序。那么从当前点出发的 到达（另一个点的最小值）都比 当前点的最小值大，所以计算当前点与其他点的值时，我们可以直接用当前点的最小值（$mi{n}_{now}$）计算，
但是这个最小值应该乘一个什么值呢？ 这个时候就需要分情况讨论了，记当前结点的最大值为$ma{x}_{now}$ 对于其他结点的最大值记为$ma{x}_{oth}$，可能比当前结点最大值大，也可能小。
如果大的话那么那个点的贡献值为$ma{x}_{oth}\ast mi{n}_{now}$,如果小的话为$ma{x}_{now}\ast ma{x}_{oth}$
如何完成这个计算呢，我们只要找到有多少个结点的最大值比当前结点的最大值小记为$cnt$，以及比当前结点最大值大的结点之和记为$sum$即可。
公式为：
$cnt\ast ma{x}_{now}\ast mi{n}_{now}+mi{n}_{now}\ast sum$
对于以上查询cnt和sum的操作，我们可以用一个动态开点权值线树进行维护。
然后计算完该点与其他所有点的乘积之后，把该点删掉，防止之后的重复计算。

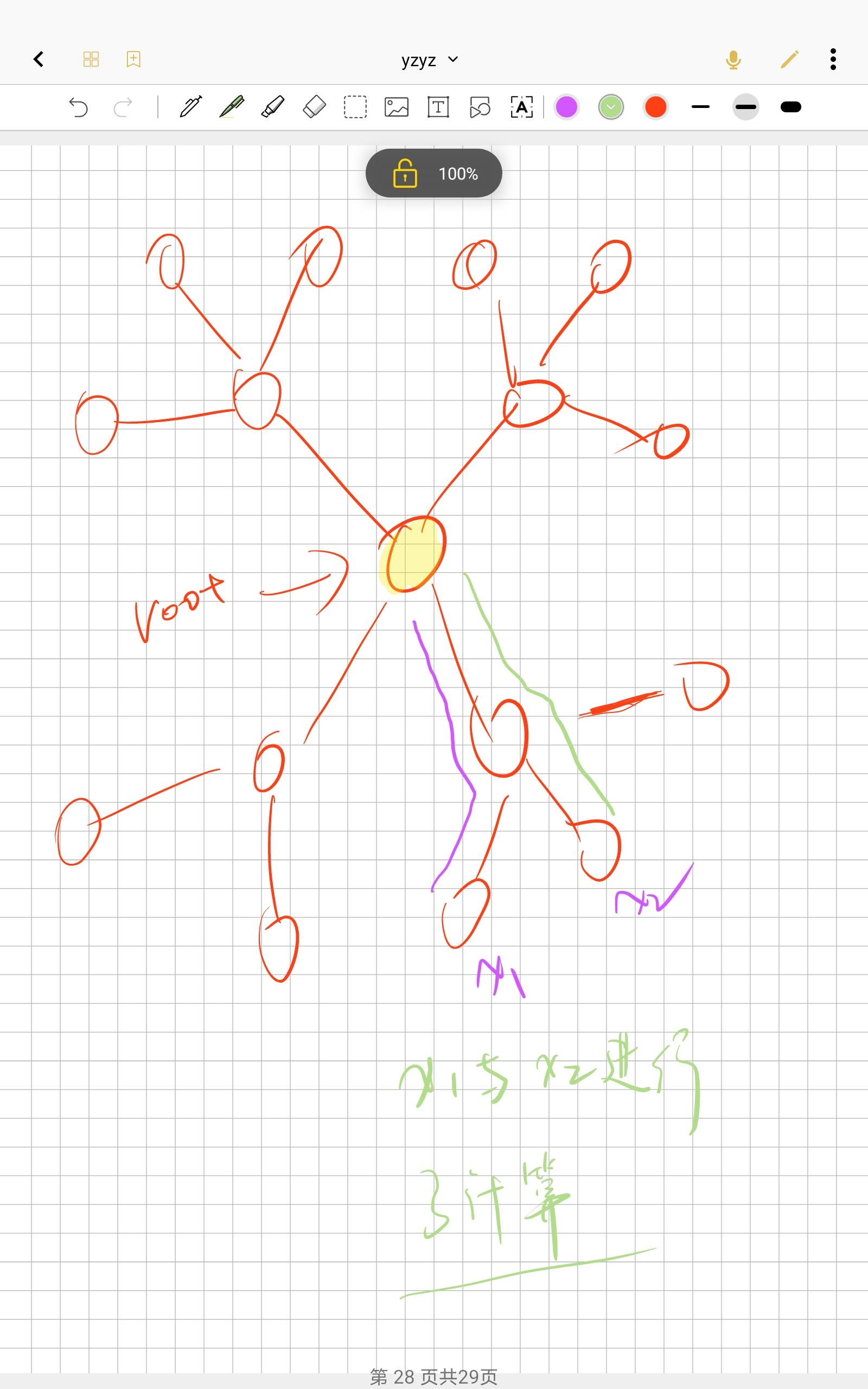
有一个处理的情况（如下图），x1点会与x2点进行了多余的计算。
对于这种情况，我们先不考虑这块多余的计算，计算完后，我们对与多余的计算剪掉即可！

代码：

#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define endl '\\n'
//#define int long long
using namespace std;
const int maxn=1e5+10;
const int mod=998244353;


struct E{
    int to,next;
}edge[maxn*2];
int head[maxn*2],cnt;
int maxp[maxn],sz[maxn];
bool visited[maxn];
int sum,rt;
int n,m;
long long a[maxn],ans=0;
void getrt(int x,int fa){
    sz[x]=1,maxp[x]=0;//maxp初始化为最小值
    //遍历所有儿子，用maxp保留最大大小的儿子大小
    for(int i=head[x];~i;i=edge[i].next){
        int to=edge[i].to;
        //int w=edge[i].w;
        if(to==fa||visited[to]) continue;  //被删掉的也不算
        getrt(to,x);
        sz[x]+=sz[to];
        if(sz[to]>maxp[x]) maxp[x]=sz[to]; //更新maxp
    }
    maxp[x]=max(maxp[x],sum-sz[x]);
    if(maxp[x]<maxp[rt]) rt=x;
}

void add(int u,int v){
    edge[cnt].to=v;
    //edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}


long long tree[maxn*32];
int treecnt[maxn*32];
int ls[maxn*32],rs[maxn*32];
int tot;
void ins(int &node,int start,int ends,int pos,int opt){
    if(!node) node=++tot;
    if(start==ends){
        tree[node]=(tree[node]+pos*opt)%mod;
        treecnt[node]+=1*opt;
        return ;
    }
    int mid=(start+ends)/2;
    if(pos<=mid) ins(ls[node],start,mid,pos,opt);
    else ins(rs[node],mid+1,ends,pos,opt);
    tree[node]=(tree[node]+pos*opt)%mod;
    treecnt[node]+=1*opt;
}
pair<long long,long long> query(int node,int start,int ends,int pos){
    if(ends<=pos){
        return make_pair(tree[node],treecnt[node]);
    }
    int mid=(start+ends)/2;
    //pair<int,int> res(0,0);

    pair<long long,long long> res=query(ls[node],start,mid,pos);

    if(pos>mid){
        auto temp=query(rs[node],mid+1,ends,pos);
        res.first=(res.first+temp.first)%mod;
        res.second=(res.second+temp.second)%mod;
    }
    return res;
}
pair<int,int> v[maxn];
int root,top;
void dfs(int x,int fa,int imin,int imax){
    imin=min(1ll*imin,a[x]);
    imax=max(1ll*imax,a[x]);
    //v.push_back({imin,imax});
    v[++top].first=imin;
    v[top].second=imax;
    ins(root,0,mod,imax,1);
    for(int i=head[x];~i;i=edge[i].next){
        int to=edge[i].to;
        if(to==fa||visited[to]) continue;
        dfs(to,x,imin,imax);
    }
}

//void del(){
//    v.clear();
//}

int cal(int x,int fa,int imin,int imax){
    dfs(x,fa,imin,imax);
    sort(v+1,v+top+1);
    long long res=0;
    //cout<<"afterroot "<<root<<" val "<<tree[root]<<endl;
    for(int i=1;i<=top;i++){
        long long mn=v[i].first;
        long long mx=v[i].second;

        ins(root,0,mod,mx,-1);
        pair<long long,long long> temp=query(1,0,mod,mx);
        //cout<<"mxxx  "<<mx<<endl;
        //cout<<"temp.first "<<temp.first<<" temp.second   "<<temp.second<<endl;
        res=(res+((tree[1]-temp.first)*mn)%mod)%mod;
        res=(res+((temp.second*mx)%mod*mn)%mod)%mod;
        //cout<<"x "<<x<<" "<<res<<endl;
    }
    //cout<<"afterroot "<<root<<" val "<<tree[root]<<endl;
    top=0;
    return res%mod;
    //cout<<summax<<endl;
}

void sol(int x){
    ans=(ans+cal(x,x,a[x],a[x]))%mod;

    for(int i=head[x];~i;i=edge[i].next){
        int to=edge[i].to;
        if(visited[to]) continue;
        ans=(ans-cal(to,x,min(a[x],a[to]),max(a[x],a[to])))%mod;
    }

}

void divide(int x){
    visited[x]=true;  //删除根
    sol(x);  //计算经过根节点的路径

    for(int i=head[x];~i;i=edge[i].next){
        int v=edge[i].to;
        if(visited[v]) continue;
        maxp[rt=0]=sum=sz[v];  //重心设为0，把maxp[0]至为最大值
        getrt(v,0);
        getrt(rt,0);  //与主函数相同
        divide(rt);
    }
}

inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
signed main(){

    memset(head,-1,sizeof head);
    memset(visited,false,sizeof visited);
    n=read();


    sum=n;
    以上是关于牛客练习赛84：牛客推荐系统开发之标签重复度（点分治+动态开点权值线段树）的主要内容，如果未能解决你的问题，请参考以下文章
 
 牛客练习赛83 E.牛客推荐系统开发之标签重复度
 牛客练习赛84 D.牛客推荐系统开发之动态特征获取(set应用)
 牛客练习赛84 C.牛客推荐系统开发之选飞行棋子(状态dp)
 SQL练习题-牛客网
 Python百日刷题计划Day7~牛客题库高效练习
 牛客刷题--SQL篇SQL9查找除复旦大学的用户信息&&SQL10用where过滤空值练习