AtCoder Beginner Contest 205(补题)

Posted 2021-06-28 佐鼬Jun

D - Kth Excluded

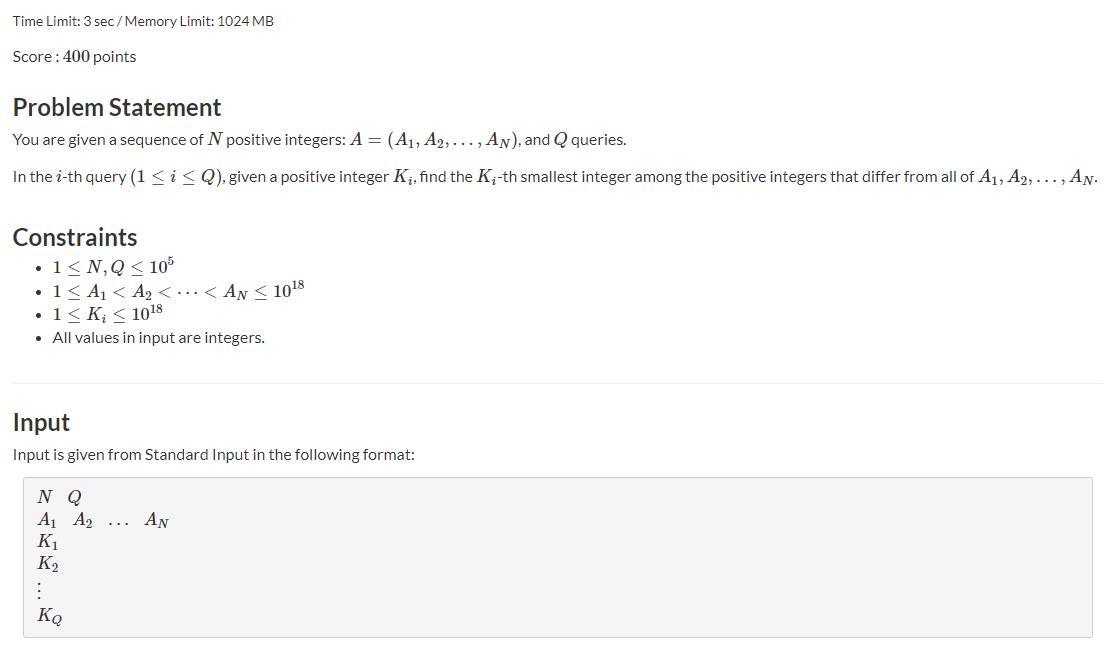
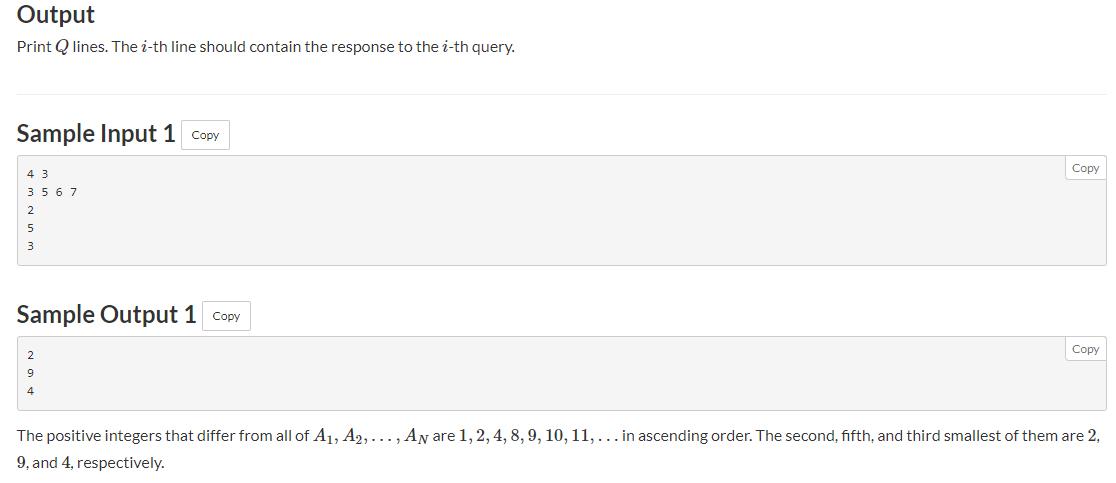
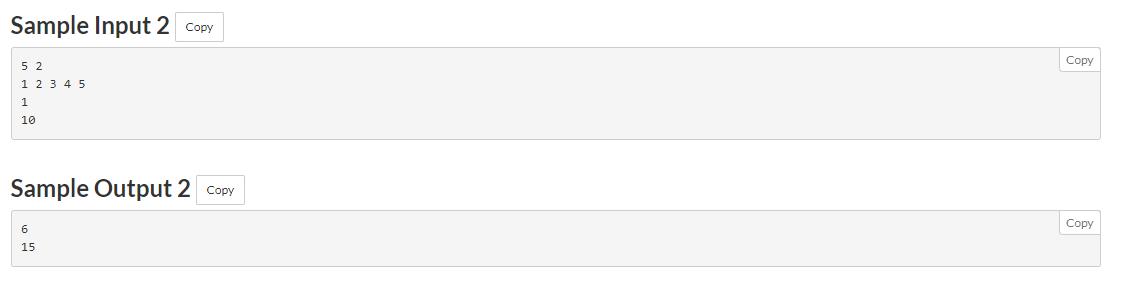
题意： 给n个数，q次询问，每次询问第k大的数（数轴上去掉这n个数后，第k大的数）
思路： 对于这n个数，处理出来，当前这个数前面有多少个数没有被去掉（有多少数在数轴上），然后询问第k个数的时候，就找这个数在那个范围内，找到位置后，就从当前位置往右数k位，就是要找的数。
例如: 样例 3 5 6 7 每个数都存前面有几个数没有被去掉，即 2 3 3 3
要找第三位的时候，明显a[2]=3,符合题意前面有三个数，那这个数就是减去前面存在的数的数量，从3这位数再往后数1个，也就是4，就是答案。
因为你要知道第k个数，你就要先找到符合答案的区间，根据每个数前面有几个数来找，找到区间后，就需要知道上一个数前面有几个数，都去掉后，从上一个数，往后数对应的数量，就是答案。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+10;
int n,q;
ll a[N],k;
int main() {
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) {
        ll x;
        scanf("%lld",&x);
        a[i]=x-i;   
    }
    a[n+1]=1e18+10;
    while(q--) {
        scanf("%lld",&k);
        int l=0,r=n+1;
        while(l<r) {
            int mid=l+r>>1;
            if(k>a[mid]) l=mid+1;
            else r=mid;
        }
        printf("%lld\\n",k+l-1);
        //k-=a[l-1]
        //k+l+a[k-1]
    }
    return 0;
}

E - White and Black Balls

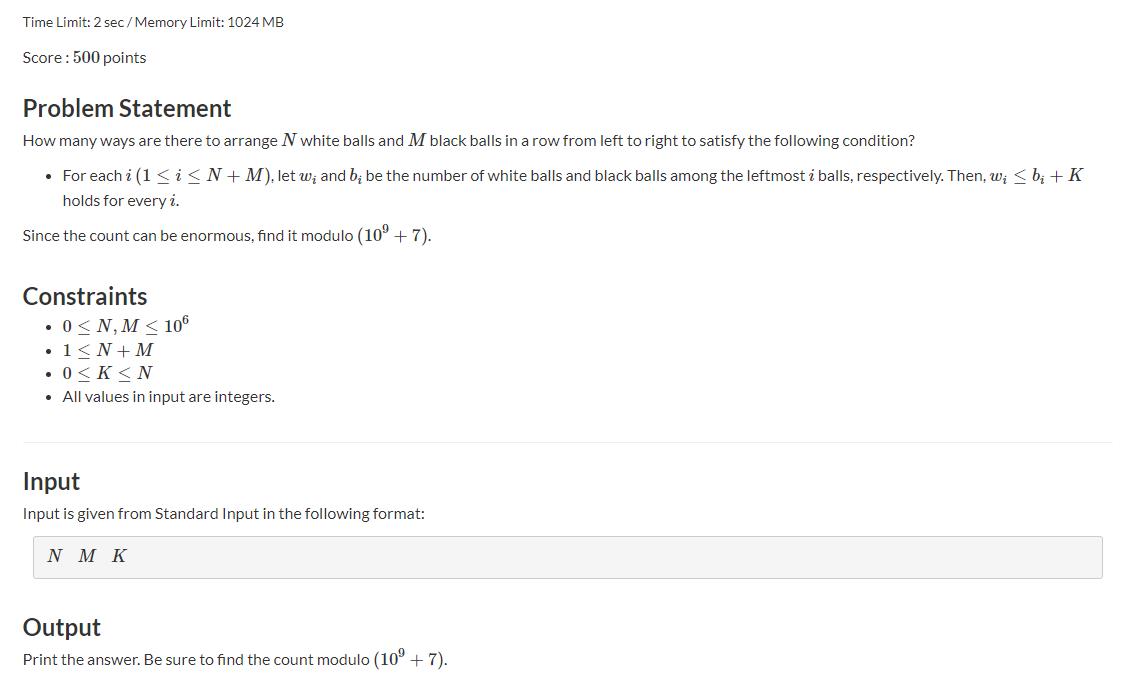
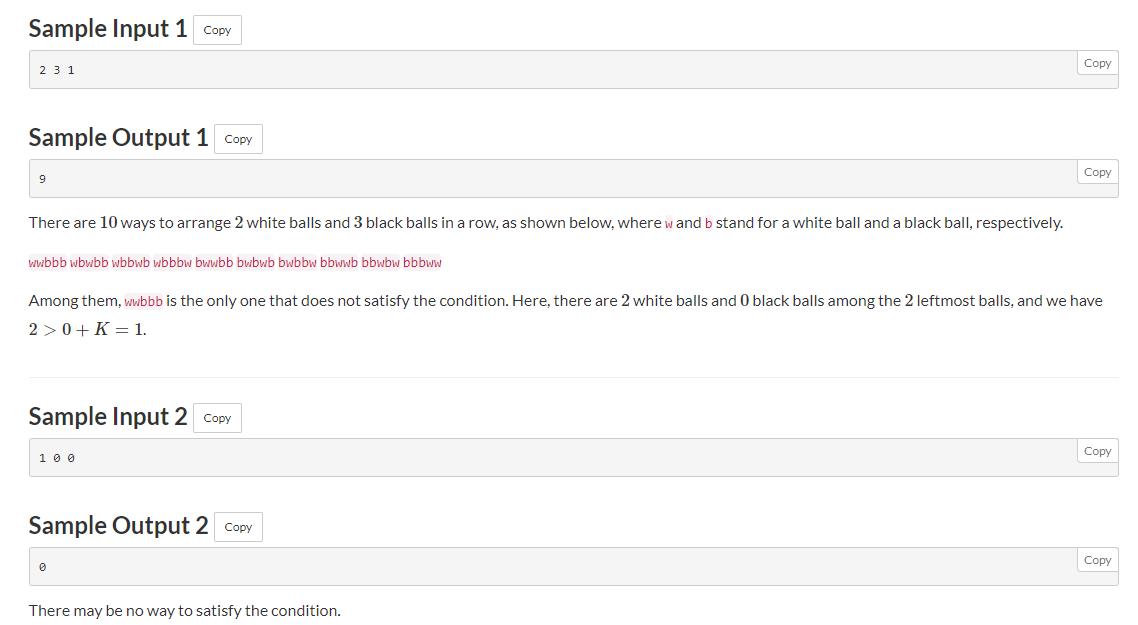
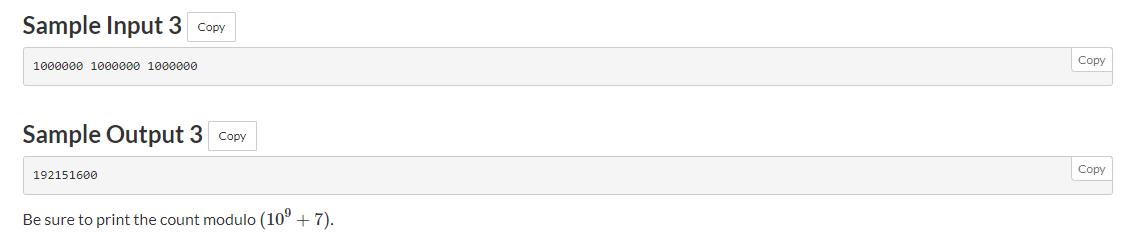
题意： 给N个白球,M个黑球，从左往右排列，但是Wi为从左往右数到第i个位置的白球数量，Bi就是黑球数量，排列时要满足$Wi-Bi<=K$,问有多少种排列方式。
思路： 在坐标轴上，把白球数看成向右走一格，把黑球数看成向上走一格，最终n个白球m个黑球，终点就是$(n,m)$,求解从$(0,0)$到$(n,m)$的合法路径数，合法就代表$Wi-Bi<=K$，求解方式与求卡特兰数如出一辙。

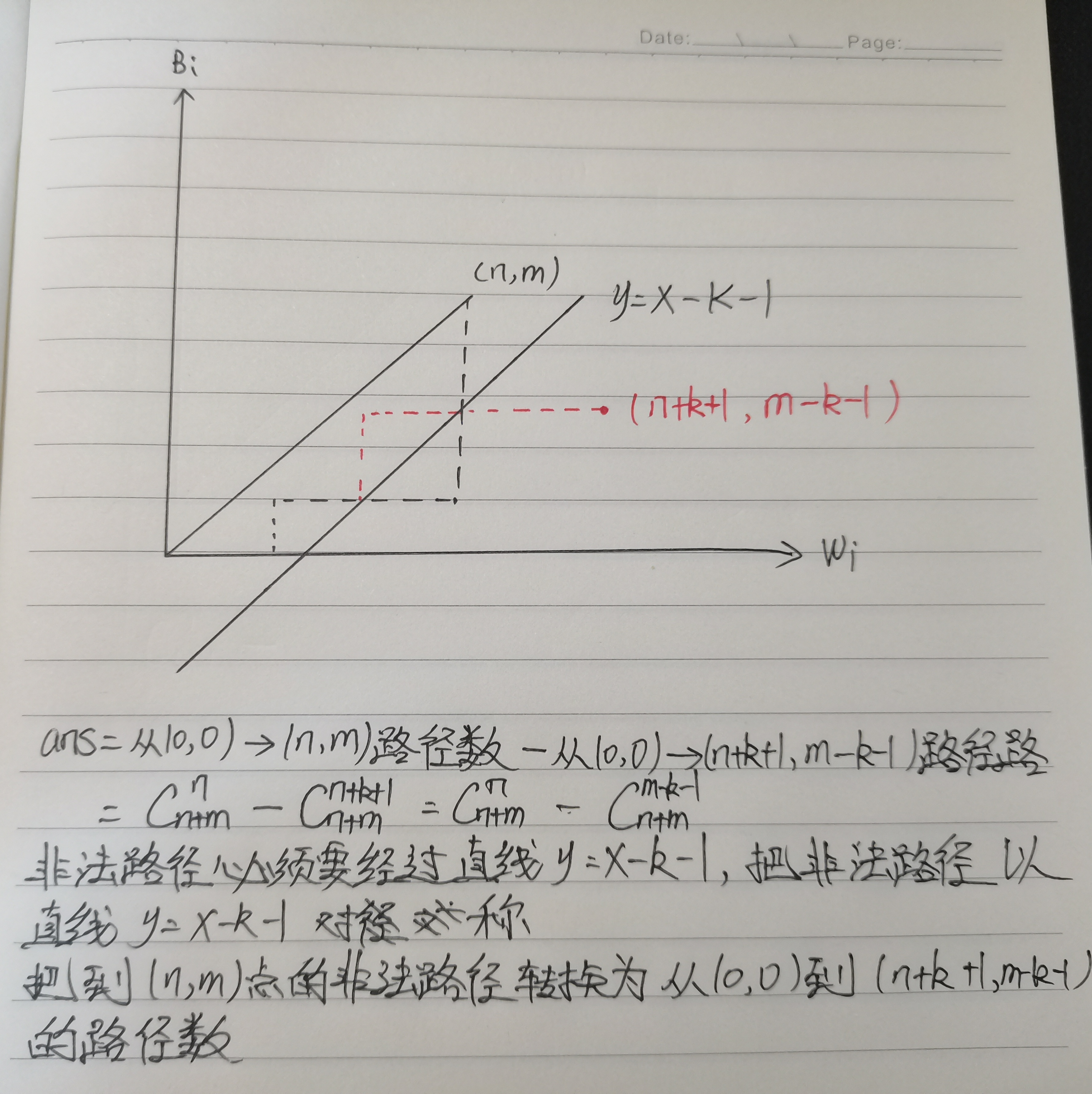
个人感觉此题对于卡特兰数的理解有一定帮助，算是记个小笔记。

最后还要注意，对于两个组合数相减取余问题，要先加个$mod$，再取余$mod$,因为经过取余，后面那个数不一定就比前面小。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e6 + 7;
const int mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int q, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (ll)res * q % p;
        q = (ll)q * q % p;
        k >>= 1;
    }
    return res;
}
void init() {
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i++) {
        fact[i] = (ll)fact[i - 1] * i % mod;
        infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
}

int main() {
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);
    if (n > k + m) {
        cout << 0 << endl;
        return 0;
    }
    init();
    ll a = 0, b = 0;
    a = (ll)fact[n + m] * infact[n] % mod * infact[m] % mod;
    b = (ll)fact[n + m] * infact[n - k - 1] % mod * infact[m + k + 1] % mod;
    printf("%lld\\n", (a - b + mod) % mod);
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
int qmi(int q, int k) {
    int res = 1;
    while (k) {
        if (k & 1) res = (ll)res * q % mod;
        q = (ll)q * q % mod;
        k >>= 1;
    }
    return res;
}
ll get(ll a, ll b) {
    ll res = 1;
    for (int i = a; i > a - b; i--) res = (ll)res * i % mod;
    for (int i = b; i; i--) res = (ll)res * qmi(i, mod - 2) % mod;
    return res;
}
int main() {
    ll n, m, k;
    cin >> n >> m >> k;
    if (m + k < n) {
        cout << 0 << endl;
        return 0;
    }
    ll res1 = get(n + m, n);
    ll res2 = get(n + m, m + k + 1);
    ll res = (res1 - res2 + mod) % mod;
    cout << res << endl;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激