Codeforces Round #725 (Div. 3)（补题）

Posted 2021-06-28 佐鼬Jun

A. Stone Game

Polycarp is playing a new computer game. This game has n stones in a row. The stone on the position i has integer power ai. The powers of all stones are distinct.

Each turn Polycarp can destroy either stone on the first position or stone on the last position (in other words, either the leftmost or the rightmost stone). When Polycarp destroys the stone it does not exist any more.

Now, Polycarp wants two achievements. He gets them if he destroys the stone with the least power and the stone with the greatest power. Help Polycarp find out what is the minimum number of moves he should make in order to achieve his goal.

For example, if n=5 and a=[1,5,4,3,2], then Polycarp could make the following moves:

Destroy the leftmost stone. After this move a=[5,4,3,2];
Destroy the rightmost stone. After this move a=[5,4,3];
Destroy the leftmost stone. After this move a=[4,3]. Polycarp destroyed the stones with the greatest and least power, so he can end the game.
Please note that in the example above, you can complete the game in two steps. For example:

Destroy the leftmost stone. After this move a=[5,4,3,2];
Destroy the leftmost stone. After this move a=[4,3,2]. Polycarp destroyed the stones with the greatest and least power, so he can end the game.
Input
The first line contains an integer t (1≤t≤100). Then t test cases follow.

The first line of each test case contains one integer n (2≤n≤100) — the number of stones.

The second line contains n distinct integers a1,a2,…,an (1≤ai≤n) — the power of the stones.

Output
For each test case, output the minimum number of moves required to destroy the stones with the greatest and the lowest power.

Example
input
5
5
1 5 4 3 2
8
2 1 3 4 5 6 8 7
8
4 2 3 1 8 6 7 5
4
3 4 2 1
4
2 3 1 4
output
2
4
5
3
2
题意： 就是从数组的两边往外拿数，直到把最大数和最小数都拿出来才停止，问最少拿几次
思路： 就那种情况 从左一直往右拿，从右一直往左拿，或者从两边往中间拿，把三种情况都讨论一边就行。

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
const int N=111;
int a[N];
int main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        int n;
        int mi=inf,mx=0;
        scanf("%d",&n);
        int l,r;
        int x;
        for(int i=1;i<=n;i++) {
            scanf("%d",&x);
            if(x==1) l=i;
            if(x==n) r=i;
        }
        if(l<r) printf("%d\\n",min(r,min(n-l+1,n+l-r+1)));
        else {
            printf("%d\\n",min(l,min(n-r+1,r+n-l+1)));
        }
    }
    return 0;
}

B. Friends and Candies

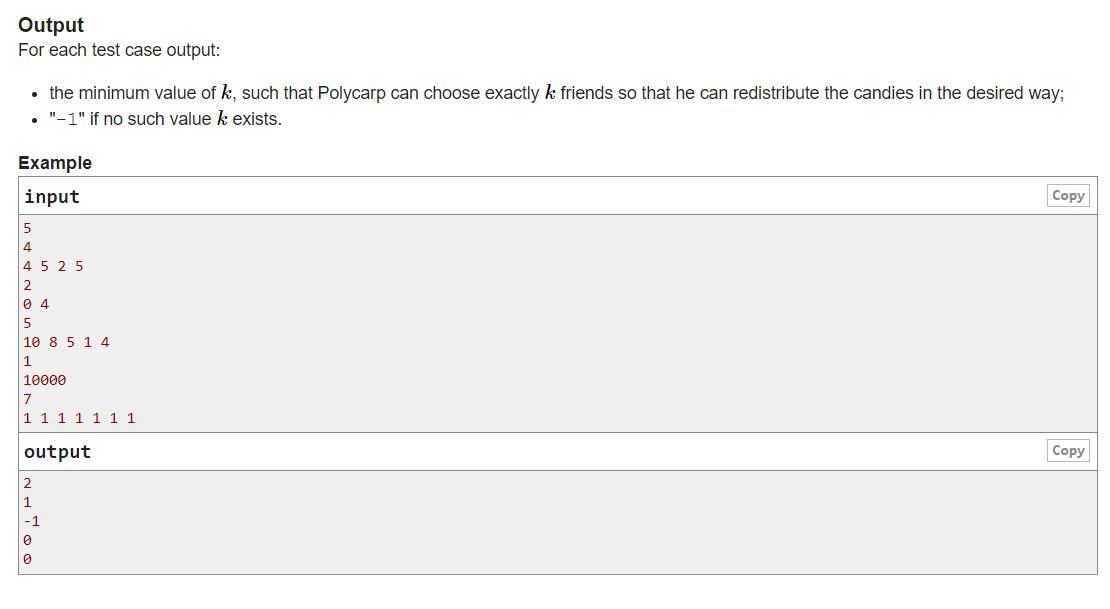
题意： n个人，每个人都有$ai$个糖果，选择k个人，通过把他们的糖果分配给其他人，达成每个人的糖果数量是一样的，问最少选择几个人，如果无法达成，输出’-1’
思路： 总糖果数，如果无法整除n，那就无法平均糖果。
如果可以，就选择那几个糖果数超过平均数的那些人就行。

#include<bits/stdc++.h>
using namespace std;
int t;
#define ll long long
const int N=2e5+10;
int a[N];
int b[N];
int main() {
    scanf("%d",&t);
    while(t--) {
        int n;
        scanf("%d",&n);
        ll sum=0;
        for(int i=1;i<=n;i++) {
            scanf("%d",&a[i]);
            sum+=a[i];
        }
        if(sum%n!=0) {
            printf("-1\\n");
        }
        else {
            int s=sum/n;
            int res=0;
            for(int i=1;i<=n;i++) {
                if(a[i]>s) res++;
            }
            printf("%d\\n",res);
        }
    }
    return 0;
}

C. Number of Pairs

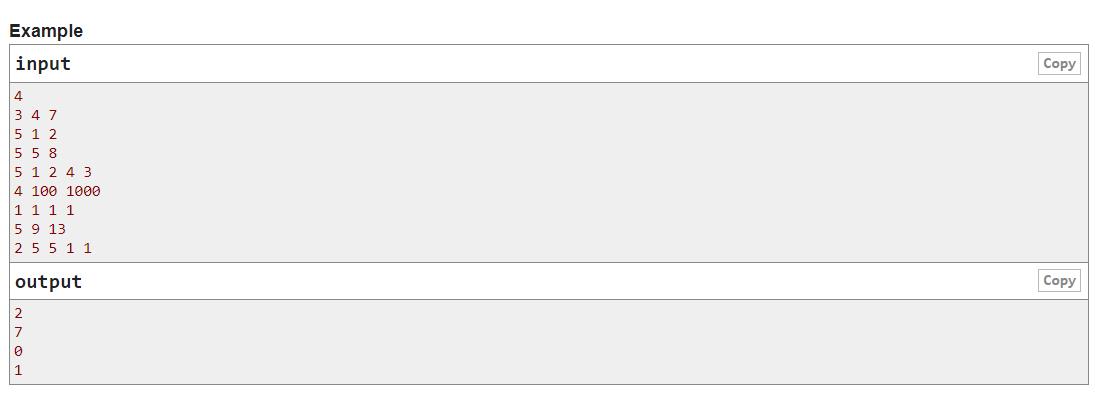
题意： 给一个长度为n的数组，问你有多少对$a[i]+a[j]$满足$l<=a[i]+a[j]<=r$
思路： 利用枚举每个$a[i]$，然后求有多少个$a[j]$,而要求多少个$a[j]$,就相当于是每次枚举一个$a[i]$，都要找数组中有多少个数在$[l-a[i],r-a[i]]$
而这个查询操作，就需要二分来查找，直接用lower_bound( )和upper_bound( )来查找第一个大于等于l-a[i]数的位置，和第一个大于r-a[i]的位置，他们之差，也就是中间的数，就是符合题意的数，还要注意这个题要开long long

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define ll long long
ll a[N];
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        int n;
        ll l, r;
        scanf("%d%lld%lld", &n, &l, &r);
        for (int i = 0; i < n; i++) {
            scanf("%lld", &a[i]);
        }
        sort(a, a + n);
        ll res = 0;
        for (int i = 0; i < n; i++) {
            //枚举每个区间
            res += (upper_bound(a + i + 1, a + n, r - a[i]) -lower_bound(a + i + 1, a + n, l - a[i]));
        }
        printf("%lld\\n", res);
    }
    return 0;
}

D. Another Problem About Dividing Numbers

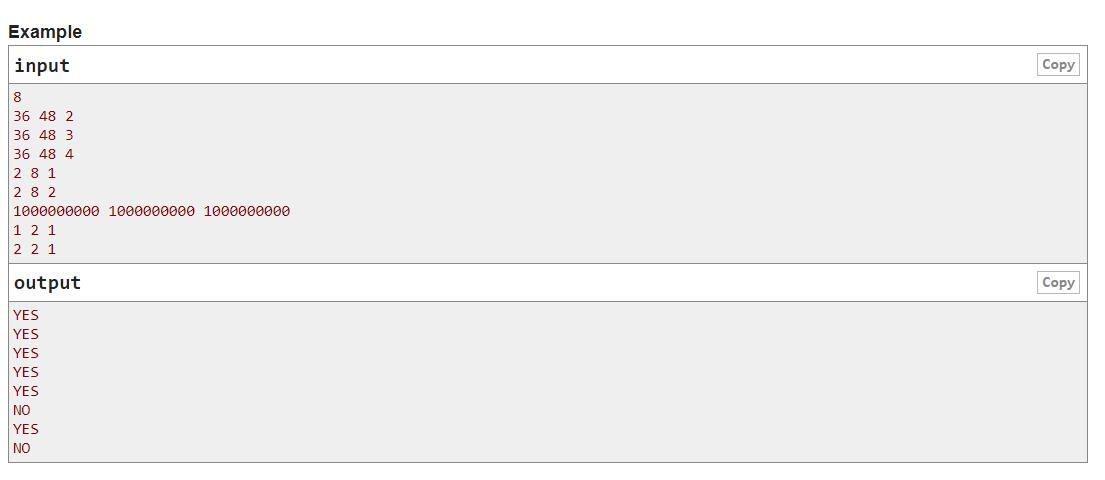
题意： 给定两个整数$a和b$，每次选一个数，除以它的因子，问能否在恰好操作k次，使两个数变成一样的。
思路： 对于两整数$a和b$，操作最多上限right为a和b两个数质因数分解后，质因数的个数。
操作次数的下限left 分三种情况
$1.$$a=b$那就不用操作，操作下限为0
$2.$$gcd(a,b)=a或gcd(a,b)=b$,那只需要将一个数，除以他们的最大公约数，就会相等，所以操作下限为1
$3.$ 剩下的情况操作下限为2，因为把两个数分别除以他们自身，变成1，所以操作下限为1
对于$a=b$的这种情况，只要k不为1，且$k<=right$,那就使YES,否则就是NO
$a!=b$的话，只要k在[left,right]之间，就能成立。

#include <bits/stdc++.h>
using namespace std;

int div(int x) {
    int res = 0;
    for (int i = 2; i * i <= x; i++) { //不能写成i<=x/i，在cf会超时
        if (x % i == 0) {
            int s = 0;
            while (x % i == 0) {
                x /= i, s++;
            }
            res += s;
        }
    }
    if (x > 1) res++;
    return res;
}
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        int a, b, k;
        scanf("%d%d%d", &a, &b, &k);
        int right = div(a) + div(b);
        int d = __gcd(a, b);
        int left;
        if (a == b)
            left = 0;
        else if (d == a || d == b)
            left = 1;
        else
            left = 2;
        if (left == 0) {
            if (k <= right && k != 1) {
                puts("YES");
            } else
                puts("NO");
        } else if (k <= right && k >= left) {
            puts("YES");
        } else {
            puts("NO");
        }
    }
    return 0;
}

F. Interesting Function

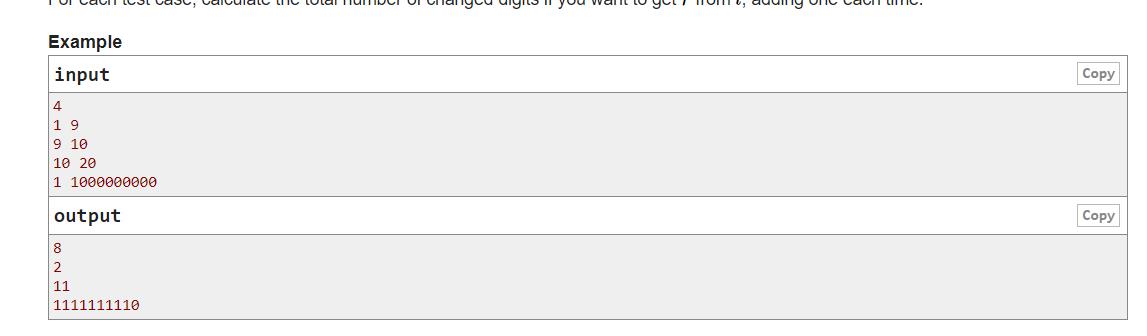
题意： 给定一个数$l$，每次$+1$，直到变成$r$，在每次$+1$操作会有n位数改变，问最后l变成r后，把每次n位数改变，所有的n加起来，输出最后的和
思路： 如果$l和r$是个位数，那么$l->r$的转变对个位的贡献就是1，最后累加总贡献就是$r-l$
如果$l和r$是10位数,每次+1，对个位数的贡献度是1，但对十位数的贡献就是$\frac{r}{10}$$-$$\frac{l}{10}$
依次往下推,对第$i$位数的贡献度就是$\frac{r}{10的i次方}$$-$$\frac{l}{10的i次方}$，$i从0开始$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll solve(int x) {
    ll res=0;
    while(x) {
        res+=x;
        x/=10;
    }
    return res;
}
int main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        ll l,r;
        scanf("%lld%lld",&l,&r);
        ll res=solve(r)-solve(l);
        printf("%lld\\n",res);
    }
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激