线段树 信息维护 单点修改你能回答这些问题吗
Posted 鱼竿钓鱼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线段树 信息维护 单点修改你能回答这些问题吗相关的知识,希望对你有一定的参考价值。
【线段树 信息维护 单点修改】你能回答这些问题吗

思路
1单点修改,只需要pushup。
2查询:查询区间内最大连续子段和
一、维护哪些信息
思考:查询区间内最大连续子段和需要存哪些信息
基本的
struct Node{
int l,r;//区间左右端点
int tmax;//最大连续子段和
}
但是我们无法通过左右儿子的tmax得到父节点的tmax。有可能横跨左右子区间。
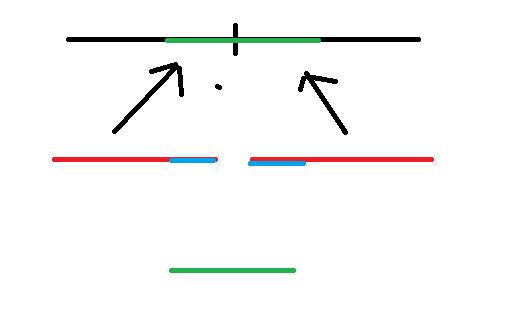
可以发现
横跨左右子区间的最大连续子段和=左子区间的最大后缀和右子区间的最大前缀
所以我们还需对维护每个区间的最大后缀和以及最大前缀和
struct Node{
int l,r;//区间左右端点
int tmax;//最大连续子段和
int lmax,rmax;//最大前缀和,最大后缀和
}
那么我们可以得到tmax的表达式
t
m
a
x
=
m
a
x
(
l
e
f
t
s
o
n
t
m
a
x
,
r
i
g
h
t
s
o
n
t
m
a
x
,
l
e
f
t
s
o
n
r
m
a
x
+
r
i
g
h
t
s
o
n
l
m
a
x
)
tmax=max(left_{son} tmax,right_{son}tmax,left_{son}rmax+right_{son}lmax)
tmax=max(leftsontmax,rightsontmax,leftsonrmax+rightsonlmax)
继续思考新增的信息能否通过左右子区间得到。
父区间的最大前缀和可以有左右子区间最大前缀和得到吗
1最大前缀和只在左区间,那么可以得到
2最大前缀和横跨左右区间,光凭目前的信息无法得到。
我们可以发现横跨左右区间的最大前缀和可以表示为左区间的sum+右区间最大前缀和。
所以我们还要维护一个sum
struct Node{
int l,r;//区间左右端点
int tmax;//最大连续子段和
int lmax,rmax;//最大前缀和,最大后缀和
int sum;//区间和
}
我们可以得到lmax的表达式
l
m
a
x
=
m
a
x
(
l
e
f
t
s
o
n
l
m
a
x
,
l
e
f
t
s
o
n
s
u
m
+
r
i
g
h
t
s
o
n
l
m
a
x
)
lmax=max(left_{son}lmax,left_{son}sum+right_{son}lmax)
lmax=max(leftsonlmax,leftsonsum+rightsonlmax)
同理我们可以得到rmax的表达式
r
m
a
x
=
m
a
x
(
r
i
g
h
t
s
o
n
r
m
a
x
,
r
i
g
h
t
s
o
n
s
u
m
+
l
e
f
t
s
o
n
r
m
a
x
)
rmax=max(right_{son}rmax,right_{son}sum+left_{son}rmax)
rmax=max(rightsonrmax,rightsonsum+leftsonrmax)
继续检查新增信息sum可不可以由左右子区间得到,发现可以,那么维护信息足够了。
s
u
m
=
l
e
f
t
s
o
n
s
u
m
+
r
i
g
h
t
s
o
n
s
u
m
sum=left_{son}sum+right_{son}sum
sum=leftsonsum+rightsonsum
总结一下线段树找到要维护信息的流程
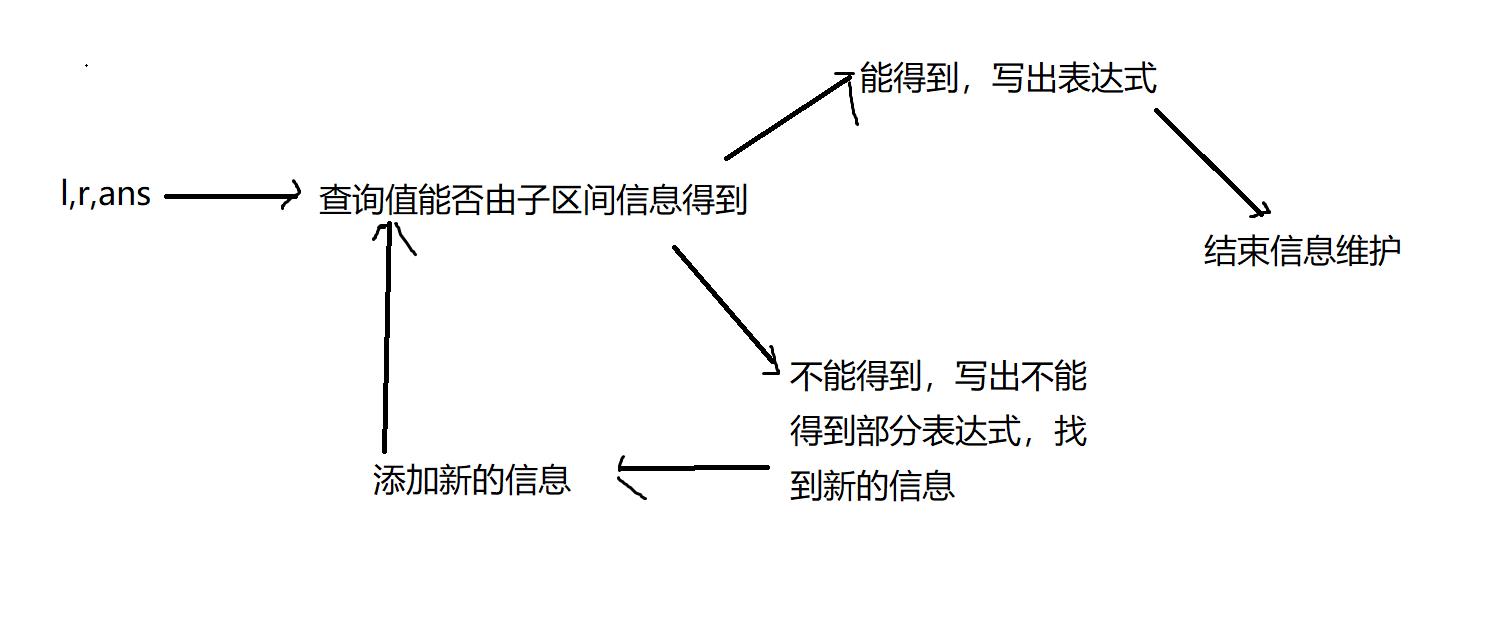
二、写代码!
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int n,m;
int w[N];
struct Node{
int l,r;
int tmax;
int lmax,rmax;
int sum;
}tr[N*4];
/*维护更新信息*/
void pushup(Node &u,Node &l,Node &r){
u.sum=l.sum+r.sum;
u.lmax=max(l.lmax,l.sum+r.lmax);
u.rmax=max(r.rmax,r.sum+l.rmax);
u.tmax=max(l.rmax+r.lmax,max(l.tmax,r.tmax));
}
void pushup(int u){
pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r){
if(l==r)tr[u]={l,r,w[r],w[r],w[r],w[r]};//叶子节点
else{
tr[u]={l,r};//别忘记
int mid=(l+r)>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);//递归左右区间
pushup(u);
}
}
void modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x)tr[u]={x,x,v,v,v,v};//叶子节点
else{
int mid=(tr[u].l+tr[u].r)>>1;
if(x<=mid)modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
Node query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r)return tr[u];//区间被包含
else{
int mid=(tr[u].l+tr[u].r)>>1;
if(r<=mid)return query(u<<1,l,r);
else if(l>mid)return query(u<<1|1,l,r);
else{
auto left=query(u<<1,l,r);
auto right=query(u<<1|1,l,r);
Node res;
pushup(res,left,right);//合并左右子区间答案
return res;
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&w[i]);
build(1,1,n);
int k,x,y;
while(m--){
scanf("%d%d%d",&k,&x,&y);
if(k==1){
if(x>y)swap(x,y);
printf("%d\\n",query(1,x,y).tmax);
}
else modify(1,x,y);
}
return 0;
}
以上是关于线段树 信息维护 单点修改你能回答这些问题吗的主要内容,如果未能解决你的问题,请参考以下文章