动态规划之最长公共子串

Posted 2021-06-27 快乐江湖

文章目录

• 题目
• 解题思路
• 动态规划
• 代码

题目

牛客

解题思路

这道题属于动态规划中十分经典的题目。
题目的意思不用再做解释了，我们可以让两个字符串分别作为一个二维矩阵的行和列，然后比较二维矩阵中每个点对应的行列字符串中的字符是否相同，如果相同设置为1，否则设置为0.接着只需要查找值为1的最长对角线就可以解决

对于题目中给定的两个字符串

str1="asdfas"
str2="werasdfaswer"

分别以列行和行构造二维矩阵如下

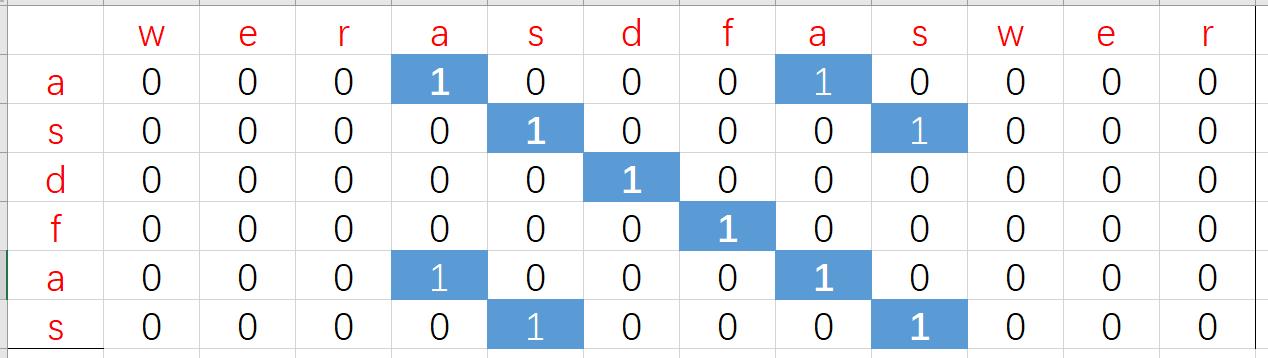
可以发现其中存在很多公共子串，但是最长的公共子串就是对角线最长的那一个

动态规划

如果每次重复求肯定效率不过，所以动态规划的核心就是如何转移，如何利用上一步的结果，根据当前的条件判断，得出现在状态的结果

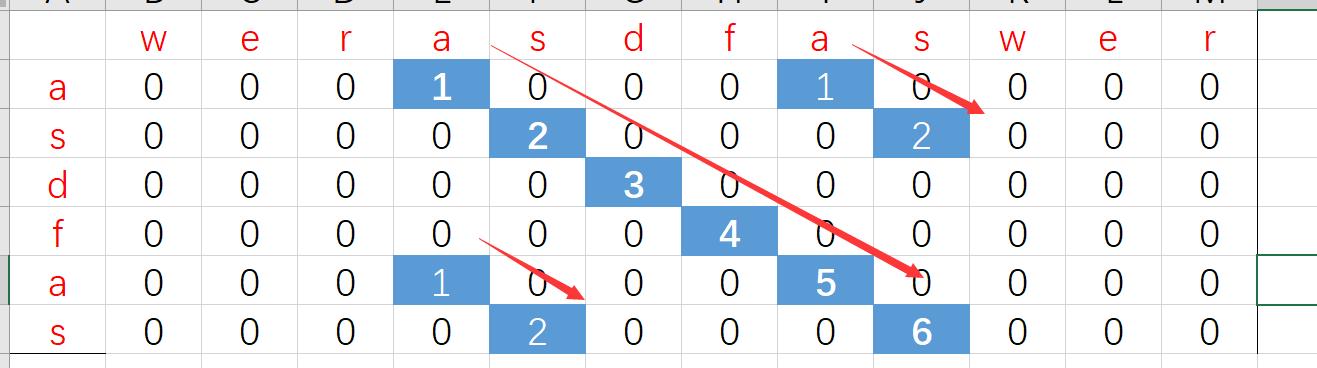
所以我们可以再计算某个二维矩阵的元素的值的时顺便保存下电气概念最长的公共子串的长度，也就是状态变化为

record[i][j]=1可以演变为record[i][j]=1+record[i-1][j-1]

代码

#include <iostream>
#include <vector>
using namespace std;

int maxcom_substr(const string& str1,const string& str2)
{
    int len1=str1.size();
    int len2=str2.size();
    vector<vector<int>> martix(len1,vector<int>(len2,0));
    int max_len=0;
    
    for(int i=0;i<len1;i++)
    {
        for(int j=0;j<len2;j++)
        {
            if(str1[i]==str2[j])
            {
                if(i>=1 && j>=1)//防止越界
                    martix[i][j]=1+martix[i-1][j-1];
                else
                    martix[i][j]=1;//特殊处理i=0，j=0
            }
            if(martix[i][j] > max_len)//有变化就修改
                max_len=martix[i][j];
        }
    }
    return max_len;
    
}

int main()
{
    string str1,str2;
    while(cin >> str1 >> str2)
    {
        int max_len=maxcom_substr(str1,str2);
        cout<<max_len<<endl;
    }
    
    return 0;
    
}