基于Matlab实现退化图像的逆滤波处理

Posted 2021-06-27 博主QQ2449341593

　图像复原的方法很多，常用的比较经典的是反向滤波法和约束还原法。博主在做反向滤波实验的过程中，发现图像复原的关键是退化模型的建立，可以夸张地说：要有好的复原效果就得根据各个图像的退化特点建立相关的退化模型，并在退化模型的基础上做相关的滤波或者说对待处理的像素做相应的处理，从而尽可能地复原图像。再说一遍，复原方法的关键是退化模型。可以想到的是，由于造成图像退化的原因五花八门。简单的有加性退化、减性、乘性、除性退化等；复杂的有非线性退化等。从这一点看来似乎没有通用的复原方法，这样一来似乎只能使用深度学习等智能算法做一些通用复原算法的研究了。博主推荐在使用神经网络等算法进行研究之前，先修《数据分析与数据挖掘》和《复杂性思维》，或许能从中找到通用复原算法的钥匙！

实验内容　　

　　利用逆滤波和其他逆卷积算法对运动模糊或散焦模糊图像进行图像复原，并给出实现结果。

【背景知识】

1. 图像退化模型

　　图形复原处理的关键是建立退化模型，原图像f(x,y)是通过一个系统H及加入一个外来加性噪声n(x,y)而退化成一幅图像g(x,y)的。

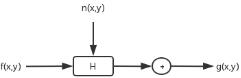
　　这样图像的退化过程的数学表达式就可以写为g(x,y)=H[f(x,y)]+n(x,y)。容易想到图像退化及复原的过程如下：

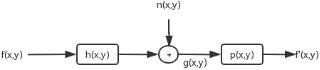
　　如果系统H满足下面两个式子，那么系统就是线性和空间位置不变的系统。在图像复原处理中，非线性和空间变化的系统的模型虽然更具普遍性和准确性，但它却给处理工作带来巨大的困难，它常常没有解或很难用计算机来处理。实际的成像系统在一定条件下往往可以近似地视为线性和空间不变的系统，因此在图像复原处理中，往往用线性和空间不变的系统模型加以近似地视为线性和空间不变的系统。

      　

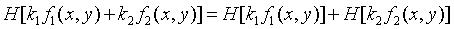
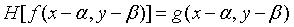
2.连续的退化模型

　　线性系统H可由其冲激响应来表征，当系统H空间位置不变时，则 h(x-α,y-β)=H[δ(x-α,y-β)]。系统H对输入f(x,y)的响应就是系统输入信号f(x,y)与系统冲激响应的卷积。考虑加性噪声n(x,y)时。可写为：

　　　　　　　　　　　　　　　　

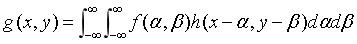
　　其中n(x,y)与图像中位置无关。

3.离散的退化模型

　　如果给出 A×B 大小的数字图像，以及 C×D 大小的点扩散函数，可首先扩展大小为 M×N 的周期延拓图像。

　　   

 

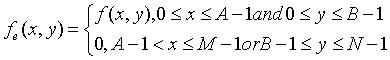
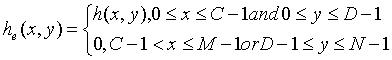
　　为避免折叠，要求 M≥A+C-1，N≥B+D-1。这样一来，fe(x,y)和he(x,y)分别成为二维周期函数，它们在x和y方向上的周期分别为M和N。由此得到二维退化模型为一个二维卷积形式：
　　

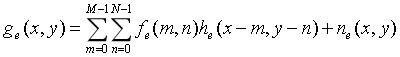
 　　式中，x=0,1,2,3，…，M-1；y=0,1,2，…，N-1；ge(x,y)也为周期函数，其周期与fe(x,y)和he(x,y)完全一样。上式也可用矩阵表示为 g=Hf+n。G(u,v)、F(u,v)和N(u,v)分别是g(x,y)、f(x,y)和n(x,y)的二维傅里叶变换。于是有G(u,v)=MNH(u,v)F(u,v)+N(u,v)。这样就将求f(x,y)的过程转换为求解F(u,v)的过程，简化了计算过程，同时上式也是进行图像复原的基础。

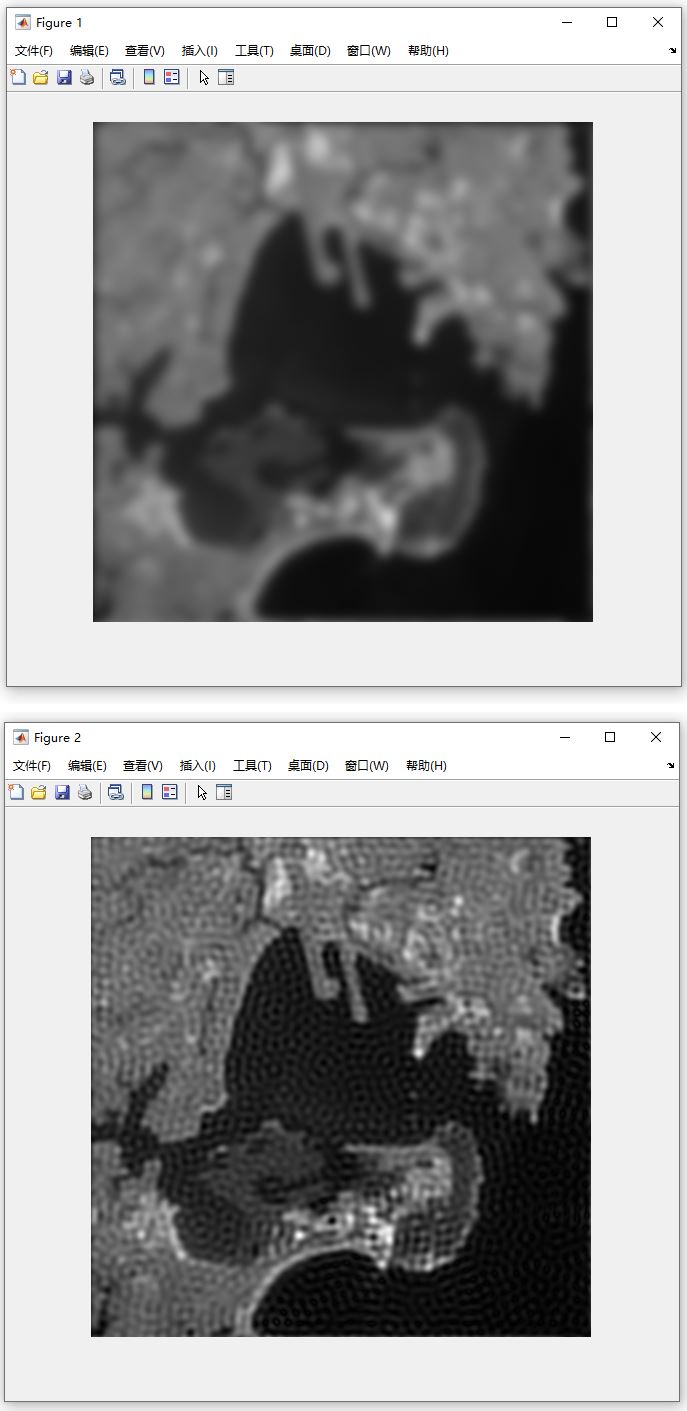
文件列表：目录│文件列表:

 ├ 1.源码

 │  │ NiLvBo.m

 │  └ satellite_degraded.tiff

代码下载https://www.cnblogs.com/matlabxiao/p/14883637.html