HashMap红黑树原理及源码分析---图形注释一应俱全
Posted lllllLiangjia
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了HashMap红黑树原理及源码分析---图形注释一应俱全相关的知识,希望对你有一定的参考价值。
目录
一、红黑树定义
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点,这类节点不可以忽视,否则代码会看不懂)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(黑色平衡)。
NIL节点:为了红黑树平衡而添加的空节点
二、节点新增原理:
新插入节点默认是红色,如果是黑色的话那么当前分支上就会多出一个黑色节点出来,从而破坏了黑色平衡。
- 如果插入的是第一个节点(根节点),红色变黑色。
- 如果父节点为黑色,则直接插入,不需要变色。
- 如果父节点是红色,没有叔叔节点或者叔叔节点是黑色,则以爷爷节点为支点旋转,旋转之后原来的爷爷节点变红色,原来的父节点变黑色。
- 如果父节点为红色,叔叔节点也是红色(此种情況爷爷节点一定是黑色),则父节点和叔叔节点变黑色,爷爷节点变红色(如果爷爷节点是根节点,则再变成黑色),爷爷节点此时需要递归(把爷爷节点当做新插入的节点再次进行比较)。
三、红黑树的生成
2.1 一个节点
当插入一个元素为5的节点时,由于是新插入的节点,所以应该是红色。但是该树只有一个节点,也就是root根节点,根据红黑树定义2可得,该节点变为黑色。

2.2 两个节点
当已经有一个根节点插入第二个节点元素为x时,分为两种情况。当x>5时,该节点为右节点。当x<5时,该节点为左节点。

2.3 三个节点
在已存在的两个节点产生的这两种情况来看,再添加一个元素,会有以下6种情况
2.3.1 第二个节点作为root右子树情况下
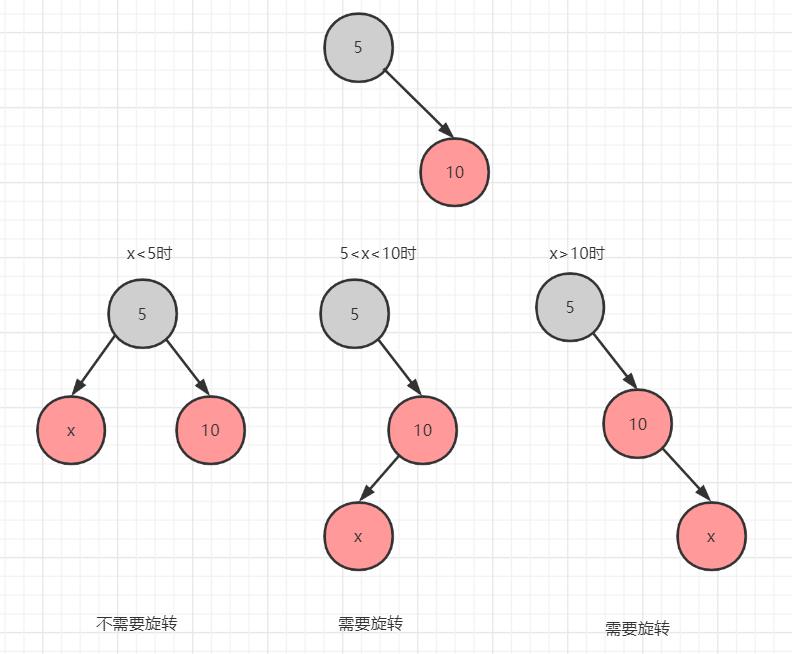
2.3.2 第二个节点作为root左子树情况下
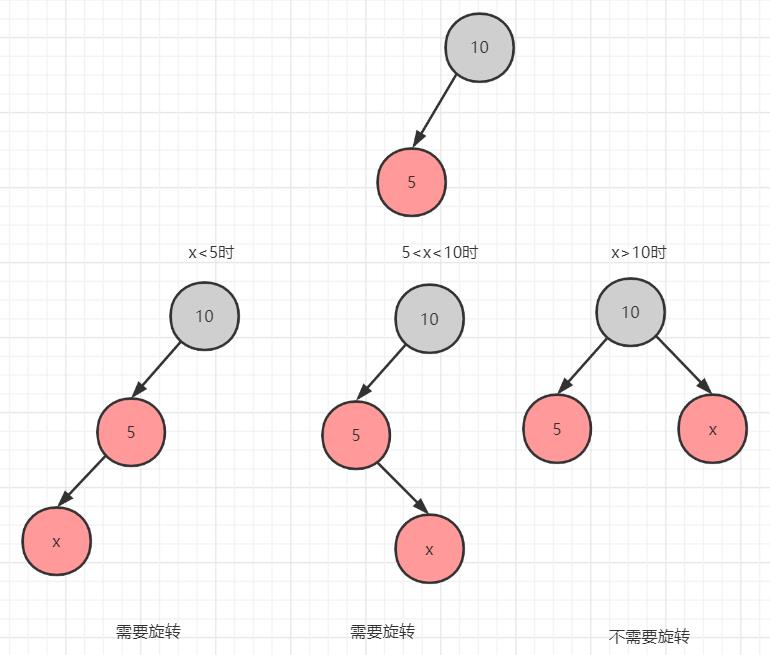
上面存在的六种情况,由于其中两种已经是平衡的红黑树所以不需要旋转。其余的四种情况我们要进一步分析,如何旋转才能让他成为红黑树。
四、左旋和右旋
4.1 左旋

左旋:以某个节点作为旋转点,其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点,左子节点保持不变。
4.2 右旋

右旋:以某个节点作为旋转点,其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变。
五、四种情况分析
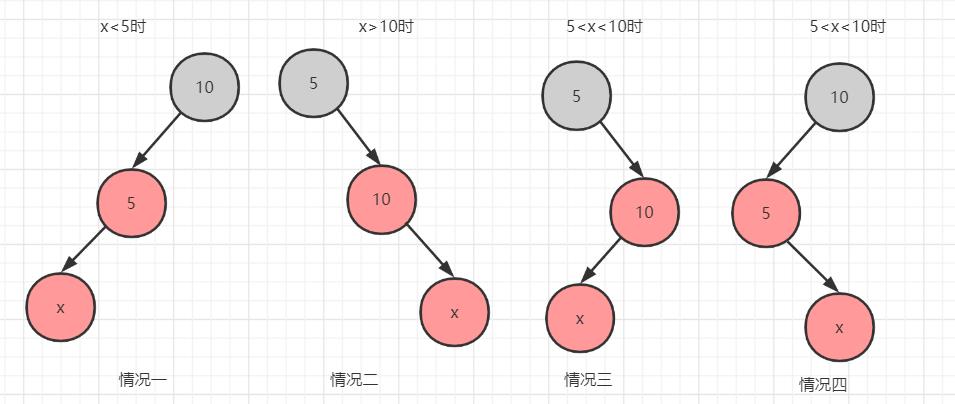
5.1 情况一变红黑树
由图可知,明显该树左边太重了,所有的节点都是左子树,那我们应该向右旋转。以元素为10的节点为旋转点,左子节点5变成他的父节点。左子节点5的右子节点变为旋转节点的左子节点,由于是NIL节点所以在此不再画出。然后进行变色。

5.2 情况二变红黑树
由图可知,情况二的树右边太重了,所有的节点都是右子树,那我们应该向左旋转。以元素为5的节点为旋转点,右子节点10变成他的父节点。右子节点10的左子节点变为旋转节点的右子节点,由于是NIL节点所以在此不再画出。然后进行变色。

5.3 情况三变红黑树
如图所示,情况三刚开始我们无法判定是向左旋还是向右旋。那我们就看他的部分子树,元素10节点和元素x节点如果向右旋转生成的树结构那是不是就和情况二一样了。此时节点为5的右子树为x节点,x节点右子树是元素为10的节点。这就与情况二一样了,再通过左旋并变色处理变成红黑树。

5.4 情况四变红黑树
如图所示,元素5的节点和元素x节点先进行左旋,然后整个树结构与情况一一样,再进行右旋,并进行变色处理,就成为了一个红黑树。

5.5 总结
- 以上情况都是在节点新增原理的前三条基本原理基础上进行分析的。
- 无论一个红黑树的节点多少,深度多大,当它新增节点的时候,发生颜色冲突,如果符合节点新增原理的第四条那就无需旋转,只要变色就可以成为新的红黑树。其它需要旋转才能解决的场景都是以上四种情况的变形。
- 红黑树的形成有两个阶段:成为二叉搜索树和旋转变色。
六、源码分析
6.1 链表转换为半成品树
当满足散列表上的一条链表节点数大于等于8时会进入treeifyBin(tab, hash)方法
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 散列表为空或者长度小于64时
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
// 散列表进行扩容操作
resize();
// 否则将链表转换为半成品树(这些树节点由前指针相连)
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
// 根据Node节点创建新的TreeNode节点
TreeNode<K,V> p = replacementTreeNode(e, null);
// 尾指针为null时,说明树还未创建
if (tl == null)
// 头指针赋值给第一个树节点
hd = p;
else {
// 新插入的树节点的前指针指向上一个尾节点
p.prev = tl;
// 尾节点指向新插入的树节点
tl.next = p;
}
// 尾指针指向最新插入的树节点
tl = p;
} while ((e = e.next) != null); // 遍历下一个节点
// 半成品树的头指针赋值给散列表对应位置
if ((tab[index] = hd) != null)
// 转换为红黑树
hd.treeify(tab);
}
}由上可知,节点转换为红黑树的两个条件:
- 链表节点数大于等于8
- 散列表长度大于等于64
6.2 半成品树转换为红黑树
treeify(Node<K,V>[] tab)方法就可以分为先成为一个二叉搜索树,再调用balanceInsertion(root, x)方法通过旋转变色成为红黑树。
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
// 遍历循环半成品树节点
for (TreeNode<K,V> x = this, next; x != null; x = next) {
// 头节点指针的下一个节点是第一个树节点
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
// 当没有根节点的时候,创建根节点,并成黑色
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
// 否则不是根节点的时候
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 遍历已经存在的树节点
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
// 所遍历的树节点hash值大于要插入的节点hash值,向左子树继续遍历
if ((ph = p.hash) > h)
dir = -1;
// 所遍历的树节点hash值小于要插入的节点hash值,向右子树继续遍历
else if (ph < h)
dir = 1;
// 如果要插入的节点hash值等于遍历所在节点hash,但是key不等时,此事发生hash冲突
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
//说明红黑树中没有与之相等的 那就必须进行插入操作。
// 分出插入节点是左节点还是右节点
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
// 根据dir区分要继续遍历左节点还是右节点
// 当下一个节点为null的时候说明已经找到要插入的树节点所在的位置
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 要插入的树节点父指针 指向 调整成树后遍历所得树节点
x.parent = xp;
// 根据dir区分出插入节点放入左节点还是右节点
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 插入完成后是一个新树,需要变色或旋转成为红黑树
root = balanceInsertion(root, x);
break;
}
}
}
}
// 检验root节点是不是第一个节点
moveRootToFront(tab, root);
}6.3 二叉搜索树变成红黑树
这里是从叶节点遍历到root根节点,从部分到整体一步步满足红黑树的条件。新插入的节点根据是父节点的左子树还是右子树,以及父节点、爷爷节点和叔叔节点的颜色可以分为不同的情况,根据不同的情况分别进行左旋和右旋。
rotateLeft(TreeNode<K,V> root,TreeNode<K,V> p)是进行左旋转。
rotateRight(TreeNode<K,V> root,TreeNode<K,V> p)是进行右旋转。
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 此处就是节点新增原理提到的新插入节点默认为红色
x.red = true;
// 遍历树x节点一直到root节点
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 如果是根节点
if ((xp = x.parent) == null) {
// 变为黑色
x.red = false;
return x;
}
//如果该节点父节点是黑色,或者父节点为根节点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 如果父节点是爷爷节点的左子树
if (xp == (xppl = xpp.left)) {
// 如果叔叔节点不为空并且是红色
// xpp
// / \\
// xp(R) Red
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 如果叔叔节点为空或者不为空是黑色
else {
// 如果该节点是右节点
// xpp xpp
// / \\ /
// xp(R) black xp(R)
// \\ \\
// x(R) x(R)
if (x == xp.right) {
// 左旋
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 如果该节点是左节点
// xpp xpp
// / \\ /
// xp(R) black xp(R)
// / /
// x(R) x(R)
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
// xpp(R) xpp(R)
// / \\ /
// xp(B) black xp(B)
// / /
// x(R) x(R)
// 右旋将的到的新树赋给root,再次遍历
root = rotateRight(root, xpp);
}
}
}
}
// 如果父节点是爷爷节点的右子树
else {
// 如果叔叔节点不为空并且是红色
// xpp
// / \\
// Red xp(R)
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
// 如果叔叔节点为空或者不为空是黑色
else {
// 如果该节点是左节点
// xpp xpp
// \\ / \\
// xp(R) black xp(R)
// / /
// x(R) x(R)
if (x == xp.left) {
// 右旋
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 如果该节点是右节点
// xpp xpp
// \\ / \\
// xp(R) black xp(R)
// \\ \\
// x(R) x(R)
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
// xpp(R) xpp(R)
// \\ / \\
// xp(B) black xp(B)
// \\ \\
// x(R) x(R)
// 左旋
root = rotateLeft(root, xpp);
}
}
}
}
}
}6.4 旋转
我根据源码将不同的情况下的左旋或右旋结果,用注释表示了出来。大家可以与第五节那四种情况结合分析。
6.4.1 左旋
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
if (p != null && (r = p.right) != null) {
// p的右节点指向r的左孩子(即rl),如果rl不为空,其父节点指向p;
// p
// \\
// r
// /
// rl
if ((rl = p.right = r.left) != null)
rl.parent = p;
// r
// /
// p
//------------------------------------
// p节点为根节点,直接root指向r,同时颜色置为黑色(根节点颜色都为黑色)
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
// 如果该节点是右节点
// pp pp
// / \\ /
// p(R) black p(R)
// \\ \\
// r(R) r(R)
else if (pp.left == p)
pp.left = r;
// 走完该方法图形后的
// pp pp
// / \\ /
// r(R) black r(R)
// / /
// p(R) p(R)
//---------------------------------
// pp pp
// \\ \\
// p(R) p(R)
// \\ / \\
// r(B) black r(B)
// \\ \\
// x(R) t x(R)
else
pp.right = r;
// 走完该方法后的图形
// pp pp
// \\ \\
// r(B) r(B)
// / \\ / \\
// p(R) x(R) p(R) x(R)
// /
// black
r.left = p;
p.parent = r;
}
return root;
}6.4.2 右旋
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
// p的左节点指向l的右孩子(即lr),如果lr不为空,其父节点指向p;
// p
// /
// l
// \\
// lr
if ((lr = p.left = l.right) != null)
lr.parent = p;
// l
// \\
// p
//------------------------------------
// 如果pp为null,说明p节点为根节点,直接root指向l,同时颜色置为黑色(根节点颜色都为黑色)
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
// pp pp
// \\ / \\
// p(R) black p(R)
// / /
// l(R) l(R)
else if (pp.right == p)
pp.right = l;
// 走完该方法后的图形
// pp pp
// \\ / \\
// l(R) black l(R)
// \\ \\
// p(R) p(R)
// --------------------------------------
// pp(B) pp(B)
// / /
// p(R) p(R)
// / \\ /
// l(B) black l(B)
// / /
// x(R) x(R)
else
pp.left = l;
// 走完该方法后的图形
// pp(B) pp(B)
// / /
// l(B) l(B)
// / \\ / \\
// x(R) p(R) x(R) p(R)
// \\
// black
l.right = p;
p.parent = l;
}
return root;
}6.5 插入新节点
插入新节点从root节点往下遍历分为4种情况:
- 要插入的节点hash值小于遍历所在节点hash,遍历左子树
- 要插入的节点hash值大于遍历所在节点hash,遍历右子树
- 要插入的节点hash值等于遍历所在节点hash,并且key值相等返回该节点
- 要插入的节点hash值等于遍历所在节点hash,但是key不等时,发生hash冲突。此时又分为两种情况。
- 遍历该节点的左右子节点是否存在hash相等,并且key也相等的节点,有则返回该节点
- 如果没有则调用tieBreakOrder(k, pk)方法,比较key值,确定是遍历左子树还是右子树
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
// 获取根节点
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;
// 如果要插入的节点hash值小于遍历所在节点hash,遍历左子树
if ((ph = p.hash) > h)
dir = -1;
// 如果要插入的节点hash值大于遍历所在节点hash,遍历右子树
else if (ph < h)
dir = 1;
// 如果要插入的节点hash值等于遍历所在节点hash,并且
// key值相等返回该节点
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
// 如果要插入的节点hash值等于遍历所在节点hash,但是key不等时,此时发生hash冲突
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
// 在左右子树递归的寻找 是否有key的hash相同 并且equals相同的节点
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
// (ch = p.left) != null 左子树不为空
// (ch = p.right) != null 右子树不为空
// (q = ch.find(h, k, kc)) != null) 递归查找hash值相等的并且key也相等
// 如果找到hash值相等的则返回该节点
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
//说明红黑树中没有与之相等的 那就必须进行插入操作。
// 分出插入节点是左节点还是右节点
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
// 如果dir小于0,那p等于p的左子树节点,不为null则继续遍历
// 如果dir大于0,那p等于p的右子树节点,不为null则继续遍历
// 当为null时说明是叶子节点则执行下面方法
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
// 由于TreeNode继承了Node,创建一个新的TreeNode节点将要插入的
// hash、key、value存入
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
// dir小于0,新节点为左节点
if (dir <= 0)
xp.left = x;
// dir大于0,新节点为右节点
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
// balanceInsertion(root, x)方法让一个树成为红黑树,并返回根节点
// moveRootToFront,检验root节点是不是第一个节点
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
以上是关于HashMap红黑树原理及源码分析---图形注释一应俱全的主要内容,如果未能解决你的问题,请参考以下文章