背包DP(数位成本和为目标值的最大数字+完全平方数+零钱兑换+盈利计划+最后一块石头的重量+目标和+1和0）

Posted 2021-06-27 秦枫-_-

example 1:

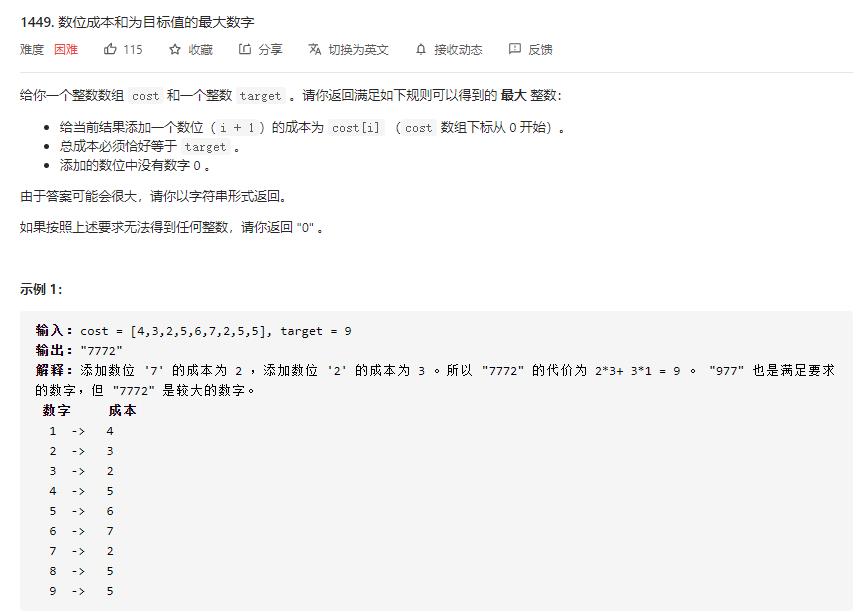
class Solution {
    public String largestNumber(int[] cost, int target) {
     int [][]dp=new int[10][target+1];
     for(int i=0;i<=target;i++){
         dp[0][i]=Integer.MIN_VALUE;
     }
     int [][]form=new int[10][target+1];
     dp[0][0]=0;
     for(int i=1;i<=9;i++){
         for(int j=0;j<=target;j++){
             if(j<cost[i-1]){
             dp[i][j]=dp[i-1][j];
             form[i][j]=j;
             }
             else{
              if(dp[i-1][j]>dp[i][j-cost[i-1]]+1){
                  dp[i][j]=dp[i-1][j];
                  form[i][j]=j;
              }
              else{
                  dp[i][j]=dp[i][j-cost[i-1]]+1;
                  form[i][j]=j-cost[i-1];
              }
             }
         }
     }
     if(dp[9][target]<0)return "0";
     StringBuffer res=new StringBuffer();
     int i=9,j=target;
     while(i>0){
         if(j==form[i][j])i--;
         else{
             res.append(i);
             j=form[i][j];
         }
     }
     return res.toString();
    }
}

example 2:

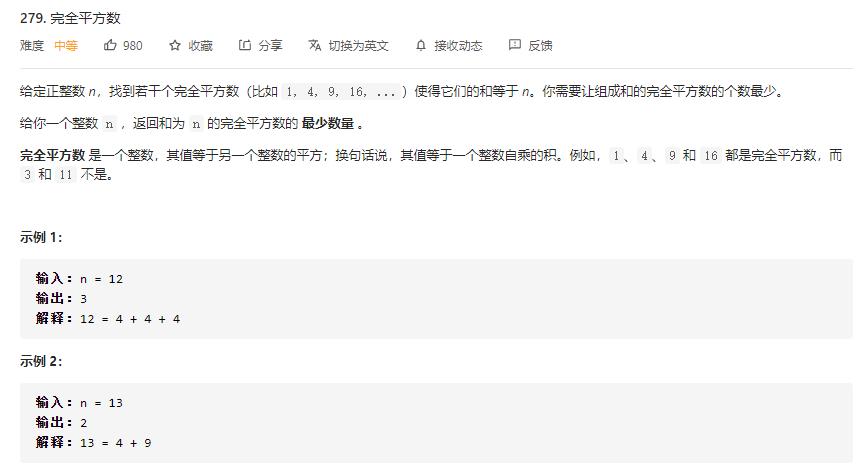
class Solution {
    public int numSquares(int n) {
    int []dp=new int[n+1];
    for(int i=1;i<=n;i++){
    int minn = Integer.MAX_VALUE;
        for(int j=1;j*j<=i;j++){
            minn = Math.min(minn, dp[i - j * j]);
        }
        dp[i]=minn+1;
    }
    return dp[n];
    }
}

**example 3：**零钱兑换

class Solution {
    public int change(int amount, int[] coins) {
    int []dp=new int[amount+1];
    dp[0]=1;
    for(int i=1;i<=coins.length;i++){
        for(int j=coins[i-1];j<=amount;j++){         
                dp[j]+=dp[j-coins[i-1]];       
        }
    }
    return dp[amount];
    }
}

example 4：

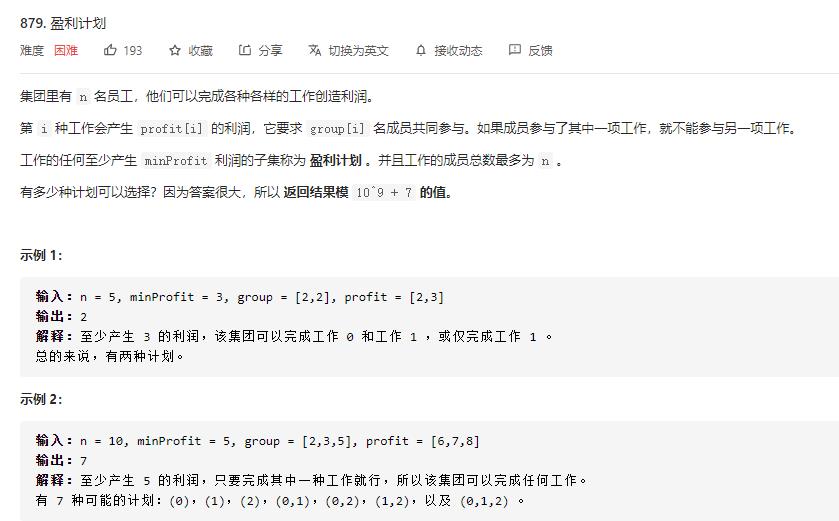
class Solution {
    public int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {
    int mod=(int)Math.pow(10,9)+7;
    int [][][]dp=new int[profit.length+1][n+1][minProfit+1];
    dp[0][0][0]=1;
    for(int i=1;i<=profit.length;i++){
        for(int j=0;j<=n;j++){
            for(int k=0;k<=minProfit;k++){
                dp[i][j][k]=dp[i-1][j][k];
                if(group[i-1]<=j)dp[i][j][k]=(dp[i][j][k]+dp[i-1][j-group[i-1]][Math.max(0,k-profit[i-1])])%mod;
            }
        }
    }
    int res=0;
    for(int i=0;i<n+1;i++){
        res=(res+dp[profit.length][i][minProfit])%mod;
    }
    return res;
    }
}

问题转化为：
我们可以吧石头分成两堆，一堆是重量较大的，一堆重量较小，那么每次从两堆石头中各挑选一个石头相撞，撞剩下的石头放回原堆，那么怎么使得最后剩下的石头重量最小？

首先考虑一个问题：
较大的那一堆石头重量大于较小的那一堆，设较小的重量为neg，另一堆重量则是sum-neg，如此得出sum-neg>=neg,neg<=sum/2,当neg=sum/2的时候剩余最后一块一定是0重量，那么只要使得背包容量从sum/2递减到0，找出能满足题中给出的石头和能不能满足背包容量，能即为答案，进而转化为背包的目标和问题。

因此我们设定一个背包容量0-sum/2，看能否装满，所以每到一个石头如果装他，就去看有没有装满j-stones[i-1]这个容量，如果前面的石头能装成这个容量如果不装，就需要看前i-1是否已经装满了 j 容量，最后只要反向查找出满足题中数组的最大目标和为多少？即可得出最后的答案

class Solution {
    public int lastStoneWeightII(int[] stones) {
     int sumall=0;
     for(int i=0;i<stones.length;i++){
         sumall+=stones[i];
     }
     int sum=sumall;
     sumall/=2;//分成两堆石头 互相碰，小的碰没了大的碰完再放回去，结果就等于两堆石头差，这个差值>=0,由此推导出小的那堆石头<=sumall/2
     boolean [][]dp=new boolean[stones.length+1][sumall+1];
     dp[0][0]=true;
     for(int i=1;i<=stones.length;i++){
         for(int j=0;j<=sumall;j++){
             dp[i][j]=dp[i-1][j];
             if(j>=stones[i-1])dp[i][j]=dp[i-1][j]||dp[i-1][j-stones[i-1]];//设定一个背包容量看能否装满，所以每到一个石头如果装他，就去看有没有装满j-stones[i-1]这个容量，如果不装，就需要看前i-1是否已经装满了j容量
         }
     }
     for(int i=sumall;i>=0;i--){//找出最大的j结果就等于总和减-2*j
         if(dp[stones.length][i])return sum-2*i;
     }
     return 0;
    }
}

example 5：

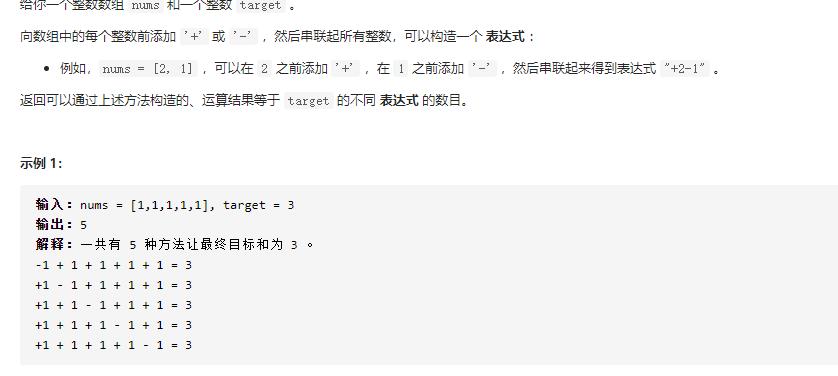
同上面问题一样：
我们设添加负号的数的和为neg，正好的数和则为sum-neg，那么问题就转化为了sum-neg-neg=target，即neg=（sum-target）/2的方案数，由此我们转化成目标和等于neg的方案数问题，sum和target都是已知量

我们设定一个dp[i][j]前i个数目标和为j的方案数
所以每次遇到一个数，都有要不要选他的问题，选他的方案数=dp [i-1] [j-nums[i]] ,不选他的方案数dp[i-1][j]，所以若num[i]>j,不能选i这个数，num[i]<=j则方案数=两者相加

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sumall=0;
        for(int i=0;i<nums.length;i++){
            sumall+=nums[i];
        }

     int dif=sumall-target;
     if(dif<0||dif%2==1)return 0;
     dif/=2;
     int [][]dp=new int[nums.length+1][dif+1];
     dp[0][0]=1;
     for(int i=1;i<=nums.length;i++){
         for(int j=0;j<=dif;j++){
             dp[i][j]=dp[i-1][j];
             if(j>=nums[i-1])dp[i][j]+=dp[i-1][j-nums[i-1]];
         }
     }
     return dp[nums.length][dif];
    }
}

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
       int [][][]dp=new int[strs.length+1][m+1][n+1];
       for(int i=1;i<=strs.length;i++){
           int[]count=countzeroandone(strs[i-1]);
           for(int j=0;j<=m;j++){
               for(int k=0;k<=n;k++){
                   dp[i][j][k]=dp[i-1][j][k];
                   if(j>=count[0]&&k>=count[1])
                   dp[i][j][k]=Math.max(dp[i-1][j][k],dp[i-1][j-count[0]][k-count[1]]+1);
               }
           }
       }
       return dp[strs.length][m][n];
    }
    public int []countzeroandone(String s){
        int []res=new int[2];
        for(char ch:s.toCharArray()){
            res[ch-'0']++;
        }
        return res;
    }
}