速看，双100%剑指 Offer 14- I. 剪绳子 I

Posted 2021-06-27 来老铁干了这碗代码

立志用最少的代码做最高效的表达

---

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：
2 <= n <= 58

---

解法一：DP

class Solution {
    public int cuttingRope(int n) {
        // 动态规划特点：问题最优解、局部最优解、不会计算重复子问题。
        // 通过自下而上的方式避免计算重复子问题。

        // 为什么这里要这么设置？
    /*解决大问题的时候用到小问题的解并不是这三个数
    真正的dp[1] = 0,dp[2] = 1,dp[3] = 2
    但是当n=4时，4=2+2 2*2=4 而dp[2]=1是不对的
    也就是说当n=1/2/3时，分割后反而比没分割的值要小，当大问题用到dp[j]时，说明已经分成了一个j一个i-j，这两部分又可以再分，但是再分不能比他本身没分割的要小，如果分了更小还不如不分
    所以在这里指定大问题用到的dp[1],dp[2],dp[3]是他本身*/
        if(n == 2) return 1;    // 分割成1*1（n>1）
        if(n == 3) return 2;    // 分割成1*2

        int[] dp = new int[n+1];
        dp[0] = 0; dp[1] = 1; dp[2] = 2; dp[3] = 3;
        for(int i = 4; i <= n; i++) {
            for(int j = 1; j <= i/2; j++) {
                dp[i] = Math.max(dp[i], dp[j]*dp[i-j]);
            }
        }
        return dp[n];
    }
}

---

解法2：规律

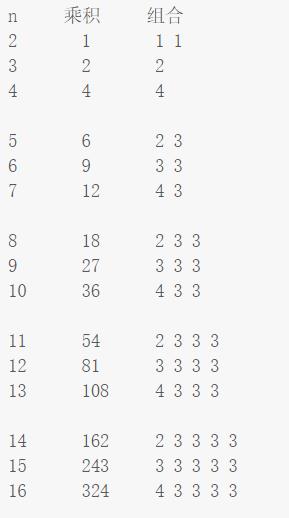
classSolution2 {
    public int cuttingRope(int n) {
        if(n < 4) return n-1;
        int sum = 1;
        while(n > 4) { sum*=3; n-=3; }
        sum *= n;
        return sum;
    }
}