数学建模基于元胞自动机的短消息网络病毒传播仿真
Posted MatlabQQ1575304183
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学建模基于元胞自动机的短消息网络病毒传播仿真相关的知识,希望对你有一定的参考价值。
元胞自动机的初步理解
- 对元胞自动机的初步认识
元胞自动机(CA)是一种用来仿真局部规则和局部联系的方法。典型的元
胞自动机是定义在网格上的,每一个点上的网格代表一个元胞与一种有限的状
态。变化规则适用于每一个元胞并且同时进行。 - 元胞的变化规则&元胞状态
典型的变化规则,决定于元胞的状态,以及其( 4 或 8 )邻居的状态。 - 元胞自动机的应用
元胞自动机已被应用于物理模拟,生物模拟等领域。 - 元胞自动机的matlab编程
结合以上,我们可以理解元胞自动机仿真需要理解三点。一是元胞,在matlab中可以理解为矩阵中的一点或多点组成的方形块,一般我们用矩阵中的一点代表一个元胞。二是变化规则,元胞的变化规则决定元胞下一刻的状态。三是元胞的状态,元胞的状态是自定义的,通常是对立的状态,比如生物的存活状态或死亡状态,红灯或绿灯,该点有障碍物或者没有障碍物等等。
function Message_Spread_Modeticload 'Data\\Link.txt'; %读入连接矩阵% load '\\Data\\Point_X.txt'; %读入横坐标% load '\\Data\\Point_Y.txt'; %读入纵坐标%-------------------------------------------------------------------------%%状态分布及状态转移概率SEIR%0:易感状态S(Susceptible) P_0_1; (P_0_3:预免疫系数)%1:潜伏状态E(Exposed) P_1_0;P_1_2;P_1_3%2:染病状态I(Infected) P_2_0;P_2_3%3:免疫状态R(Recovered) P_3_0%-------------------------------------------------------------------------%%计算各用户节点的度De=sum(Link); %用户节点的度%------------——————----参数设置与说明--------------------------------%[M N]=size(Link); %连接矩阵的规模I_E=0.6; %潜伏期E用户的传染强度I_I=0.9; %发病期I用户的传染强度lamda=sum(De)/M; %用户单位时间内平均发送信息的数量%P_m1:用户预免疫系数%State:用户所处状态State=zeros(1,M);0:表示易感状态(Susceptible)%---------------------------------1---------------------------------------%%先讨论用户预免疫系数P_m1对病毒传播的影响TimeStep=50;%input('短信网络内病毒传播模拟时间:');P_m1=[0.1,0.5,0.9]; %用户预免疫系数% State=zeros(TimeStep,M); %用户的状态G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率F_t=5; %F_t:用户从发现病毒到杀毒并升级病毒库的时间for i=1:length(P_m1)TimeLong_F=zeros(1,M); %用户处于染病期的时间长短TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短Sta=zeros(1,M); %用户的状态%进行预免疫设定for j=1:Mif rand(1)<=P_m1(i)Sta(j)=3; %进入免疫状态TimeLong_E(j)=1; %出入潜伏期的时间为1elsecontinue;endend%状态转换%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)%问题:节点度大小存在差别,可能模拟出来的结果有出于% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去[Number,Sta]=Select_Infected_Point(M,Sta,De);%Number:病源节点%State :确定病源节点以后的节点状态矩阵State=zeros(TimeStep,M);Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量for t=1:TimeStepif t==1State(t,:)=Sta;else%模拟每个用户节点的状态for j=1:M%判断用户节点处于什么状态,然后根据其状态确定其转变情况if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移Num=Select_Number_Near(j,Link); %找出节点j的邻居节点P=zeros(1,length(Num)); %邻居节点感染该节点的概率for k=1:length(Num)if State(t-1,Num(k))==1 %节点处于潜伏期E(1)P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...(factorial([1:De(Num(k))]-1)));elseif State(t-1,Num(k))==2 %节点处于染病期I(2)P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./(factorial([1:De(Num(k))]-1)));elsecontinue;endendendP_0_1=max(P); %节点感染病毒的概率if rand<=P_0_1 %此时节点进入潜伏期State(t,j)=1;elseState(t,j)=State(t-1,j);endelseif State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移if rand<=1/(1+exp(-De(j))) %向染病状态I转移State(t,j)=2;TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短elseif rand<=1/(1+exp(-De(j))) %向易感状态S转移State(t,j)=0;elseif rand<=1/(1+exp(-De(j))) %向免疫状态R转移State(t,j)=3;TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1elseState(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)endendendelseif State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移if TimeLong_F(j)<=F_t %表示此时用户不对病毒进行任何处理State(t,j)=State(t-1,j); %此时用户维持在原状态ITimeLong_F(j)=TimeLong_F(j)+2;else%此时用户对进行杀毒并升级病毒库,进入免疫状态RState(t,j)=3;TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度TimeLong_E(j)=1; %进入免疫期的时间长度endelse%此时用户处于免疫期if TimeLong_E<=G_t %病毒此时并未突变,维持原状态R(免疫状态)State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加elseif rand<=1/G_t %病毒突变,状态转移为易感状态SState(t,j)=0;TimeLong_E(j)=0;else%此时用户状态依然不变State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加endendendendendendend%统计各状态的节点数量Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量figure(i)if rem(t,3)==0plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold onplot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold onplot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold onplot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold onelsecontinue;endlegend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')xlabel('模拟时间')ylabel('各状态的用户数量')endendP_m1=0.3; %用户预免疫系数% State=zeros(TimeStep,M); %用户的状态% G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率G_t=[1,5,9];F_t=5; %F_t:用户从发现病毒到杀毒并升级病毒库的时间for i=1:length(G_t)TimeLong_F=zeros(1,M); %用户处于染病期的时间长短TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短Sta=zeros(1,M); %用户的状态%进行预免疫设定for j=1:Mif rand(1)<=P_m1Sta(j)=3; %进入免疫状态TimeLong_E(j)=1; %出入潜伏期的时间为1elsecontinue;endend%状态转换%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)%问题:节点度大小存在差别,可能模拟出来的结果有出于% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去[Number,Sta]=Select_Infected_Point(M,Sta,De);%Number:病源节点%State :确定病源节点以后的节点状态矩阵State=zeros(TimeStep,M);Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量for t=1:TimeStepif t==1State(t,:)=Sta;else%模拟每个用户节点的状态for j=1:M%判断用户节点处于什么状态,然后根据其状态确定其转变情况if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移Num=Select_Number_Near(j,Link); %找出节点j的邻居节点P=zeros(1,length(Num)); %邻居节点感染该节点的概率for k=1:length(Num)if State(t-1,Num(k))==1 %节点处于潜伏期E(1)P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...(factorial([1:De(Num(k))]-1)));elseif State(t-1,Num(k))==2 %节点处于染病期I(2)P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...(factorial([1:De(Num(k))]-1)));elsecontinue;endendendP_0_1=max(P); %节点感染病毒的概率if rand<=P_0_1 %此时节点进入潜伏期State(t,j)=1;elseState(t,j)=State(t-1,j);endelseif State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移if rand<=1/(1+exp(-De(j))) %向染病状态I转移State(t,j)=2;TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短elseif rand<=1/(1+exp(-De(j))) %向易感状态S转移State(t,j)=0;elseif rand<=1/(1+exp(-De(j))) %向免疫状态R转移State(t,j)=3;TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1elseState(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)endendendelseif State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移if TimeLong_F(j)<=F_t %表示此时用户不对病毒进行任何处理State(t,j)=State(t-1,j); %此时用户维持在原状态ITimeLong_F(j)=TimeLong_F(j)+2;else%此时用户对进行杀毒并升级病毒库,进入免疫状态RState(t,j)=3;TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度TimeLong_E(j)=1; %进入免疫期的时间长度endelse%此时用户处于免疫期if TimeLong_E<=G_t(i) %病毒此时并未突变,维持原状态R(免疫状态)State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加elseif rand<=1/G_t(i) %病毒突变,状态转移为易感状态SState(t,j)=0;TimeLong_E(j)=0;else%此时用户状态依然不变State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加endendendendendendend%统计各状态的节点数量Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量figure(i+5)if rem(t,3)==0plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold onplot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold onplot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold onplot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold onelsecontinue;endlegend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')xlabel('模拟时间')ylabel('各状态的用户数量')endendP_m1=0.3; %用户预免疫系数% State=zeros(TimeStep,M); %用户的状态% G_t=5; %G_t:用户的免疫持续时间,反映了病毒的变异频率G_t=5;F_t=[1,5,9]; %F_t:用户从发现病毒到杀毒并升级病毒库的时间for i=1:length(F_t)TimeLong_F=zeros(1,M); %用户处于染病期的时间长短TimeLong_E=zeros(1,M); %用户处于潜伏期的时间长短Sta=zeros(1,M); %用户的状态%进行预免疫设定for j=1:Mif rand(1)<=P_m1Sta(j)=3; %进入免疫状态TimeLong_E(j)=1; %出入潜伏期的时间为1else continue;
元胞自动机的初步理解
- 对元胞自动机的初步认识
元胞自动机(CA)是一种用来仿真局部规则和局部联系的方法。典型的元
胞自动机是定义在网格上的,每一个点上的网格代表一个元胞与一种有限的状
态。变化规则适用于每一个元胞并且同时进行。 - 元胞的变化规则&元胞状态
典型的变化规则,决定于元胞的状态,以及其( 4 或 8 )邻居的状态。 - 元胞自动机的应用
元胞自动机已被应用于物理模拟,生物模拟等领域。 - 元胞自动机的matlab编程
结合以上,我们可以理解元胞自动机仿真需要理解三点。一是元胞,在matlab中可以理解为矩阵中的一点或多点组成的方形块,一般我们用矩阵中的一点代表一个元胞。二是变化规则,元胞的变化规则决定元胞下一刻的状态。三是元胞的状态,元胞的状态是自定义的,通常是对立的状态,比如生物的存活状态或死亡状态,红灯或绿灯,该点有障碍物或者没有障碍物等等。
endend%状态转换%初始随机选择一个节点为病源点(此时不能选处于免疫状态的点)%问题:节点度大小存在差别,可能模拟出来的结果有出于% 为避免这个问题,我们取度最大的节点为病源节点,如果已免疫,则选次大的,一次下去[Number,Sta]=Select_Infected_Point(M,Sta,De);%Number:病源节点%State :确定病源节点以后的节点状态矩阵State=zeros(TimeStep,M);Number_State=zeros(4,TimeStep); %用户处于个状态的统计数量for t=1:TimeStepif t==1State(t,:)=Sta;else%模拟每个用户节点的状态for j=1:M%判断用户节点处于什么状态,然后根据其状态确定其转变情况if State(t-1,j)==0 %此时处于易感状态0,可能向潜伏期转移Num=Select_Number_Near(j,Link); %找出节点j的邻居节点P=zeros(1,length(Num)); %邻居节点感染该节点的概率for k=1:length(Num)if State(t-1,Num(k))==1 %节点处于潜伏期E(1)P(k)=I_E/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...(factorial([1:De(Num(k))]-1)));elseif State(t-1,Num(k))==2 %节点处于染病期I(2)P(k)=I_I/De(Num(k))*sum((lamda.^([1:De(Num(k))]).*exp(-lamda))./...(factorial([1:De(Num(k))]-1)));elsecontinue;endendendP_0_1=max(P); %节点感染病毒的概率if rand<=P_0_1 %此时节点进入潜伏期State(t,j)=1;elseState(t,j)=State(t-1,j);endelseif State(t-1,j)==1 %此时处于潜伏状态E,可能向易感S,染病I和免疫R转移if rand<=1/(1+exp(-De(j))) %向染病状态I转移State(t,j)=2;TimeLong_F(j)=TimeLong_F(j)+1; %用户j处于染病状态的时间长短elseif rand<=1/(1+exp(-De(j))) %向易感状态S转移State(t,j)=0;elseif rand<=1/(1+exp(-De(j))) %向免疫状态R转移State(t,j)=3;TimeLong_E(j)=TimeLong_E(j)+1; %免疫时间增加1elseState(t,j)=State(t-1,j); %状态不变,依然为潜伏期E(1)endendendelseif State(t-1,j)==2 %此时处于欺染病状态I,可能向易感S,免疫R转移if TimeLong_F(j)<=F_t(i) %表示此时用户不对病毒进行任何处理State(t,j)=State(t-1,j); %此时用户维持在原状态ITimeLong_F(j)=TimeLong_F(j)+2;else%此时用户对进行杀毒并升级病毒库,进入免疫状态RState(t,j)=3;TimeLong_F(j)=0; %处于感染期(中毒状态)的时间长度TimeLong_E(j)=1; %进入免疫期的时间长度endelse%此时用户处于免疫期if TimeLong_E<=G_t %病毒此时并未突变,维持原状态R(免疫状态)State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加elseif rand<=1/G_t %病毒突变,状态转移为易感状态SState(t,j)=0;TimeLong_E(j)=0;else%此时用户状态依然不变State(t,j)=State(t-1,j);TimeLong_E(j)=TimeLong_E(j)+1; %处于免疫期的时间增加endendendendendendend%统计各状态的节点数量Number_State(1,t)=sum(State(t,:)==0);%处于易感状态S的总节点数量Number_State(2,t)=sum(State(t,:)==1);%处于易感状态E的总节点数量Number_State(3,t)=sum(State(t,:)==2);%处于易感状态I的总节点数量Number_State(4,t)=sum(State(t,:)==3);%处于易感状态R的总节点数量figure(i+10)if rem(t,3)==0plot([t-1 t],[Number_State(1,t-1) Number_State(1,t)],'md-'),hold onplot([t-1 t],[Number_State(2,t-1) Number_State(2,t)],'gh:'),hold onplot([t-1 t],[Number_State(3,t-1) Number_State(3,t)],'bs-.'),hold onplot([t-1 t],[Number_State(4,t-1) Number_State(4,t)],'k.-'),hold onelsecontinue;endlegend('易感状态Susceptible','潜伏状态Exposed','染病状态Infected','免疫状态Recovered')xlabel('模拟时间')ylabel('各状态的人口数量')endendtoc
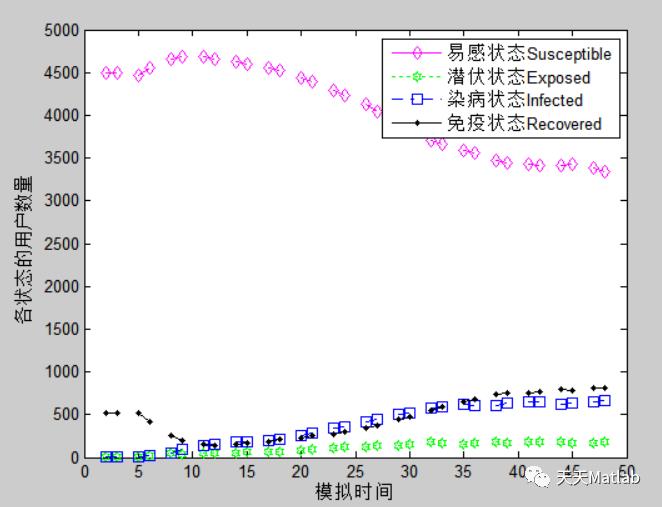
以上是关于数学建模基于元胞自动机的短消息网络病毒传播仿真的主要内容,如果未能解决你的问题,请参考以下文章