Pytorh Note11 Logistic 回归模型

Posted 2021-06-27 Real&Love

Pytorh Note11 Logistic 回归模型

文章目录

• Pytorh Note11 Logistic 回归模型
• • Logistic 回归模型
  • 模型形式
  • Sigmoid 函数
  • 回归问题 vs 分类问题
  • 损失函数
  • Logistic 例子
  • 定义Logistic 回归模型
  • 训练模型 Training
  • 拟合曲线 和 结果展示

全部笔记的汇总贴： Pytorch Note 快乐星球

Logistic 回归模型

机器学习中的监督学习主要分为回归问题和分类问题，我们之前已经讲过回归问题了，它希望预测的结果是连续的，那么分类问题所预测的结果就是离散的类别。这时输入变量可以是离散的，也可以是连续的，而监督学习从数据中学习一个分类模型或者分类决策函数，它被称为分类器（classifier）。分类器对新的输入进行输出预测，这个过程即称为分类（classification）。例如，判断邮件是否为垃圾邮件，医生判断病人是否生病，或者预测明天天气是否下雨等。同时分类问题中包括有二分类和多分类问题，我们下面先讲一下最著名的二分类算法——Logistic 回归。首先从 Logistic 回归的起源说起。

Logistic 起源于对人口数量增长情况的研究，后来又被应用到了对于微生物生长情况的研究，以及解决经济学相关的问题，现在作为回归分析的一个分支来处理分类问题，先从 Logistic 分布入手，再由 Logistic 分布推出 Logistic 回归

模型形式

Logistic 回归的模型形式和线性回归一样，都是 $y=wx+b$，其中 x 可以是一个多维的特征，唯一不同的地方在于 Logistic 回归会对 y 作用一个 logistic 函数，将其变为一种概率的结果。 Logistic 函数作为 Logistic 回归的核心，我们下面讲一讲 Logistic 函数，也被称为 Sigmoid 函数。

Sigmoid 函数

Sigmoid 函数非常简单，其公式如下

$$f(x)=\frac{1}{1+e^{-x}}$$

Sigmoid 函数的图像如下

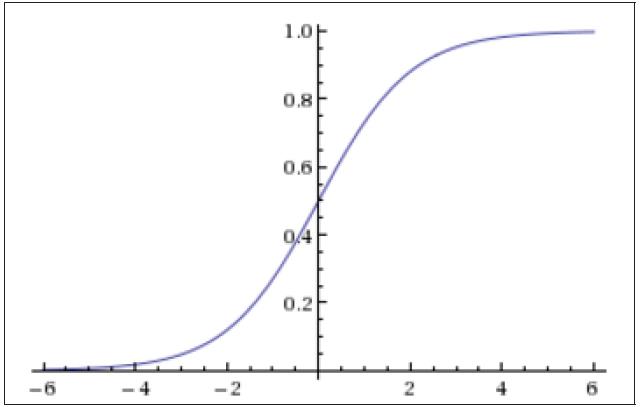
可以看到 Sigmoid 函数的范围是在 0 ~ 1 之间，所以任何一个值经过了 Sigmoid 函数的作用，都会变成 0 ~ 1 之间的一个值，这个值可以形象地理解为一个概率，比如对于二分类问题，这个值越小就表示属于第一类，这个值越大就表示属于第二类。

另外一个 Logistic 回归的前提是确保你的数据具有非常良好的线性可分性，也就是说，你的数据集能够在一定的维度上被分为两个部分，比如

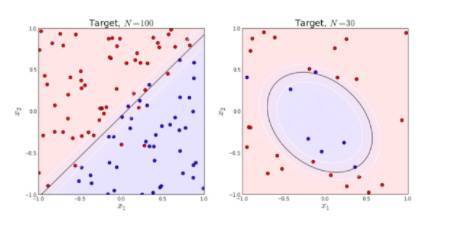
可以看到，上面红色的点和蓝色的点能够几乎被一个平面分割开来

回归问题 vs 分类问题

Logistic 回归处理的是一个分类问题，而上一个模型是回归模型，那么回归问题和分类问题的区别在哪里呢？

从上面的图可以看出，分类问题希望把数据集分到某一类，比如一个 3 分类问题，那么对于任何一个数据点，我们都希望找到其到底属于哪一类，最终的结果只有三种情况，{0, 1, 2}，所以这是一个离散的问题。

而回归问题是一个连续的问题，比如曲线的拟合，我们可以拟合任意的函数结果，这个结果是一个连续的值。

分类问题和回归问题是机器学习和深度学习的第一步，拿到任何一个问题，我们都需要先确定其到底是分类还是回归，然后再进行算法设计

损失函数

前一节对于回归问题，我们有一个 loss 去衡量误差，那么对于分类问题，我们如何去衡量这个误差，并设计 loss 函数呢？

Logistic 回归使用了 Sigmoid 函数将结果变到 0 ~ 1 之间，对于任意输入一个数据，经过 Sigmoid 之后的结果我们记为 $\hat{y}$，表示这个数据点属于第二类的概率，那么其属于第一类的概率就是 $1-\hat{y}$。如果这个数据点属于第二类，我们希望 $\hat{y}$ 越大越好，也就是越靠近 1 越好，如果这个数据属于第一类，那么我们希望 $1-\hat{y}$ 越大越好，也就是 $\hat{y}$ 越小越好，越靠近 0 越好，所以我们可以这样设计我们的 loss 函数

$$loss=-(y\ast log(\hat{y})+(1-y)\ast log(1-\hat{y}))$$

其中 y 表示真实的 label，只能取 {0, 1} 这两个值，因为 $\hat{y}$ 表示经过 Logistic 回归预测之后的结果，是一个 0 ~ 1 之间的小数。如果 y 是 0，表示该数据属于第一类，我们希望 $\hat{y}$ 越小越好，上面的 loss 函数变为

$$loss=-(log(1-\hat{y}))$$

在训练模型的时候我们希望最小化 loss 函数，根据 log 函数的单调性，也就是最小化 $\hat{y}$，与我们的要求是一致的。

而如果 y 是 1，表示该数据属于第二类，我们希望 $\hat{y}$ 越大越好，同时上面的 loss 函数变为

$$loss=-(log(\hat{y}))$$

我们希望最小化 loss 函数也就是最大化 $\hat{y}$，这也与我们的要求一致。

所以通过上面的论述，说明了这么构建 loss 函数是合理的。

Logistic 例子

import torch
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

我们从 data.txt 读入数据，感兴趣的同学可以打开 data.txt 文件进行查看

读入数据点之后我们根据不同的 label 将数据点分为了红色和蓝色，并且画图展示出来了

# 从 data.txt 中读入点
with open('./data.txt', 'r') as f:
    data_list = [i.split('\\n')[0].split(',') for i in f.readlines()]
    data = [(float(i[0]), float(i[1]), float(i[2])) for i in data_list]

# 标准化
x0_max = max([i[0] for i in data])
x1_max = max([i[1] for i in data])
data = [(i[0]/x0_max, i[1]/x1_max, i[2]) for i in data]

x0 = list(filter(lambda x: x[-1] == 0.0, data)) # 选择第一类的点
x1 = list(filter(lambda x: x[-1] == 1.0, data)) # 选择第二类的点

plot_x0 = [i[0] for i in x0]
plot_y0 = [i[1] for i in x0]
plot_x1 = [i[0] for i in x1]
plot_y1 = [i[1] for i in x1]

plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')

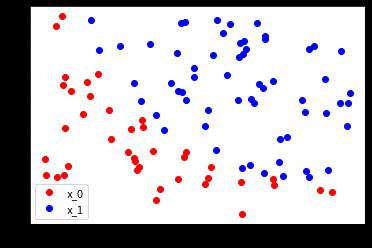
定义Logistic 回归模型

class  LogisticRegression(nn.Module):
	def  __init__(self):
		super(LogisticRegression,  self).__init__()
		self.lr  =  nn.Linear(2,  1)
		self.sm  =  nn.Sigmoid()


	def  forward(self,  x):
		x  =  self.lr(x)
		x  =  self.sm(x)
		return  x

logistic_model  =  LogisticRegression()
if  torch.cuda.is_available():
	logistic_model.cuda()

criterion  =  nn.BCELoss()
optimizer  =  torch.optim.SGD(logistic_model.parameters(),  lr=1e-3,
momentum=0.9)

这里 nn.BCELoss 是二分类的损失函数，torch.optim.SGD 是随机梯度下降优化函数。然后训练模型，并且间隔一定的迭代次数输出结果。

训练模型 Training

for  epoch  in  range(50000):
	if  torch.cuda.is_available():
		x  =  Variable(x_data).cuda()
		y  =  Variable(y_data).cuda()
	else:
		x  =  Variable(x_data)
		y  =  Variable(y_data)
    #  ==================forward==================
    out  =  logistic_model(x)
    loss  =  criterion(out,  y)
    print_loss  =  loss.data
    mask  =  out.ge(0.5).float()
    correct  =  (mask  ==  y).sum()
    acc  =  correct.data[0]  /  x.size(0)
    #  ===================backward=================
    optimizer.zero_grad()

    loss.backward()
    optimizer.step()
	if  (epoch+1)  %  1000  ==  0:
        print('*'*10)
        print('epoch  {}'.format(epoch+1))
        print('loss  is  {:.4f}'.format(print_loss))
        print('acc  is  {:.4f}'.format(acc))

其中 mask=out.ge(0.5).float() 是判断输出结果如果大于 0.5 就等于 1，小于0.5 就等于 0，通过这个来计算模型分类的准确率。

因为数据相对简单，同时我们使用的是也是简单的线性 Logistic 回归，loss 已经降得相对较低，同时也有 91% 的准确率。

epoch  46000
loss  is  0.3116
acc  is  0.9100
**********
epoch  47000
loss  is  0.3098
acc  is  0.9100
**********
epoch  48000
loss  is  0.3080
acc  is  0.9100
**********
epoch  49000
loss  is  0.3063
acc  is  0.9100
**********
epoch  50000
loss  is  0.3046
acc  is  0.9100

拟合曲线 和 结果展示

w0,  w1  =  logistic_model.lr.weight[0]
w0  =  w0.data.cpu()
w1  =  w1.data.cpu()
b  =  logistic_model.lr.bias.data[0].cpu()
plot_x  =  np.arange(0.2,  1,  0.1)


plot_y  =  (-w0  *  plot_x  -  b)  /  w1
plt.plot(plot_x, plot_y, 'g', label='cutting line')
plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')

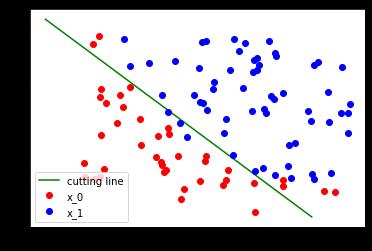
以上我们介绍了分类问题中的二分类问题和 Logistic 回归算法，一般来说，Logistic回归也可以处理多分类问题，但最常见的还是应用在处理二分类问题上，下一节会讲一下如何用神经网络解决非线性的分类问题

下一章传送门：Note12 多层神经网络