最小生成树之普里姆，克鲁斯卡尔(c)

Posted 2021-06-27 田啊田

最小生成树

图是由顶点和顶点之间边的集合组成的，它的顶点是有穷的，而有些图顶点之间的边可以用来表示两点之间的距离或者耗费(权值)的图称为网。

如果要让你把带权的图，即网结构连接起来，这时候方法就有好多种了，就像在电子电路的设计中，我们会将每一个针脚连接起来，并且让其的代价最小，这时候，电路就像一个网。，但是再加上要求(最短的距离)那我们该怎么做？由于最短距离是无环的，并且连通所有的顶点，因此它一定是棵树。

在图中，将上面的问题用连通无向图G(V,E)来表示，其中V表示图中的顶点集合，E表示图中的可能连接，对于每条边都有(u，v)∈E,(u，v∈V），如果w(u,v)是连接顶点的代价，那我们是找连接无环子集T∈E，将图中的所有点都连接起来，并且使子集的代价最小，即∑(u,v)的值最小，这时候连接的无环图就是最小生成树。

连通无向图G(V,E)

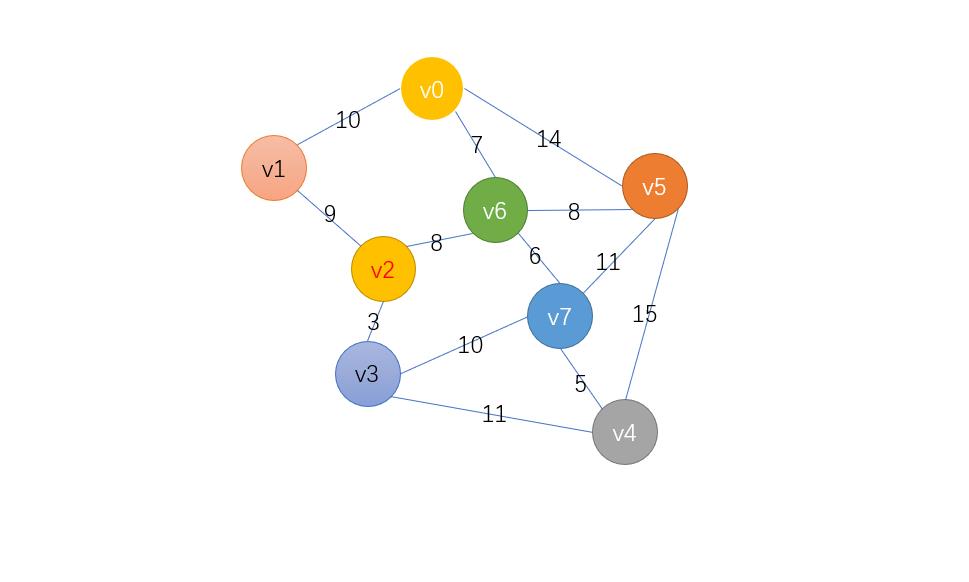
找网的最小生成树，最经典的有两种算法，普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法，下面我们就将这两种算法简单介绍一下。

一． 普里姆(Prim)算法

建立上图的邻接矩阵如下图所示。

它的思维是这样的，从某一顶点出发，遍历周围的点找出最小的路径，不二次遍历且遍历完所有的顶点。

算法思维：首先建立两个数组，一个用来保存相关顶点的下标a数组，另一个用来保存相关顶点间边的权值b数组。a数组的大小为MAX(MAX是顶点个数最大值，该矩阵中大于等于8即可)，初始值为0，b数组的大小为MAX，初始值为INFINITY 65535(数组中用65535代替∞)。普里姆算法最核心的地方就是这两个数组。

它把与V0连接的顶点的边的权值输入到b数组，循环全部的顶点，在条件为b数组中该位置的值不为0且小于最小值得时候用该值代替最小值。输出打印。在这里有一个巧妙的设计，该值不为0，这样我们把已经用过的值就可以设置为0，而不在下次使用了。然后循环所有的顶点找到与第一个值和刚才找的最小的值相连接的顶点，从与它们相连接的顶点中继续找下一个距离最小的权值。

看一下代码是怎么实现的。

typedef struct
{
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int a[MAXVEX];	
	int b[MAXVEX];	
	b[0] = 0;
	a[0] = 0;			
	for(i = 1; i < G.numVertexes; i++)	
	{
		b[i] = G.arc[0][i];	
		a[i] = 0;					
	}
	for(i = 1; i < G.numVertexes; i++)
	{
		min = INFINITY;	
		j = 1;k = 0;
		while(j < G.numVertexes)	
		{
			if(b[j]!=0 && b[j] < min)
			{	
				min = b[j];	
				k = j;			
			}
			j++;
		}
		printf("(%d, %d)\\n", a[k], k);
		b[k] = 0;
		for(j = 1; j < G.numVertexes; j++)	
		{
			if(b[j]!=0 && G.arc[k][j] < b[j]) 
			{
				b[j] = G.arc[k][j];
				a[j] = k;				
			}
		}
	}
}

在存入与V0顶点与之有边的权值前，要给a，b数组的第V0项赋值为0。时间复杂度为O(n^2)

二． 克鲁斯卡尔(Kruskal)算法

该网构成的边集数组如下所示。

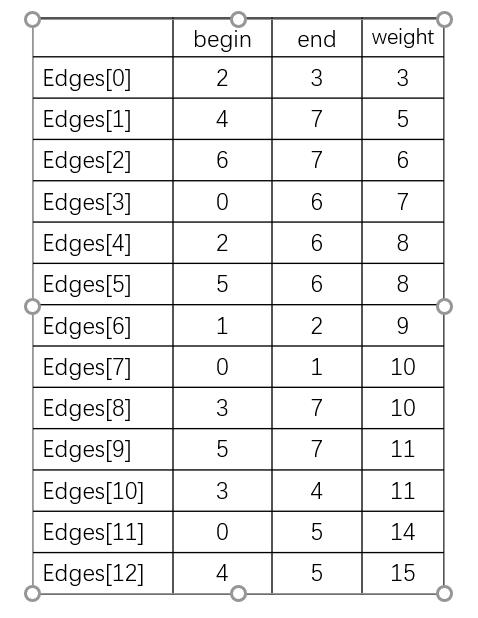
克鲁斯卡尔算法是直接以边去构建的，构建时我们只需要考虑是否构成环路。

它的思维是这样的，将所有最小的权值连接起来，只要它不构成回路并且遍历完了每一个顶点。

算法思维：定义一数组a[max]用来判断边与边是否构成了回路，max是顶点数的最大个数。初始化a数组值全为0，在遍历某个点后，把end的值赋给a[begin]里面，如果a[begin]的值不为0，则把end的值赋给a[a[begin]]里面如果a[a[begin]]的值仍不为0，则继续赋给a[a[a[begin]]]里面，依次类推，且如果有这两个值相等，则就说明构成了回路。是不是像思维也转了个圈。

typedef struct
{
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

void MiniSpanTree_Kruskal(MGraph G)
{
	int i, j, n, m;
	int k = 0;
	int a[MAXVEX];
	Edge edges[MAXEDGE];
	for (i = 0; i < G.numVertexes; i++)
		a[i] = 0;	
	printf("打印最小生成树：\\n");
	for (i = 0; i < G.numEdges; i++)	
	{
		n = Find(a,edges[i].begin);
		m = Find(a,edges[i].end);
		if (n != m) 
		{
			a[n] = m;	
			printf("(%d, %d) %d\\n", edges[i].begin, edges[i].end, edges[i].weight);
		}
	}
}
int Find(int *a, int f)
{
	while ( a[f] > 0)
	{
		f = a[f];
	}
	return f;
}

克鲁斯卡尔算法的时间表示为O(ElgV)

优化普里姆算法的时间复杂度。