0-1背包问题

Posted 2021-06-27 超浪*牛

动态规划之0~1背包笔记：

问题描述：

有n个物品有各自的体积和价值，现在给容量的背包， 如何让背包里装入的物品具有最大的价值总和

最优性原理：不论初始状态如何和初始决策如何，对于前面的决策所造成的某一状态而言，其后各阶段的决策序列必须构成最优策略。

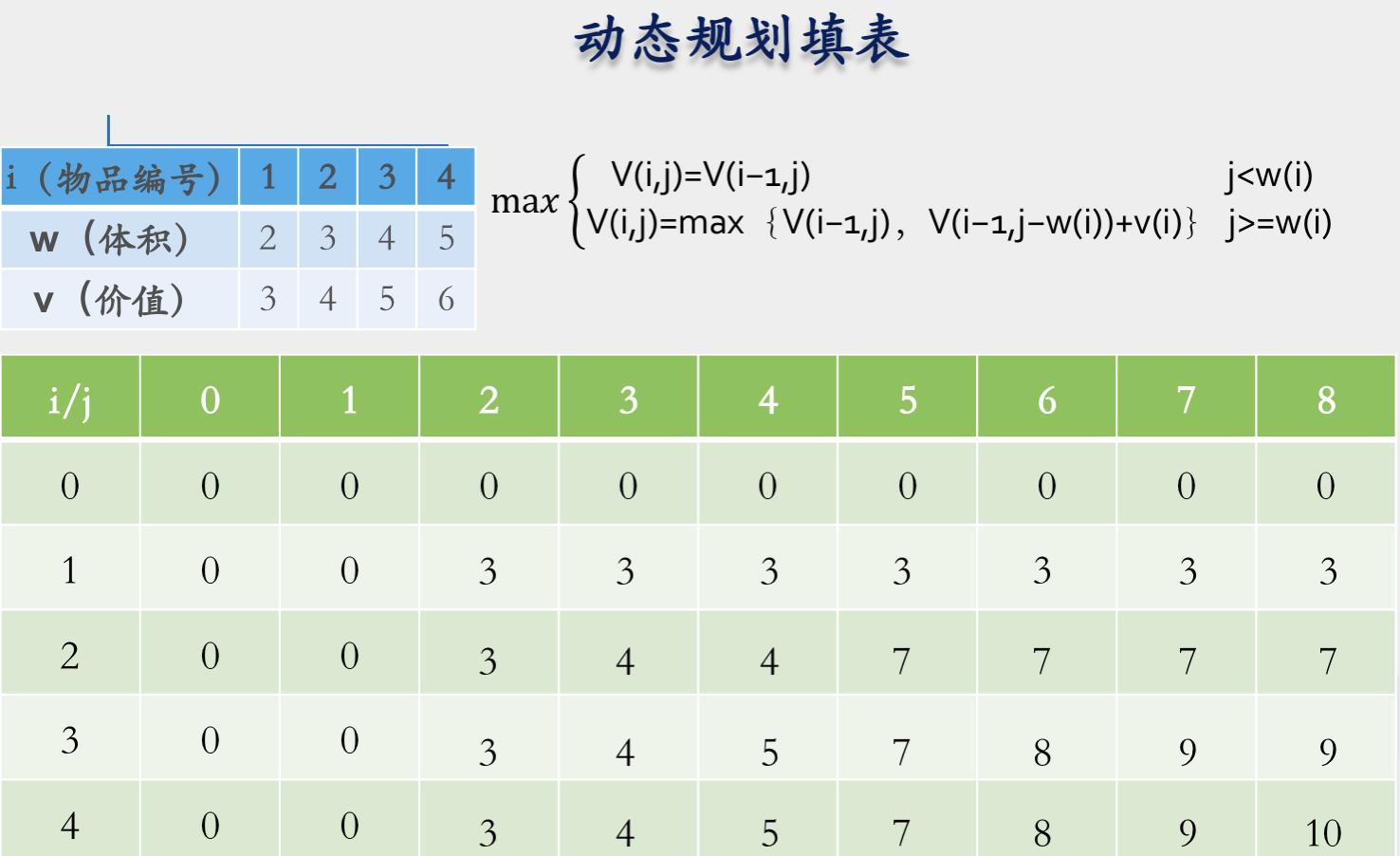
代码描述

/***********************************************************
*版权所有：(C) 2021.6.12 烽火大队-狼烟一号（第八方面军） 
* 
*文件名称： 0-1背包问题 
*内容摘要：	有n个物品有各自的体积和价值，现在给容量的背包。 
			如何让背包里装入的物品具有 最大的价值总和 
*当前版本： 1-1 
*文件作者：牛鹏 
*完成日期：2021.6.12
*备注	 ：动态规划法 
*修改记录：暂无 
***********************************************************/
#include <stdio.h>
#include <stdlib.h>
int max(int a,int b);//返回较大的那个数字 
int main() {
	int w[5] = {0,2,3,4,5};		/*商品的体积为2,3,4,5*/
	int v[5] = {0,3,4,5,6};		/*商品的价值是3,4,5,6*/
	int bagV = 8;//包的容量
	int dp[5][9] = {{0}}; 		/*动态规划表（表的大小手动模拟可知）*/
	int i=0,j=0;
	for(i=1;i<=4;i++){
		for(j=1;j<=bagV;j++){
			if(j<w[i]){
				dp[i][j] = dp[i-1][j];
			}else{
				dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
			}
		}
	}
	printf("最大价值是：%d",dp[4][8]); 
	return 0;
}
int max(int a,int b){
	if(a>=b){
		return a;
	}else{
		return b;
	}
}