严格上升子序列数（树状数组）（离散化优化）

Posted 2021-06-27 SSL_LKJ

严格上升子序列数

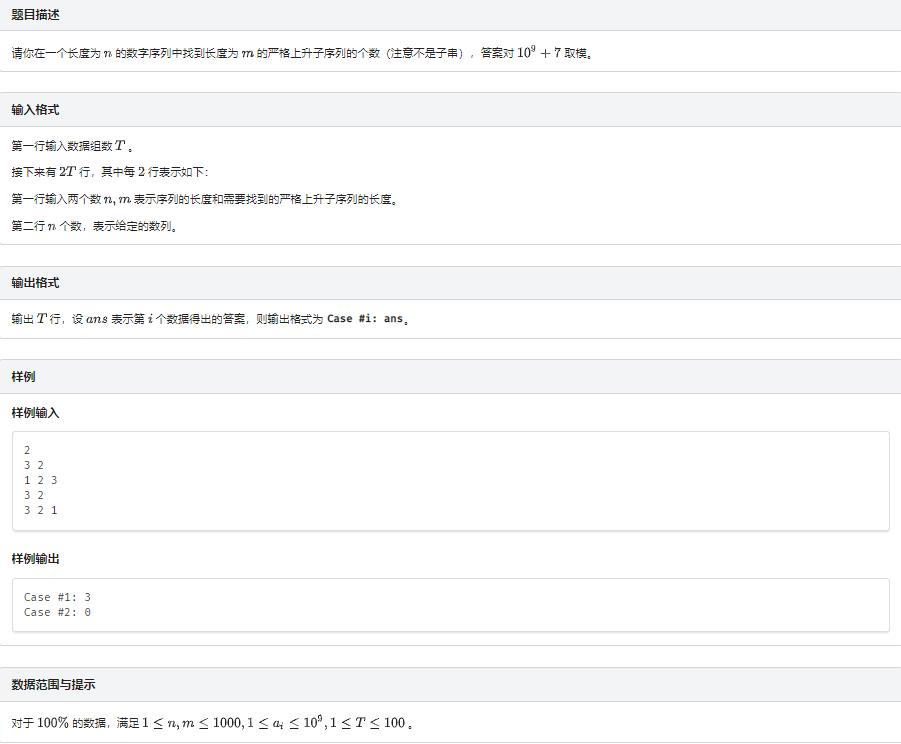
解题思路

这题跟P1908 逆序对（树状数组）（离散化优化）有异曲同工之妙
可推出式子

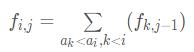
（设f(i,j)表示以第i个数结尾、长度为j的严格上升子序列数）
当然
当j=1时结果为1
再用离散化优化

AC代码

#include<algorithm>
#include<cstring>
#include<cstdio>
long long n,m,a[1005],b[1005],c[1005][1005],f[1005][1005];
using namespace std;
long long lowbit(long long x)
{
	return x&(-x); 
}
void update(long long x,long long i,long long y)//存储
{
	for(;i<=n;i+=lowbit(i))c[x][i]+=y;
}
long long query(long long x,long long i)//查询
{
	long long sum=0;
	for(;i;i-=lowbit(i))sum+=c[x][i];
	return sum;
}
int main()
{
	long long T,t=0;
	scanf("%lld",&T);
	while(T--)
	{
		long long ans=0;
		memset(f,0,sizeof(f));
		memset(c,0,sizeof(c));
		t++;
		scanf("%lld%lld",&n,&m);
		for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
    	for(long long i=1;i<=n;i++)b[i]=a[i];//离散化
    	sort(b+1,b+n+1);
    	long long tot=unique(b+1,b+1+n)-1-b;
    	for(long long i=1;i<=n;i++)
     	 a[i]=lower_bound(b+1,b+1+tot,a[i])-b;
     	for(long long i=1;i<=n;i++)//dp
     	 for(long long j=1;j<=m;j++)
		 {
		 	if(j==1)f[i][j]=1;
		 	else f[i][j]=query(j-1,a[i]-1);
		 	update(j,a[i],f[i][j]);
		 }
		for(long long i=m;i<=n;i++)ans+=f[i][m];
		printf("Case #%lld: %lld\\n",t,ans);
	}
}

谢谢