特化的AVL树之红黑树学习及原理解析

Posted 2021-06-27 踩踩踩从踩

二叉平衡搜索树AVL 学习解析 及代码实现研究

前言

之前我分析过avl树，今天我在继续分析特化的AVL树（红黑树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。在我们实际的用途中，用的很多；例如 TreeMap排序等等，以达到快速查找数据的效果

性质和定义

红黑树（RBT）的定义：它或者是一棵空树，或者是具有一下性质的平衡二叉查找树   

• 节点非红即黑。
• 根节点是黑色
• 所有null结点称为叶子节点，且认为颜色为黑色
• 所有红节点的子节点都为黑色
• 从任意节点到其叶子节点 的所有路径上都包含相同数目的黑节点。

上图根据红黑树的基本性质，做了一个基本的红黑树展示

性质

对平衡树的一种改进，任意一个节点，它的红黑树的间隔不超过一倍，但它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。 

• 红黑树需要维持颜色变更，因此 插入和删除保持为 O（log n)）次；
• avl树需要维持任何节点的两个子树最大差别为1；因此总的来说，建树复杂度为O(NlogN)
• 红黑树是二叉排序树，因此可以采用中序遍历法，进行遍历出排序好的数据
•  在树的删除增加节点时，为保持

从插入节点进行分析

插入节点

• 先按照二叉排序树 的方式插入节点 设置为红色    我们分析过二叉排序树如何插入节点 ；

二叉排序树学习构建方式及如何遍历二叉排序树

  插入节点过后就有可能导致用红黑树颜色不正确，因此我们需要重新维持树型

• 插入的是根节点，直接将  节点红色涂黑

• 插入的节点的父节点是黑色，不违背任何性质，不用调整

插入节点的父节点是红色 ，就有下面几种情况

• 父节点是祖父节点的左孩子    祖父节点的另一个子节点（叔叔节点）是红色    (node.parent=node.parent.parent.leftchild   node.parent.parent.right=read)

      对策： 将当前节点的父节点和叔叔节点涂黑，祖父节点涂红，把当前节点指向祖父节点，从新的当前节点开始算法

 n节点代表 当前节点  p 代表父亲节点  g 代表祖父节点  u代表叔叔节点

     为什么这样去把原有节点的父亲节点涂，这也是为了保证红黑树的特性不变因此做的处理，需要将祖父节点涂红 

• 插入节点的父节点是红色 ，父节点是祖父节点的左孩子；叔叔节点是黑色，当前节点是其父节点的右孩子

对策： 当前节点的父节点做为新的当前节点，以新当前节点为支点左旋。

 

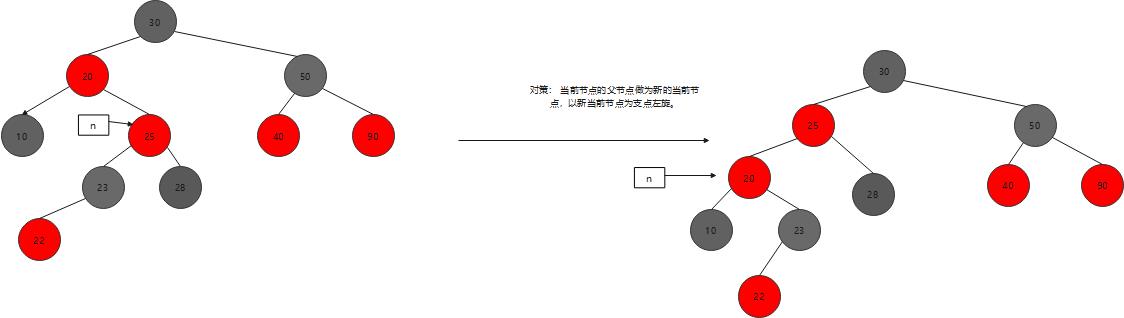
• 插入节点的父节点是红色 ，父节点是祖父节点的左孩子；叔叔节点是黑色，当前节点是其父节点的左孩子

     对策：父节点变为黑色，祖父节点变红色，再祖父节点为支点进行右旋

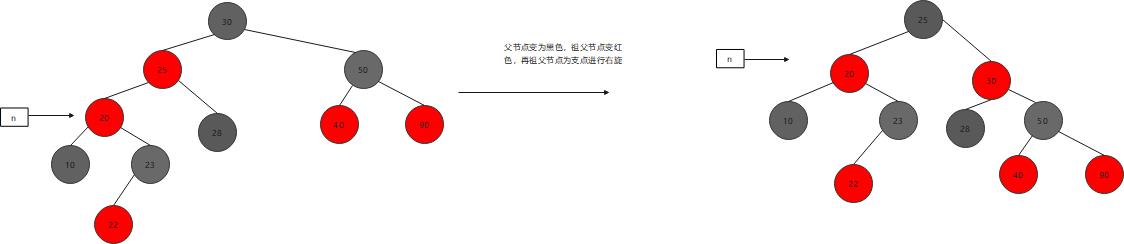
父节点是祖父节点的右孩子，和上面情况一样，将左全部变成右即可

 

删除节点

删除节点：先进行二叉排序树的删除操作，然后已替换节点作为当前节点进行后面的平衡操作  

• 当前节点是红色，直接把当前节点染成黑色，结束。
• 当前节点x是黑色 ，被删除节点是父节点的左孩子，当前节点是根节点 保持原样
• 当前节点x是黑色，被删除节点是父节点的左孩子，当前节点x的兄弟节点是红色(此时父节点和兄弟节点的子节点分为黑)

     对策：把父节点染成红色，兄弟节点染成黑色，对父节点进行左旋，重新设置x的兄弟节点

• 当前节点x 的兄弟节点是黑色 ，被删除节点是父节点的左孩子，兄弟节点的两个孩子都是黑色 

     对策：将x的兄弟节点设为红色，设置x的父节点为新的x节点

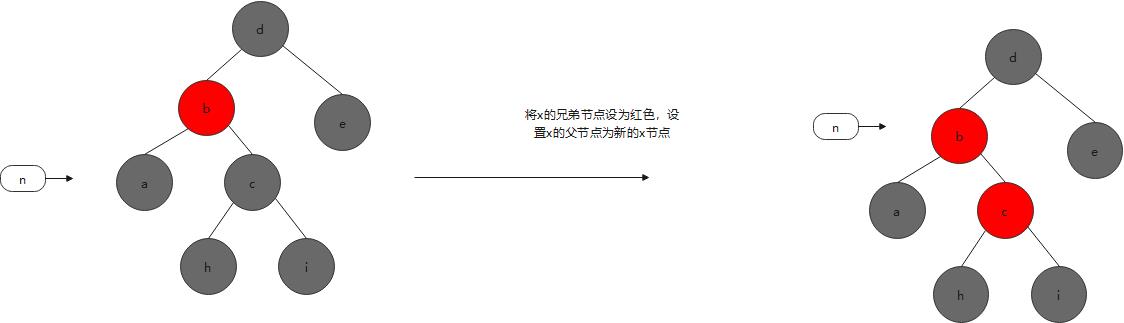
• 当前节点x 的兄弟节点是黑色 被删除节点是父节点的左孩子，兄弟的右孩子是黑色，左孩子是红色

   对策：将x兄弟节点的左孩子设为黑色，将x兄弟节点设置红色，将x的兄弟节点右旋，右旋后，重新设置x的兄弟节点。

• 当前节点x 的兄弟节点是黑色 被删除节点是父节点的左孩子，兄弟节点的右孩子是红色

对策：把兄弟节点染成当前节点父节点颜色，把当前节点父节点染成黑色，兄弟节点右孩子染成黑色，再以当前节点的父节点为支点进行左旋，算法结算

 

被删除节点是父节点的右孩子 把上面的左设置为右

 

 总结

整个红黑树的原理，保证二叉排序树；其次主要就是围绕着保证红黑树特性，保证它的特性；降低查询数据的时间复杂度，在代码中还是应用很多的；这篇数据结构我没有代码的实现分析，我放到了treemap里面分析；大家有兴趣可以关注我分析的treemap集合