以MATLAB的方式实现微积分问题的计算机求解问题及解决方案集锦
Posted 文宇肃然
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了以MATLAB的方式实现微积分问题的计算机求解问题及解决方案集锦相关的知识,希望对你有一定的参考价值。
前言
关于MATLAB系列的精品专栏大家可参见
喜欢的小伙伴可自行订阅,你的支持就是我不断更新的动力哟!
微积分问题的计算机求解系列 (0001)
试求出下面的定积分或无穷积分。
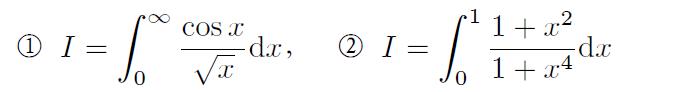
【解】
① 可以直接求解
>> syms x; int(cos(x)/sqrt(x),x,0,inf)
ans =
1/2*2^(1/2)*pi^(1/2)
② 可以得出
>> syms x; int((1+x^2)/(1+x^4),x,0,1)
ans =
1/4*2^(1/2)*pi
拓展1:
假设
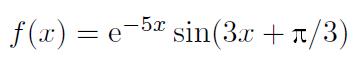
试求出积分函数
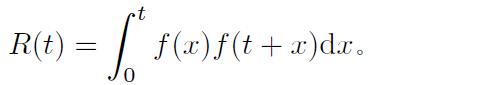
【解】
定义了 x 的函数,则可以由 subs() 函数定义出 t + x 的函数,这样由下面的语句可以直接得出 R 函数。
>> syms x t;
f=exp(-5*x)*sin(3*x+sym(pi)/3);
R=int(f*subs(f,x,t+x),x,0,t);
simple(R)
ans =
1/1360*(15*exp(t)^10*3^(1/2)*cos(3*t)-25*cos(9*t)+
25*exp(t)^10*3^(1/2)*sin(3*t)-68*cos(3*t)-15*3^(1/2)*cos(9*t)-
25*3^(1/2)*sin(9*t)-15*exp(t)^10*sin(3*t)+15*sin(9*t)+ 93*exp(t)^10*cos(3*t))/exp(t)^15
该结果可以写成
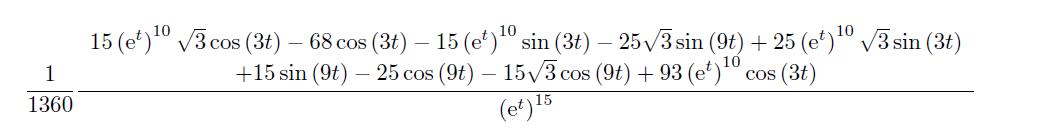
拓展2:
对 a 的不同取值,试求出
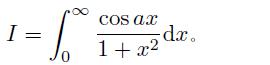
【解】
由下面的循环结构可以得出不同 a 值下的无穷积分值,并可以绘制出它们之间关系的曲线,如图所示。
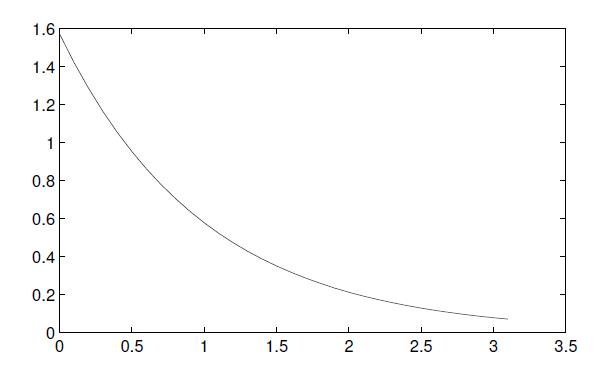
>> syms x a;
f=cos(a*x)/(1+x^2);
aa=[0:0.1:pi];
y=[];
for n=aa
b=int(subs(f,a,n),x,0,inf);
y=[y, double(b)];
end
plot(aa,y)
微积分问题的计算机求解系列 (0002)
问题:
试对下面函数进行 Fourier 幂级数展开。
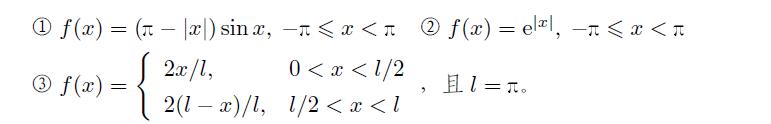
【解】
① 可以立即由下面的语句求出。
>> syms x;
f=(sym(pi)-abs(x))*sin(x);
[A,B,F]=fseries(f,x,10,-pi,pi);
F
F =
1/2*pi*sin(x)+16/9/pi*sin(2*x)+32/225/pi*sin(4*x)+ 48/1225/pi*sin(6*x)+64/3969/pi*sin(8*x)+80/9801/pi*sin(10*x)
该结果在 LATEX 下可以显示为:
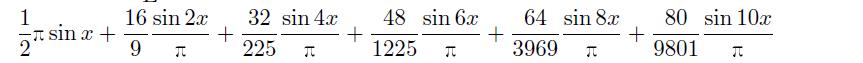
② 可以由下面语句求解,并得出数学公式为
>> syms x;
f=exp(abs(x));
[A,B,F]=fseries(f,x,10,-pi,pi);
F
得出的解析解为
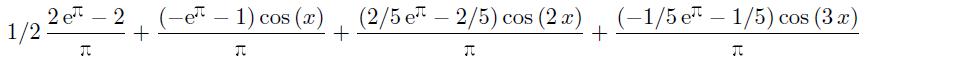
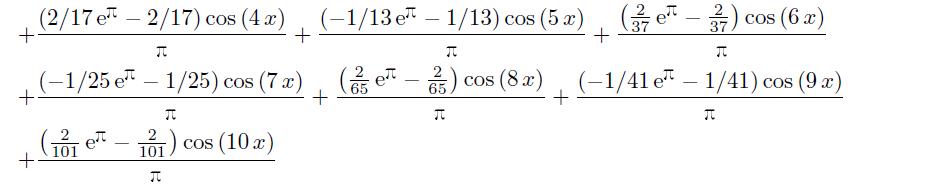
进一步观察结果可见,该式子可以手工化简。
例如,提取系数
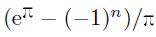
或对各项系数逐项求值 (保留 10 位有效数字)
>> vpa(F,10)
ans =
7.047601355-7.684221126*cos(x)+2.819040541*cos(2.*x)-1.536844225*cos(3.*x)
+.8291295709*cos(4.*x)-.5910939328*cos(5.*x)+.3809514246*cos(6.*x)
-.3073688450*cos(7.*x)+.2168492724*cos(8.*x)-.1874200274*cos(9.*x)
+.1395564625*cos(10.*x)
③ 似乎求解起来更困难,巧妙利用符号运算工具箱中的 heaviside() 函数,则可以将原函数 表示成
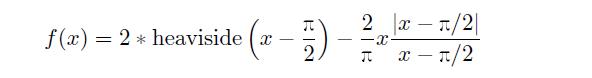
这样就可以用下面的语句求出函数的 Fourier 级数。
>> syms x;
pi1=sym(pi);
f=2*heaviside(x-pi1/2)-2/pi1*x*abs(x-pi1/2)/(x-pi1/2); [a,b,F]=fseries(f,x,10,-pi,pi);
F
F =
-1/4+4/pi^2*cos(x)+(4/pi+2)/pi*sin(x)-2/pi^2*cos(2*x)-1/pi*sin(2*x)+ 4/9/pi^2*cos(3*x)+(-4/9/pi+2/3)/pi*sin(3*x)-1/2/pi*sin(4*x)+ 4/25/pi^2*cos(5*x)+(4/25/pi+2/5)/pi*sin(5*x)-2/9/pi^2*cos(6*x)- 1/3/pi*sin(6*x)+4/49/pi^2*cos(7*x)+(-4/49/pi+2/7)/pi*sin(7*x)- 1/4/pi*sin(8*x)+4/81/pi^2*cos(9*x)+(4/81/pi+2/9)/pi*sin(9*x)- 2/25/pi^2*cos(10*x)-1/5/pi*sin(10*x)
该结果在 LATEX 下可以显示为
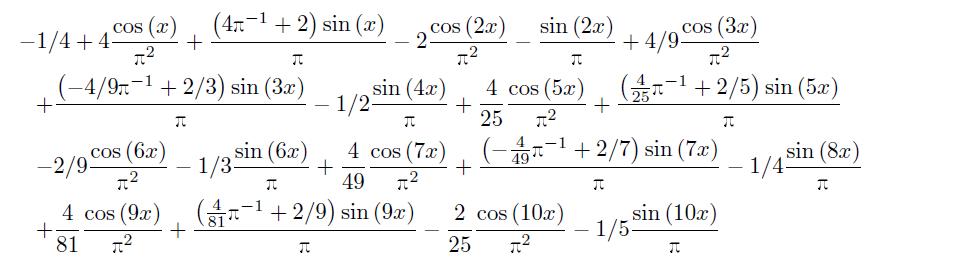
拓展1:
试求出下面函数的 Taylor 幂级数展开。
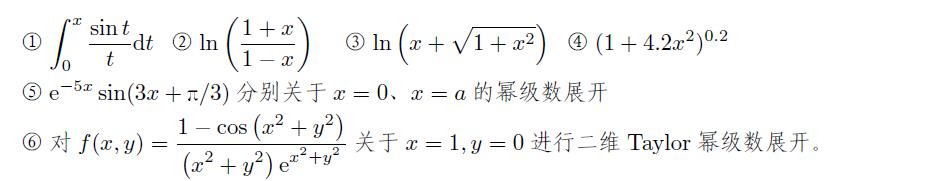
【解】 由下面的语句可以分别求出各个函数的幂级数展开,
>> syms t x; f=int(sin(t)/t,t,0,x); taylor(f,x,15)
>> syms x; f=log((1+x)/(1-x)), taylor(f,x,15)
>> syms x; f=log(x+sqrt(1+x^2)); taylor(f,x,15)
>> syms x; f=(1+4.2*x^2)^0.2; taylor(f,x,13)
由 latex(ans) 函数可以得出下面的数学表示形式。
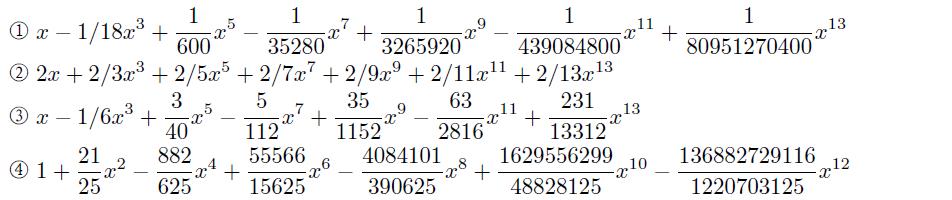
⑤ 该函数的前 4 项展开为
>> syms x a; f=exp(-5*x)*sin(3*x+sym(pi)/3); taylor(f,x,4,a)
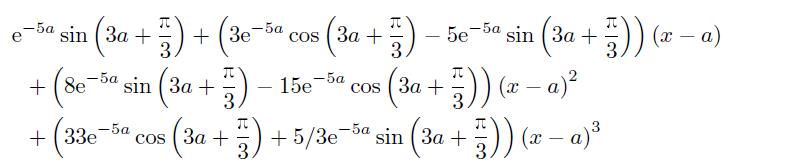
⑥ 该函数需要使用 Maple 的展开函数。
>> syms x y; f=(1-cos(x^2+y^2))/((x^2+y^2)*exp(x^2+y^2)); F=maple(’mtaylor’,f,’[x=1,y]’,4)
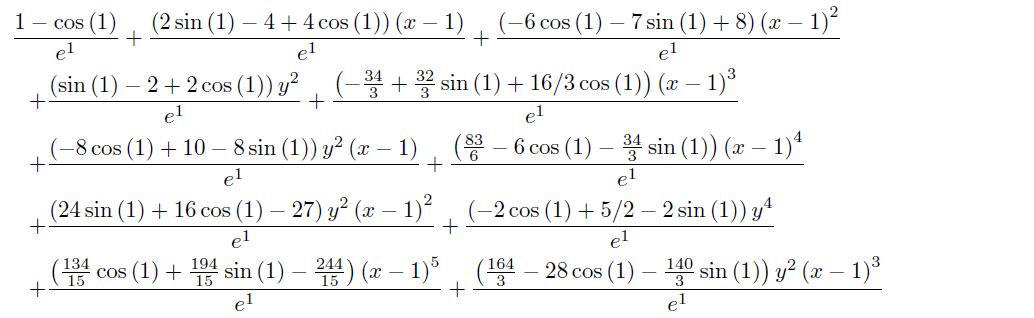
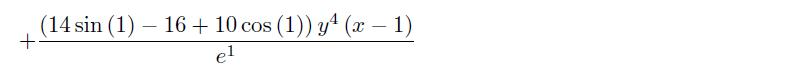
微积分问题的计算机求解系列 (0003)
试求下面级数的前 n 项及无穷项的和。
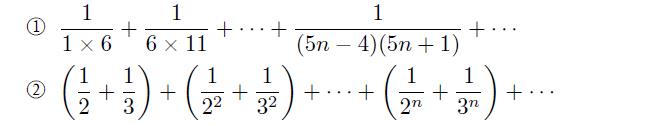
【解】 下面的语句可以直接求解级数的和。
>> syms n k; symsum(1/(5*k-4)/(5*k+1),k,1,n)
ans =
-1/5/(5*n+1)+1/5
>> symsum(1/(5*k-4)/(5*k+1),k,1,inf)
ans =
1/5
>> syms n k; symsum(1/2^k+1/3^k,k,1,n)
ans =
-2*(1/2)^(n+1)-3/2*(1/3)^(n+1)+3/2
>> symsum(1/2^k+1/3^k,k,1,inf)
ans =
3/2
当然,无穷级数的和还可以通过极限的方式求出。
拓展:
试求出下面的极限。
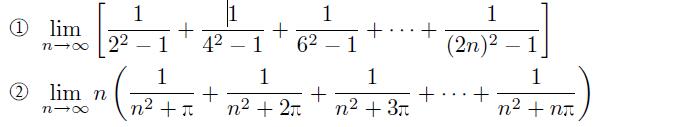
【求解】 ① 可以用下面两种方法求解。
>> syms k n; symsum(1/((2*k)^2-1),k,1,inf)
ans =
1/2
>> limit( symsum(1/((2*k)^2-1),k,1,n),n,inf)
ans =
1/2
② 可以由下面的语句直接求解。
>> syms k n limit(n*symsum(1/(n^2+k*pi),k,1,n),n,inf)
ans =
1
微积分问题的计算机求解系列 (0004)
试求下面级数的前 n 项及无穷项的和。
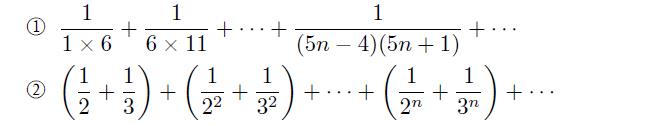
【解】 下面的语句可以直接求解级数的和。
>> syms n k; symsum(1/(5*k-4)/(5*k+1),k,1,n)
ans =
-1/5/(5*n+1)+1/5
>> symsum(1/(5*k-4)/(5*k+1),k,1,inf)
ans =
1/5
>> syms n k; symsum(1/2^k+1/3^k,k,1,n)
ans =
-2*(1/2)^(n+1)-3/2*(1/3)^(n+1)+3/2
>> symsum(1/2^k+1/3^k,k,1,inf)
ans =
3/2
当然,无穷级数的和还可以通过极限的方式求出。
拓展:
试求出下面的极限。
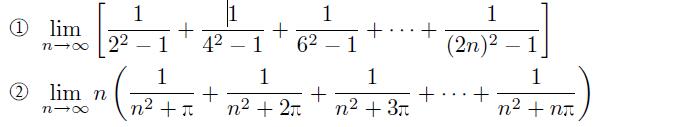
【求解】 ① 可以用下面两种方法求解。
>> syms k n; symsum(1/((2*k)^2-1),k,1,inf)
ans =
1/2
>> limit( symsum(1/((2*k)^2-1),k,1,n),n,inf)
ans =
1/2
② 可以由下面的语句直接求解。
>> syms k n limit(n*symsum(1/(n^2+k*pi),k,1,n),n,inf)
ans =
1
微积分问题的计算机求解系列 (0005)
试求出以下的曲线积分。
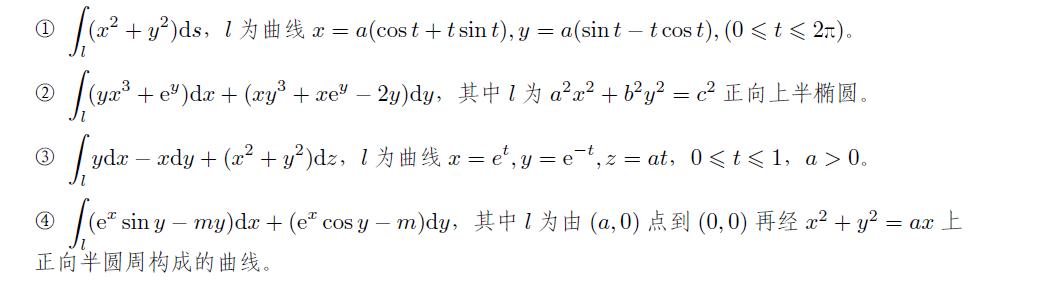
【解】
套用第一类和第二类曲线积分公式,可以直接得出曲线积分的结果。
-
需要注意的是:使用Maple内核的matlab与Mupad内核的matlab进行符号计算的结果可能表达形式是不一样。
-
个人觉得Maple的符号计算更靠谱、更强大。
>> syms a t;
x=a*(cos(t)+t*sin(t));
y=a*(sin(t)-t*cos(t));
f=x^2+y^2;
I=int(f*sqrt(diff(x,t)^2+diff(y,t)^2),t,0,2*pi)
I =
2*pi^2*(2*pi^2 + 1)*(a^2)^(3/2)
>> syms x y a b c t;
x=c*cos(t)/a;
y=c*sin(t)/b;
P=y*x^3+exp(y);
Q=x*y^3+x*exp(y)-2*y;
ds=[diff(x,t);diff(y,t)];
I=int([P Q]*ds,t,0,pi)
I =
-(2*c*(15*b^4 - 2*c^4))/(15*a*b^4)
>> syms t;
syms a positive;
x=exp(t);
y=exp(-t);
z=a*t;
F=[y, -x, (x^2+y^2)];
ds=[diff(x,t);diff(y,t);diff(z,t)];
I=int(F*ds,t,0,1)
I =
(a*exp(2))/2 - (a*exp(-2))/2 + 2
>> syms t m; syms a positive;
x1=t; y1=0;
F1=[exp(x1)*sin(y1)-m*y1, exp(x1)*cos(y1)-m];
x2=a/2+a/2*cos(t); y2=a/2*sin(t);
F2=[exp(x2)*sin(y2)-m*y2, exp(x2)*cos(y2)-m];
I1=int(F1*[diff(x1,t);diff(y1,t)],t,0,a)
I2=int(F2*[diff(x2,t);diff(y2,t)],t,0,pi);
>> I=I1+I2
I =
(pi*a^2*m)/8
以上是关于以MATLAB的方式实现微积分问题的计算机求解问题及解决方案集锦的主要内容,如果未能解决你的问题,请参考以下文章