CodeForces - 1486F Pairs of Paths(树上计数+容斥)
Posted Frozen_Guardian
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CodeForces - 1486F Pairs of Paths(树上计数+容斥)相关的知识,希望对你有一定的参考价值。
题目链接:点击查看
题目大意:给出一棵 n n n 个点的树,再给出 m m m 条路径,现在问有多少个路径对 ( x , y ) (x,y) (x,y),满足第 x x x 条路径和第 y y y 条路径有且仅有一个交点
题目分析:参考至大佬博客:https://www.cnblogs.com/syksykCCC/p/CF1486F.html
再借个图。。(侵权删)
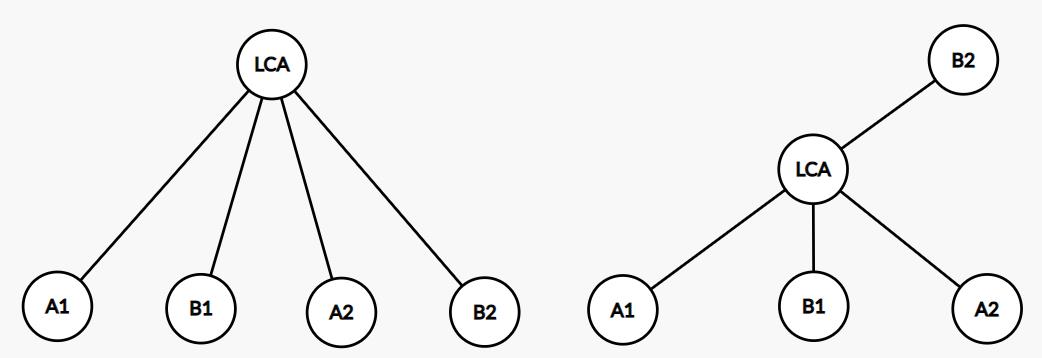
本题需要求的路径只有可能是上述两种情况,第一种是
L
C
A
LCA
LCA 相同,第二种是
L
C
A
LCA
LCA 不同,不过总而言之都需要利用
L
C
A
LCA
LCA 来辅助计数
感觉是挺套路的题,直接说做法吧,对于每条路径,我们将其抽象成五个变量即可: u , v , a , b , l c a u,v,a,b,lca u,v,a,b,lca
其中 u , v , l c a u,v,lca u,v,lca 顾名思义且很好求,就是路径两端的节点以及 L C A ( u , v ) LCA(u,v) LCA(u,v), a , b a,b a,b 储存的是点 u u u 和 v v v 分别在 l c a lca lca 的哪棵子树中,我们只需要保存一下从 l c a lca lca 到 u u u 这条路径上的第一个节点就可以了,这个用倍增也很容易求,就是需要注意一下,假如 u u u 和 l c a lca lca 是同一个点的情况,此时用 − 1 -1 −1 来表示这条路径,这里的 a , b a,b a,b 是辅助计数用的
为了防止重复计数,我们还需要最后令 ( a , b ) (a,b) (a,b) 二元对满足 a < = b a<=b a<=b
现在开始讨论如何计数,对于第一种情况比较简单,当 l c a lca lca 确定时,我们只需要求 ( a , b ) (a,b) (a,b) 二元对互不相同的对数即可,容斥一下就好了: c n t ( a , b ) 互 不 相 同 = ( 总 对 数 ) − c n t a 相 同 − c n t b 相 同 + c n t ( a , b ) 相 同 cnt_{(a,b)互不相同}=(总对数)-cnt_{a相同}-cnt_{b相同}+cnt_{(a,b)相同} cnt(a,b)互不相同=(总对数)−cnta相同−cntb相同+cnt(a,b)相同
对于第二种情况,我们其实只需要统计一下除去 a a a 和 b b b 的子树后, l c a lca lca 的子树中有多少个路径的端点即可,为了做到不重不漏,需要先统计深度较小的 l c a lca lca 然后再统计深度较大的,正确性显然,手玩一下就能明白了
最后就是实现了,第一种情况的计数,只需要开个 m a p map map 就好了,第二种情况的统计子树,维护一下 d f s dfs dfs 序然后用树状数组维护实现起来也是比较简单
代码:
// Problem: F. Pairs of Paths
// Contest: Codeforces - Codeforces Round #703 (Div. 2)
// URL: https://codeforces.com/contest/1486/problem/F
// Memory Limit: 512 MB
// Time Limit: 6000 ms
//
// Powered by CP Editor (https://cpeditor.org)
// #pragma GCC optimize(2)
// #pragma GCC optimize("Ofast","inline","-ffast-math")
// #pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<iostream>
#include<cstdio>
#include<string>
#include<ctime>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<stack>
#include<climits>
#include<queue>
#include<map>
#include<set>
#include<sstream>
#include<cassert>
#include<bitset>
#include<list>
#include<unordered_map>
#define lowbit(x) x&-x
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
template<typename T>
inline void read(T &x)
{
T f=1;x=0;
char ch=getchar();
while(0==isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(0!=isdigit(ch)) x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
x*=f;
}
template<typename T>
inline void write(T x)
{
if(x<0){x=~(x-1);putchar('-');}
if(x>9)write(x/10);
putchar(x%10+'0');
}
const int inf=0x3f3f3f3f;
const int N=3e5+100;
vector<int>node[N];
int dp[N][25],deep[N],L[N],R[N],dfn=0;
int c[N];
struct Path {
int u,v,a,b,lca;
bool operator<(const Path& t) const {
if(deep[lca]!=deep[t.lca]) {
return deep[lca]<deep[t.lca];
}
return lca<t.lca;
}
}p[N];
void dfs(int u,int fa,int dep) {
L[u]=++dfn;
deep[u]=dep;
dp[u][0]=fa;
for(int i=1;i<=20;i++) {
dp[u][i]=dp[dp[u][i-1]][i-1];
}
for(auto v:node[u]) {
if(v==fa) {
continue;
}
dfs(v,u,dep+1);
}
R[u]=dfn;
}
int get_fa(int u,int x) {
if(x>=0) {
for(int i=0;i<=20;i++) {
if((x>>i)&1) {
u=dp[u][i];
}
}
}
return u;
}
int LCA(int x,int y) {
if(deep[x]<deep[y]) {
swap(x,y);
}
for(int i=20;i>=0;i--) {
if(deep[x]-deep[y]>=(1<<i)) {
x=dp[x][i];
}
}
if(x==y) {
return x;
}
for(int i=20;i>=0;i--) {
if(dp[x][i]!=dp[y][i]) {
x=dp[x][i];
y=dp[y][i];
}
}
return dp[x][0];
}
void add(int x) {
for(int i=x;i<N;i+=lowbit(i)) {
c[i]++;
}
}
int ask(int x) {
int ans=0;
for(int i=x;i>0;i-=lowbit(i)) {
ans+=c[i];
}
return ans;
}
int query(int l,int r) {
return ask(r)-ask(l-1);
}
int main()
{
#ifndef ONLINE_JUDGE
// freopen("data.in.txt","r",stdin);
// freopen("data.out.txt","w",stdout);
#endif
// ios::sync_with_stdio(false);
int n;
read(n);
for(int i=1;i<n;i++) {
int u,v;
read(u),read(v);
node[u].push_back(v);
node[v].push_back(u);
}
dfs(1,0,0);
int m;
read(m);
for(int i=1;i<=m;i++) {
read(p[i].u),read(p[i].v);
int u=p[i].u,v=p[i].v;
int lca=LCA(u,v);
p[i].lca=lca;
int fu=get_fa(u,deep[u]-deep[lca]-1);
int fv=get_fa(v,deep[v]-deep[lca]-1);
p[i].a=(lca==fu)?-1:fu;
p[i].b=(lca==fv)?-1:fv;
if(p[i].a>p[i].b) {
swap(p[i].a,p[i].b);
}
}
sort(p+1,p+1+m);
LL ans1=0,ans2=0;
for(int i=1;i<=m;i++) {
int j=i;
while(p[i].lca==p[j].lca) {
j++;
}
map<int,int>cnt1;
map<pair<int,int>,int>cnt2;
for(int k=i;k<j;k++) {//[i,j) lca is same
int lca=p[k].lca,a=p[k].a,b=p[k].b;
ans1+=(k-i);
if(a!=-1) {
ans1-=cnt1[a];
cnt1[a