2021CCPC湘潭全国邀请赛题解

Posted 2021-06-26 yueshehanjiang

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了2021CCPC湘潭全国邀请赛题解相关的知识，希望对你有一定的参考价值。

题目pdf下载
提取码: abcd
其他题最近会慢慢写出来
一共A了5题，j题签到题没出来，如果罚时少一点并且把J也写了的话，也许就金了

A. A+B Problem

题意：

给定a和b，求a+b,a+b如果大于1023或者小于-1024，就自动溢出

思路：模拟

比如1023+1=1024，1024>1023 就自动溢出成-1024，模拟即可

时间复杂度：O n

#include<bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define re register int
#define pll pair<int,int> 
#define x first 
#define y second 
#define sf(x) scanf("%d",&x)
#define sfl(x) scanf("%lld",&x)
typedef long long ll ;
using namespace std;
const int N =  1e6 + 10 , M = 1010 , inf = 0x3f3f3f3f , mod = 1e9 + 7 ;

int main()
{
    int t ;
    cin >> t ;
    while(t--)
    {
        int a , b ;
        cin >> a >> b ;
        int k = a + b ;
        if(k > 1023) k -= 2048 ;
        else if(k < -1024) k += 2048 ;
        cout << k << "\\n" ;
    }
    return 0;
}

思路：数论分块
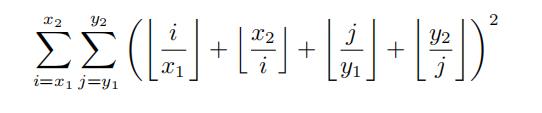
在这里插入图片描述
一维数论整除分块
第4个式子的答案有点问题
对其每一个区间左端点为l，右端点为r，值为cnt
答案为(r-l+1) $\\times$ cnt $\\times$ $\\sum_{i=x1}^{x2} {\\lfloor \\frac{i}{x1} \\rfloor}$
在考虑一下求
$\\sum_{i=x1}^{x2} {\\lfloor \\frac{i}{x1} \\rfloor}$

可以发现，
当x1<=i<2*x1 ，i/x1等于1
当2*x1<=i<3*x1,i/x1等于2
...........
当n*x1<=i<(n+1)*x1 , i/x1等于n
因此答案为 x1 * (1 + 2 + ........ + n ) + 大于等于(n+1)*x1的部分暴力求
在考虑一下1式
答案为 x1 * (1^2 + 2^2 + ........ + n^2) + 大于等于(n+1)*x1的部分暴力求
中间括号的部分用公式o1求即可

时间复杂度：O t $\\sqrt{n}$

E. CCPC Strings

题意：

给一个整数n，会有2^n个不同的cp字符串
求每个不同字符串的ccpc子串的个数的总和
答案对1e9+7取膜

思路：bm算法求线性通项公式

先暴力预处理前20项
然后在用bm算法求出线性递推方程
o1输出即可

时间复杂度：20 * 2^20 + t

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <cassert>
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1000000007;
ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
// head
 
int _;
ll n;
namespace linear_seq {
    const int N=10010;
    ll res[N],base[N],_c[N],_md[N];
 
    vector<int> Md;
    ll mul(ll *a,ll *b,int k) {
        rep(i,0,k+k) _c[i]=0;
        rep(i,0,k) if (a[i]) rep(j,0,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
        for (int i=k+k-1;i>=k;i--) if (_c[i])
            rep(j,0,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
        rep(i,0,k) a[i]=_c[i];
    }
    ll solve(ll n,VI a,VI b) { // a 绯绘暟 b 鍒濆€?b[n+1]=a[0]*b[n]+...
//        printf("%d\\n",SZ(b));
        ll ans=0,pnt=0;
        int k=SZ(a);
        assert(SZ(a)==SZ(b));
        rep(i,0,k) _md[k-1-i]=-a[i];_md[k]=1;
        Md.clear();
        rep(i,0,k) if (_md[i]!=0) Md.push_back(i);
        rep(i,0,k) res[i]=base[i]=0;
        res[0]=1;
        while ((1ll<<pnt)<=n) pnt++;
        for (int p=pnt;p>=0;p--) {
            mul(res,res,k);
            if ((n>>p)&1) {
                for (int i=k-1;i>=0;i--) res[i+1]=res[i];res[0]=0;
                rep(j,0,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i,0,k) ans=(ans+res[i]*b[i])%mod;
        if (ans<0) ans+=mod;
        return ans;
    }
    VI BM(VI s) {
        VI C(1,1),B(1,1);
        int L=0,m=1,b=1;
        rep(n,0,SZ(s)) {
            ll d=0;
            rep(i,0,L+1) d=(d+(ll)C[i]*s[n-i])%mod;
            if (d==0) ++m;
            else if (2*L<=n) {
                VI T=C;
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                L=n+1-L; B=T; b=d; m=1;
            } else {
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    ll gao(VI a,ll n) {
        VI c=BM(a);
        c.erase(c.begin());
        rep(i,0,SZ(c)) c[i]=(mod-c[i])%mod;
        return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
    }
};
 
int main() {
        int t;
        scanf("%d",&t);
        vector<int>v;
        for(int i=1;i<=20;i++){
        	ll ans=0;
        	char s[22];
        	s[i]=0;
        	for(int j=0;j<(1<<i);j++){
        		for(int k=0;k<i;k++){
        			if((1ll<<k)&j){
        				s[k]='C';
        			}
        			else s[k]='P';
        		}
//        		cout<<s<<endl;
        		for(int k=0;k+3<i;k++){
        			if(s[k]=='C'&&s[k+1]=='C'&&s[k+2]=='P'&&s[k+3]=='C'){
        				ans++;
        				k=k+3;
        			}
        		}
        	}
        	//printf("%lld\\n",ans);
        	v.push_back(ans);
        }
    while (t--) {
        scanf("%lld",&n);
        printf("%lld\\n",linear_seq::gao(v,n-1));
    }
}

G. Game

题意：

给定n个在set里面的数，每次可以进行一次操作
将set里面的其中一个数x变成 x-9 / x-99 / x-999 / ........ /x − (10^k − 1) 
保证x − (10^k − 1) > 0
并且每个数在set里面不能同时出现多次
A先操作，然后B操作，谁最后不能操作就输，问谁赢

思路：数论，贪心

性质1：任何一个数都可以表示成9*a+b的形式
性质2：如果减去一个数，一定只减9,因为减99等价于减去了11个9
所以都是奇数次操作，不影响最后的答案
性质3：从最小的数开始减，减到不能减为止
前2个性质都比较好推，说一下第三个是怎么推出来的
比如 111 * 9 + 1 和 11 * 9 + 1 我们考虑一下顺序
如果先减111 * 9 + 1的话，会发现只能减到12 * 9 + 1 
在减的话变成11 * 9 + 1 ，与另外一个11 * 9 + 1冲突
所以从最小的开始减，减到0*9+1，第二个数减到1*9+1，以此类推。
最后统计一下操作数
如果操作数为偶数，B赢
否则，A赢

时间复杂度：O tnlogn

#include<bits/stdc++.h>
#define fer(i,a,b) for(re i = a ; i <= b ; ++ i)
#define re register int
#define pll pair<int,int> 
#define x first 
#define y second 
#define sf(x) scanf("%d",&x)
#define sfl(x) scanf("%lld",&x)
typedef long long ll ;
using namespace std;
const int N =  1e5 以上是关于2021CCPC湘潭全国邀请赛题解的主要内容，如果未能解决你的问题，请参考以下文章 
 2021CCPC湘潭全国邀请赛题解
 2021CCPC湘潭邀请赛复盘
 2021CCPC湘潭邀请赛复盘
 [CCPC2017]湘潭邀请赛
 [题解]2018湘潭邀请赛
 CCPC2018-湖南全国邀请赛

2021CCPC湘潭全国邀请赛题解

A. A+B Problem

C. Calculate

E. CCPC Strings

G. Game