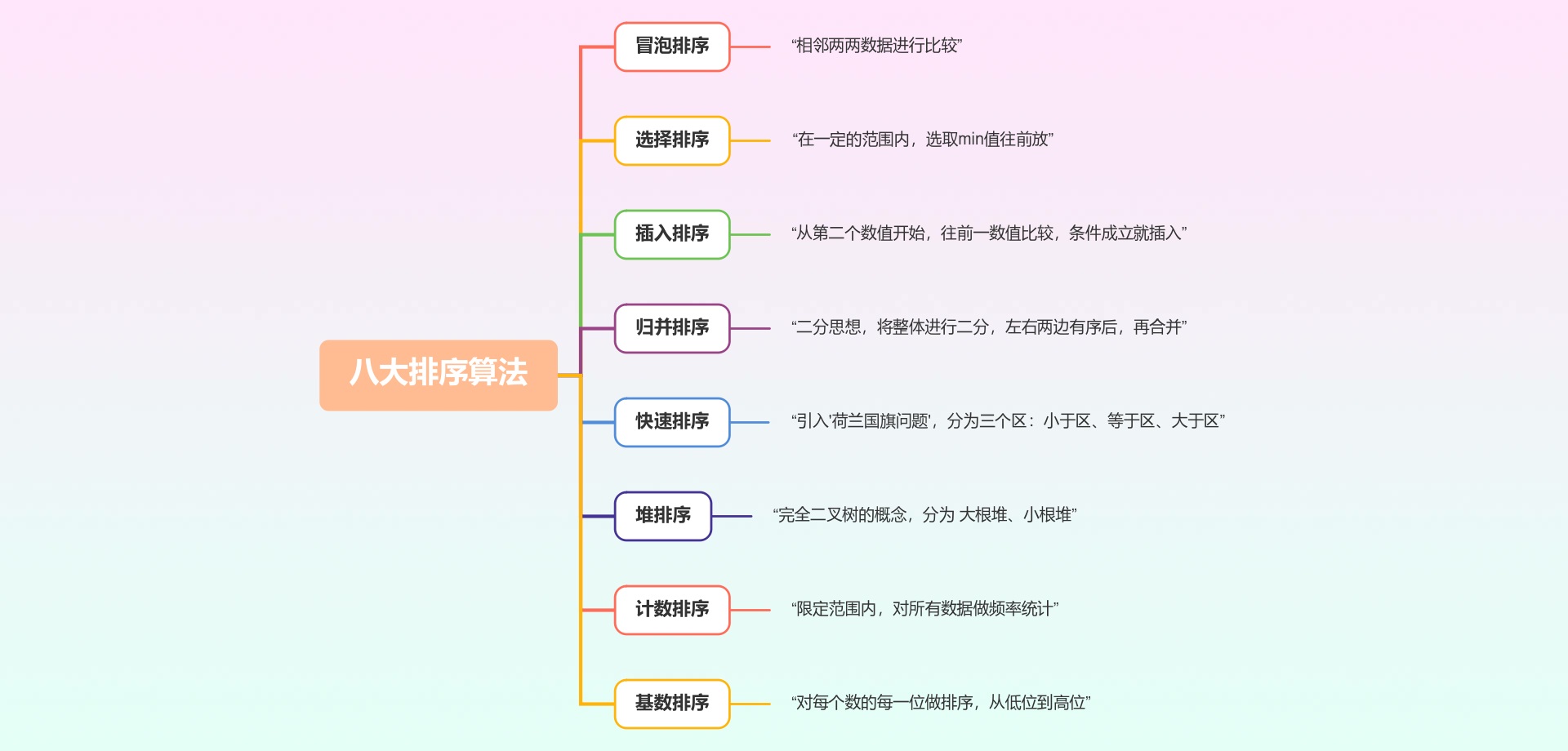
从此不再无序:八大排序算法总结(附JavaC源码)
Posted 飞人01_01
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从此不再无序:八大排序算法总结(附JavaC源码)相关的知识,希望对你有一定的参考价值。
前言
大家好!今天小编整理一下面试官常考的一大热点题型:“排序”。下面的文章将重点的几大排序做了解析,我们从冒泡、选择、插入、归并、快速、堆、计数和基数这八大经典的排序算法讲起,比如:希尔排序,在插入排序的基础上做了优化,本文就不在讲解,博客网站上有很多文章!!!
大部分公司都会注重查找和排序算法。应聘者可以在了解各种查找和排序算法的基础上,重点掌握二分查找、归并排序和快速排序。 还要对各种排序算法的时间、空间复杂度烂熟于心,了解它的优缺点。
我参考的文章有:十大经典排序算法总结(Java实现+动画) 和 十大经典排序算法动画 和《大话数据结构》
Java语言源码:GitHub
C语言源码:Github
开始之前,先简单认识一下排序和相关术语的概览吧。
排序:假设含有n个记录(数据元素)的序列为{R1,R2,……,Rn},其相应的关键字分别为{k1,k2,……,kn},需确定1,2,……,n的一种排列p1,p2,……,pn,使其相应的关键字满足Kp1 <= Kp2 <= …… <=
Kpn 非递减(非递增)关系,即使序列成为一个按关键字有序的序列,这样的操作称为排序。
稳定性: 假设Ki = Kj(i和j都在区间[1,n],且i 不等于j),并且在排序前的序列中Ri 领先于Rj(即i<j)。 如果排序后Ri仍然领先于Rj,则称所用的排序方法是稳定的;反之,则称所用的排序方法是不稳定的。
内排序与外排序:内排序是在排序整个过程中,待排序的所有数据全部被放置在内存中。外排序是由于排序的数据个数太多不能同时放置在内存中,整个排序过程需要在内外存之间多次交换数据才能进行。
这里我们先把swap交换函数给实现了,等会一下的代码就直接调用这个函数。
void swap(int arr[], int L, int R)
{
int tmp = arr[L];
arr[L] = arr[R];
arr[R] = tmp;
}
文章目录
一、冒泡排序 (Bubble Sort)
冒泡排序:两两比较相邻的数据,如果反序则交换,直到没有反序的数据为止。
在实现冒泡排序的细节上,我们分为两种冒泡排序:初级版与改进版。
动图演示:
//冒泡排序初级版
void BubbleSort(int arr[], int arrLength)
{
int i = 0;
for (i = 0; i < arrLength - 1; i++) //循环的躺数
{
int j = 0;
for (j = 0; j < arrLength - 1 -i; j++) //一趟需要交换数据的对数
{
if(arr[j] > arr[j+1]) //升序
swap(arr, j, j+1);
}
}
}
解析:第5行的for循环,控制了这组数据需要进行多少趟,上面动图中,第一次循环“48”在前面的位置,最后来到倒数第二的位置上,这样一次,我们称为一趟排序。假设这个arr数组共有10个元素,则整个循环完成,只需要循环9趟即可完成排序。(arrLength - 1)
第8行的for循环,控制了这一趟中,有多少对数据进行比较大小,例如:arr数组共有10个元素,第一趟我们只需要比较9对元素,就能让最大的元素来到数组的末尾;第二趟,此时最大的元素已经来到了数组的末尾,我们就不需要再对它进行判断大小了。所以,第二层循环是跟着第一层循环的改变而改变的。
第一趟: 比较9对元素
第二趟:比较8对元素
……
综上:第二层循环的停止条件为 (arrLength - 1 - i)。
初级版的冒泡我们就叙述忘了,大家是否能够发现一些问题???
例如: 待排序的元素为 {2,1,3,4,5,6,7,8,9,10},此时我需要对这个10个元素排为升序,我们观察发现,只需要2和1交换位置,整个数组就是升序了。但我们的初级版冒泡排序会怎么样?
当第一趟排序执行完后,数组的情况是{1,2,3,4,5,6,7,8,9,10}。此时程序会停下来吗???
当然不会,它还是会“傻傻”的一直在循环判断,此时我们的算法就不是那么的高效,所以我们在初级版冒泡排序的基础上,加上了一个bool值,flag。
//冒泡排序改进版
void BubbleSort(int arr[], int arrLength)
{
if (arr == NULL)
return; //空指针,提前退出
int i = 0;
int flag = 0; //因为C语言没有bool类型,就以整形代替。
for (i = 0; i < arrLength - 1 && flag != 1; i++) //一次循环完后,flag还是1,则有序
{
int j = 0;
flag = 1;
for (j = 0; j < arrLength - 1 -i; j++)
{
if(arr[j] > arr[j+1]) //升序
{
swap(arr, j, j+1);
flag = 0; //如果if语句进来后,则说明当前数组还是无序的
}
}
}
}
二、选择排序 (Selection Sort)
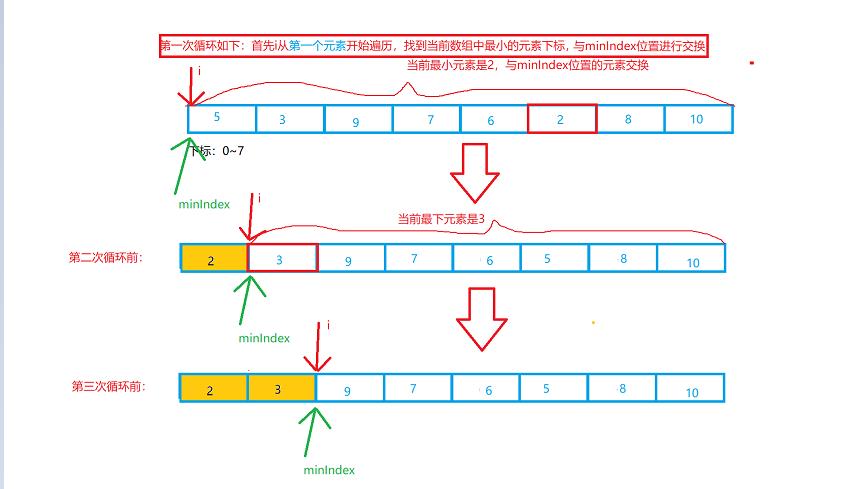
选择排序:通过n-i次元素之间的比较,从n-i+1个元素中选出最小(最大)的元素,跟第i个元素交换。
简单来说:看图。
void selectSort(int arr[], int arrLength)
{
if (arr == NULL)
return; //空指针,提前退出
int i,j,minIndex;
for (i = 0; i < arrLength; i++)
{
minIndex = i;
for (j = i + 1; j < arrLength; j++)
{
if (arr[minIndex] < arr[j])
minIndex = j; //保存最小值的下标
}
if (minIndex != i)
swap(arr, minIndex, i); //如果minIndex不是i,说明有最小值
}
}
三、插入排序 (Insert Sort)
插入排序:将一个数据插入到已经排好序的有序表中,从而得到一个新的、数据个数增1的有序表。
动图演示:
void insertSort(int arr[], int arrLength)
{
if (arr == NULL)
return; //空指针,提前退出
int i = 0;
int j = 0;
for (i = 1; i < arrLength; i++)
{
int insertValue = arr[i];
for (j = i - 1; j >= 0 && insertValue < arr[j]; j--) //insertValue < arr[j]
{
arr[j + 1] = arr[j]; //前一个数据往后移动
}
if (insertValue != arr[i]) //如果经过循环后,这两个不相等,说明循环里面移动过数据
arr[++j] = insertValue; //这里值得注意的是,for循环停止时,j-- 已经自减了
}
}
插入排序,就像我们过年时,几个小伙伴一起斗地主一样,每从桌上拿起一张牌,我们就会按照3 4 5 6 7……J Q K A,的顺序进行排列。插入的过程中,其余的牌就要整体移动,给插入的这张牌让一个位置。

四、归并排序 (Merger Sort)
归并排序:就是将一组数据进行二分拆开成左、右两个数组,分别使左右两个数组有序后,再合并到一起。
将大问题拆分为小问题,然而小问题也可以拆分为更小的问题,可以考虑递归函数。
先看动图:

//递归解法
#define MAXNUM 20 //数组最大元素个数
void mergerSort1(int arr[], int left, int right)
{
if (arr == NULL || left == right)
return;
int mid = left + ((right - left) >> 1); //取中间数,也就是 (left + right)/2
mergerSort(arr, left, mid); //递归调用左数组
mergerSort(arr, mid+1, right); //递归调用右数组
merger(arr, left, mid, right); //左右数组分别有序后,合并到一起
}
void merger(int arr[], int left, int mid, int right)
{
int help[MAXNUM]= {0}; //用于临时存储两个数组合并时的有序数组
int i = 0; //指向help数组
int p1 = left; //指向左数组
int p2 = mid + 1; //指向右数组
while (p1 <= mid && p2 <= right)
help[i++] = arr[p1] < arr[p2]? arr[p1++] : arr[p2++]; //谁更小,就放入help数组
while (p1 <= mid) //左边数组还有数据,就放入help
help[i++] = arr[p1++];
while (p2 <= right) //右边数组还有数据,就放入help
help[i++] = arr[p2++];
//将help数组的所有数据按照顺序放入原数组arr
int j = 0;
for (j = 0; j < i; j++)
arr[left+j] = help[j]; //注意是从left位置处开始拷贝
}
将整个数组分成小块,将每个小块的数据变为有序后,再合并起来,这就是归并。
想要写降序,第20行的三目操作符修改一下就可以!
还有就是第7行的取中间数,为什么要这样写??两点原因
- 位运算的速度远快于普通的加减乘除!
- 考虑溢出的情况,例如int最大的32亿左右,如果此时我的left是19亿,right是19亿,此时二者相加就溢出了整形的范围。
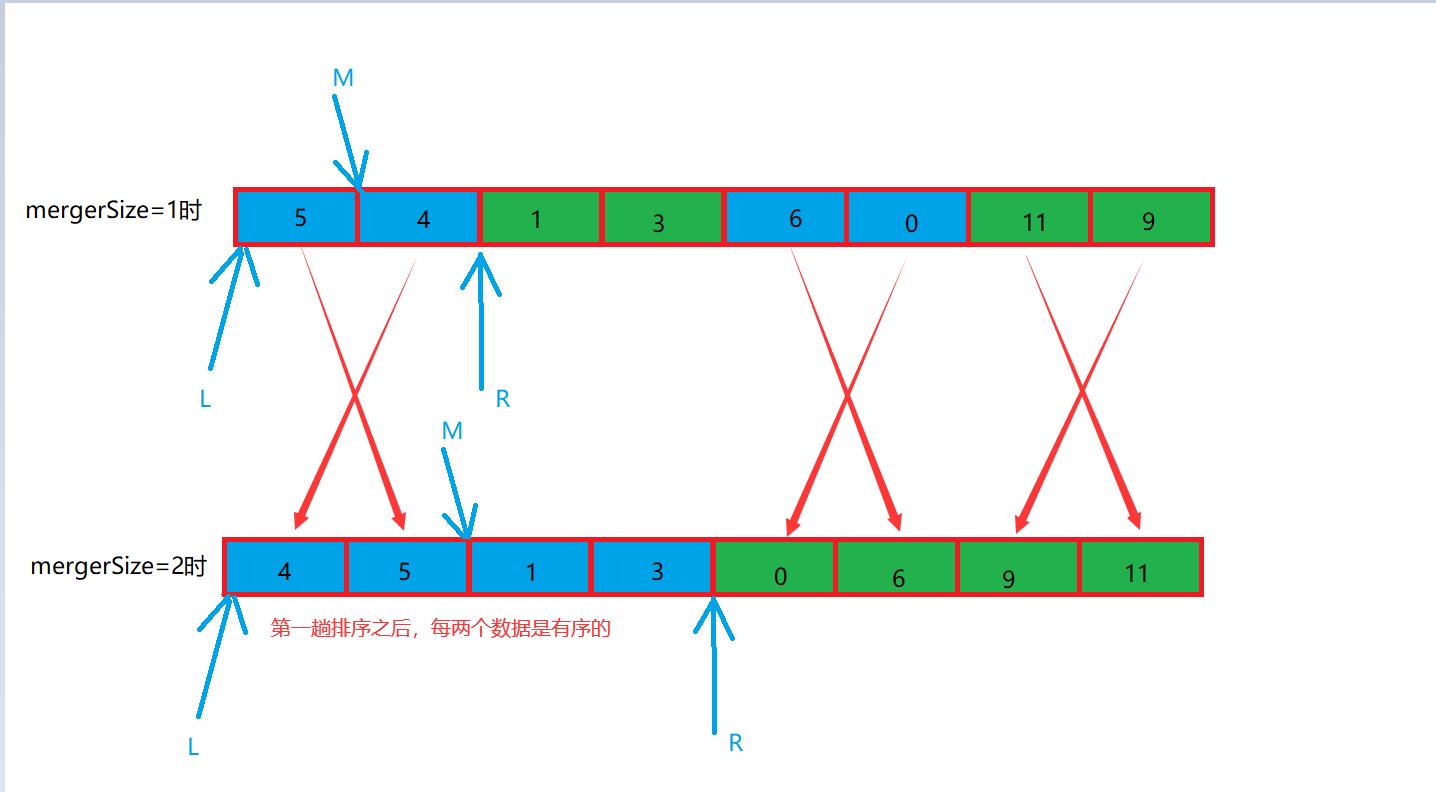
//非递归解法
void mergerSort2(int arr[],int arrLength)
{
int mergerSize = 1; //表示左数组的元素个数,最开始时,左边元素个数1个,右边也为1个
while (mergerSize < arrLength)
{
int L = 0;
while (L < arrLength) //一趟
{
int M = L + mergerSize - 1; //取中间值
if(M >= arrLength)
break; //如果中间值大于等于数组的长度,则提前退出
//取右边数组的范围
int R = (M + mergerSize) < (arrLength - 1)? M+mergerSize:arrLength-1;
merger(arr,L,M,R); //还是调用归并函数
L = R + 1;
}
if(mergerSize > arrLength / 2)
return; //防止整形溢出,提前判断一下
mergerSize <<= 1; //乘2 mergerSize = mergerSize * 2;
}
}
void merger(int arr[], int left, int mid, int right)
{
int help[MAXNUM]= {0}; //用于临时存储两个数组合并时的有序数组
int i = 0; //指向help数组
int p1 = left; //指向左数组
int p2 = mid + 1; //指向右数组
while (p1 <= mid && p2 <= right)
help[i++] = arr[p1] < arr[p2]? arr[p1++] : arr[p2++]; //谁更小,就放入help数组
while (p1 <= mid) //左边数组还有数据,就放入help
help[i++] = arr[p1++];
while (p2 <= right) //右边数组还有数据,就放入help
help[i++] = arr[p2++];
//将help数组的所有数据按照顺序放入原数组arr
int j = 0;
for (j = 0; j < i; j++)
arr[left+j] = help[j]; //注意是从left位置处开始拷贝
}
非递归与递归二者的区别?
当我们递归调用到数据的最底层,最先移动的数据还是下标为0和下标为1的数据,这二者进行比较,此时,其他的参数在栈区里面保存着,当这两个数据操作完成之后,才返回函数,去进入下一个下标2、3的数据进行比较和排序。
反观非递归的解法,则直接定义最开始时,左右数组的元素个数(mergerSize),当下标为0、1的数据操作之后,L直接跳到2、3的位置,一趟排序之后,此时数组中每两个数据是有序的; 此时扩大mergerSize为2,即就是左右数组大小各为2,再次重复上面的操作。
五、快速排序 (Quick Sort)
在讲解快速排序问题之前,我们先了解一下“荷兰国旗问题”。
从上面的这个题目,我们可以提取出一些算法思想。
假设待排序的数组是{10, 30, 50, 40, 20, 60, 40},我们将数组的最后一个元素40作为“中心点”,将数组中的所有数据都跟“中心点”(40)做比较,比中心点小的,放到数组的前面,比中心点大的放到数组的后面,等于中心点的放到中间。 这样,我们将整个数组分为了三个区域:< 区、= 区、> 区。
经过上面的步骤得到以下数组:
- {10,30,20,40,60,50,40}; 此时蓝色区域就是 < 区,绿色区域就是 >区。
- 此时将数组最后一个元素40与绿色区域的第一个元素交换位置
- 得到{10,30,20 ,40,40, 50,60};
现在看上去,整体从左到右就是一个升序,至于 <区 和 >区 再重复以上步骤就能使其有序。又是递归函数
画图理解一下其中的算法思想,这样才更容易下面的代码!!!
void quickSort(int arr[], int arrLength)
{
if (arr == NULL || arrLength < 2)
return;
process(arr, 0, arrLength - 1);
}
void process(int arr[], int left, int right)
{
if (left >= right)
return;
//随机数srand放入主函数
swap(arr, left + rand() % (right - left + 1), right); //从数组中随机抽取一个元素与数组最后的元素交换位置
//这里也是快排时间复杂度变为O(N logN)的原因
int LMid, RMid; //三个区中,等于区的第一个元素下标,和最后一个元素下标----也就是上面文字解释中的{40,40}的下标
netherlandsFlag(arr, left, right, &LMid, &RMid); //就是上面解释的,将数组分为三个区
process(arr, left, LMid - 1); //递归调用 <区的数据,上面文字解释中的 {10,30,20}
process(arr, RMid + 1, right); //递归调用 >区的数据,上面文字解释中的 {50,60}
}
void netherlandsFlag(int arr[], int left, int right, int* LMid, int* RMid)
{
if (left > right)
{
*LMid = *RMid = -1;
return;
}
if (left == right)
{
*LMid = *RMid = left;
return;
}
int minRange = left - 1; //<区范围
int maxRange = right; //>区范围,将最后一个元素先放到>区范围,总共整体排序后,与>区的第一个元素交换
int index = left; //循环判断的索引值
while (index < maxRange) //索引值不跟>区范围遇到,循环继续
{
if (arr[index] < arr[right])
swap(arr, index++, ++minRange); //放入<区,过后,索引值index++
else if (arr[index] > arr[right])
swap(arr, index, --maxRange); //放入>区,过后,索引值不变,因为从>区过来的值还不知道是大是小,所以还需要判断
else
index++; //相等的话,不交换,索引值index++即可
}
swap(arr, maxRange, right); //>区的第一个元素与数组的最后一个元素交换
*LMid = minRange + 1; //等于区的第一个元素
*RMid = maxRange; //等于区的最后一个元素
}
快速排序的时间复杂度能优化到O(N logN),最为关键的就是第14行的交换函数!!!
只有当“中心点”取到数组正中间时,此时的时间复杂度才是最好的,当取到数组的两边时,时间复杂度就很高了。所以加了随机数,使之“中心点”在数组中的出现是等概率的,具体的证明方式,就得看数学功底了!!!
六、堆排序 (Heap Sort)
将堆排序之前,我们先来了解了解“完全二叉树”是个什么!!!
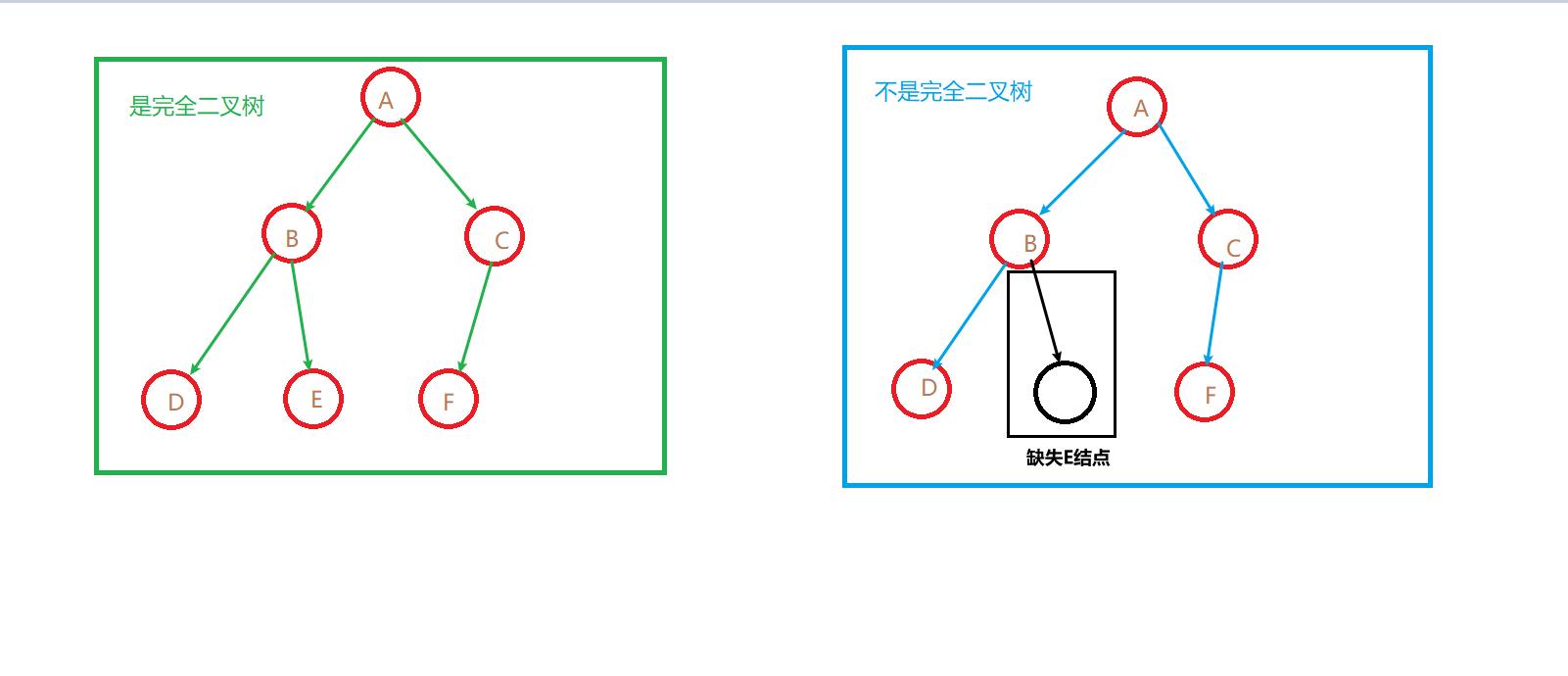
如上图所示
左边是完全二叉树,判断的理由是: 整棵树从上到下,从左到右,没有缺失结点。
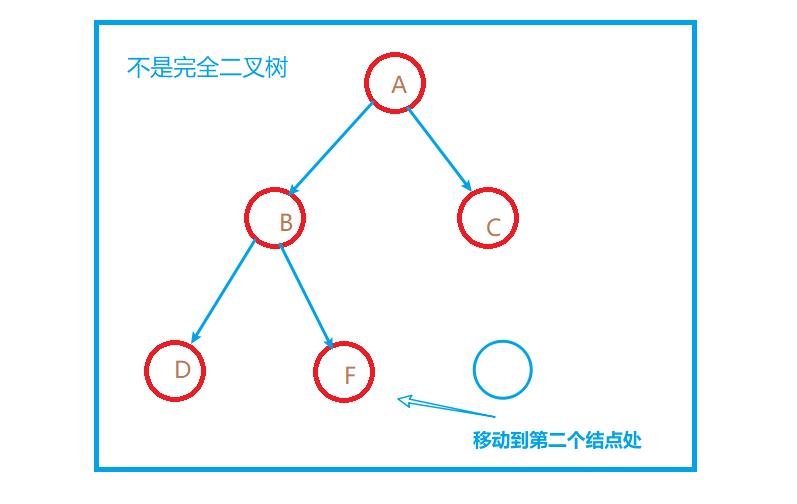
右边则不是完全二叉树:理由是: 整颗树从上到下,从左到右,在第三层第二个结点处断了,而第三个结点又还在,形成了一个“空位”,则不是完全二叉树。若将第三层的第三个结点移动到这一层第第二个结点处,则就会变为完全二叉树,如下图:
了解了完全二叉树。 我们就直接进入正题。以大根堆为例,小根堆就是改一下条件即可!
大根堆:顾名思义,就是将数值大的作为根,有以下性质:
- 左孩子结点 小于或等于 根结点。
- 右孩子结点 大于或等于 根结点。
将整个数组变为大根堆之后,此时根结点当前数组中最大的数值,我们就把他取出来,与数组的最后一个元素进行交换即可。
这里需要处理的问题就是:
- 取出根结点的值后,如何让整颗树还是保持大根堆的形式??
带着这个问题,我们来看代码。

void heapSort(int arr[], int arrLength)
{
if(arr == NULL || arrLength < 2)
return;
int i = 0;
for (i = 0; i < arrLength; i++)
heapInsert(arr, i); //大根堆的形式插入
//经过上面的循环之后,形成了大根堆。此时就将根结点的数据与数组中最后一个元素进行交换
//交换之后,根结点的数据并不是此时这颗树的最大值,所有将这个结点的数据往下层移动
int heapSize = arrLength;
swap(arr,0,--heapSize);
while (heapSize > 0)
{
heapify(arr,0,heapSize); //判断左右孩子结点和根结点的关系,条件成立,就往下层移动
swap(arr,0,--heapSize);
}
}
void heapInsert(int arr[], int index)
{
//数组是以下标为0处开始放入数据的
//则根结点和左右孩子有以下关系
//index 的根结点index/2, index的 左孩子为index*2+1,右孩子就是index*2+2
//新插入的结点,插入到叶子结点处,然后去寻找父节点,判断二者之间的大小,比父节点大的话,就要往上移动
while (arr[index] > arr[(index-1) / 2])
{
swap(arr,index,(index-1) / 2);
index = (index-1) / 2;
}
}
void heapify(int arr[], int index, int heapSize)
{
int leftChild = index * 以上是关于从此不再无序:八大排序算法总结(附JavaC源码)的主要内容,如果未能解决你的问题,请参考以下文章