python机器学习之数据探索

Posted 2021-06-26 柳小葱

🐱今天我们来讲解数据建模之前需要处理的工作，也就是数据探索的过程，很多同学会说，不就是处理缺失值，异常值，然后标准化吗？最后直接代入模型。其实大家说的也没错，但是今天我想更系统地从统计学的角度来展示一下数据探索的全过程，让我们接着下聊👇:
🐶就如我们之前说到的，机器学习也叫作统计学习，是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。我们虽然在拿到数据后直接运用机器学习的模型进行训练，这样也能得出效果，但是当模型测试集的loss过大时，你是否想过模型分布不一致，模型不够复杂，模型的optimization不够好等问题.

数据探索流程：

• • 1.查看数据集
  • 2.缺失值处理
  • 3.异常值的处理
  • 4.判断高斯分布
  • 5.训练集和测试集的分布
  • 6.判断线性相关
  • 7.变量的相关性
  • 8.Box-Cox变换

1.查看数据集

数据集的查看这一部分就很简单

#导入数据，编码方式为utf-8，每个字段的分割符为一个tab
import pandas as pd
train_data=pd.read_csv(r"C:\\Users\\Administrator\\Desktop\\zhengqidata\\zhengqi_train.txt",encoding="utf-8",sep="\\t")
test_data=pd.read_csv(r"C:\\Users\\Administrator\\Desktop\\zhengqidata\\zhengqi_test.txt",encoding="utf-8",sep="\\t")
#查看数据集的基本信息
train_data.info()

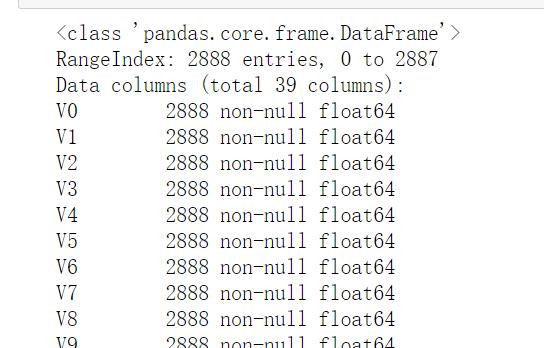
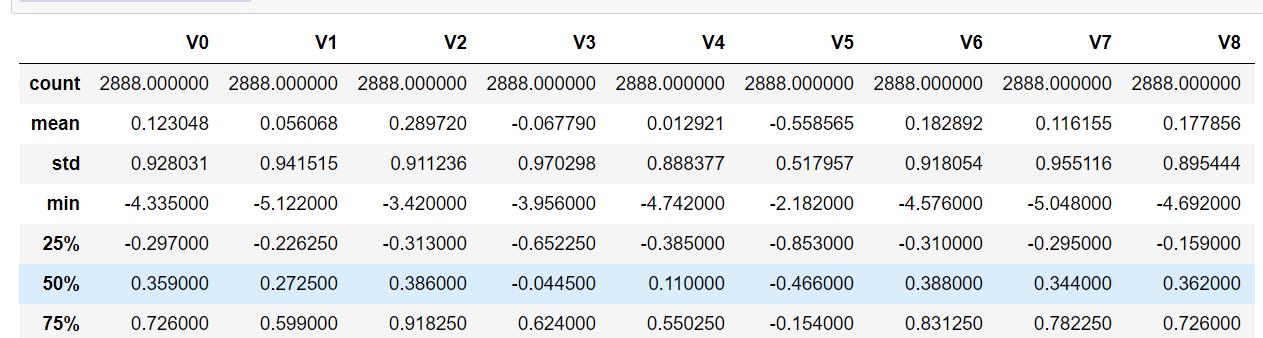
#查看训练集统计信息 主要包括样本数、均值、标准差、最大值，最小值、分位点等信息
train_data.describe()

数据集信息的展示：

#查看前几列数据
train_data.head()

结果如下：

2.缺失值处理

对于数据中缺失值的处理主要分为以下几个方面：

• 删除缺失值：将含有缺失值的行删除
• 填补缺失值：利用平均数、众数和中位来填补，也可以使用预测模型来填补。

3.异常值的处理

异常值是指远远偏离整个样本总体的观测值；异常值我们通常采用箱线图来处理，处在上下限之外的数据都都属于异常值。处理的方式：

• 删除：如果是由于输入误差、数据处理误差引起的异常值，或者异常值很小，则可以直接将其删除。
• 转换：数据转换可以消除异常值，如对数据取对数会减轻由极值引起的变化。
• 填充:就像处理缺失值一样，我们可以对异常值进行修改，如使用平均值，中值或者其他方法进行填充。
• 区别对待

#箱线图：箱线图是用来处理异常值值的，通常将远远偏离整个样本总体的观测值称为异常值
#先画出v0特征的箱线图
fig=plt.figure(figsize=(4,6))#指定画布的宽度和高度
sns.boxplot(train_data['V0'],orient="v",width=0.5)

我们先画出一个特征的箱线图

#箱线图：箱线图是用来处理异常值值的，通常将远远偏离整个样本总体的观测值称为异常值
#先画出v0特征的箱线图
fig=plt.figure(figsize=(4,6))#指定画布的宽度和高度
sns.boxplot(train_data['V0'],orient="v",width=0.5)

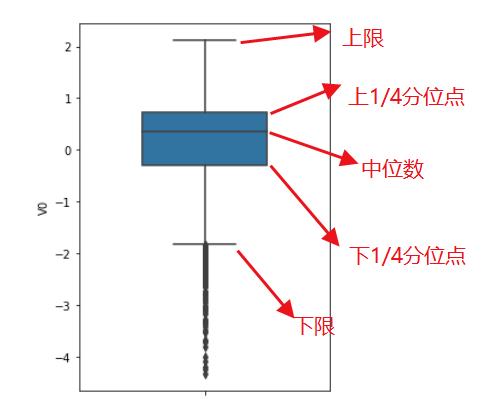
画出所有特征的箱线图

#把所有特征的箱线图画出来
column=train_data.columns.tolist()
plt.figure(figsize=(80,60))
for i in range(len(column)):
    plt.subplot(6,8,i+1)#将画布分割为6行8列
    sns.boxplot(train_data[column[i]],orient="v",width=0.5)#每一个小区域画出箱型图
    plt.xlabel(column[i],fontsize=36)#x轴的注释为xlabel
plt.show()

结果如下：

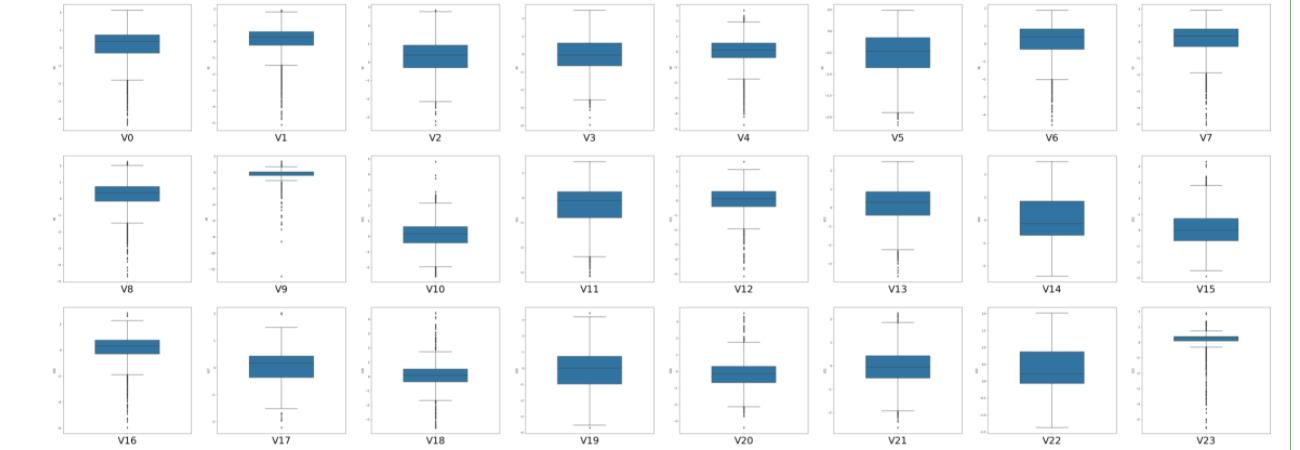
4.判断高斯分布

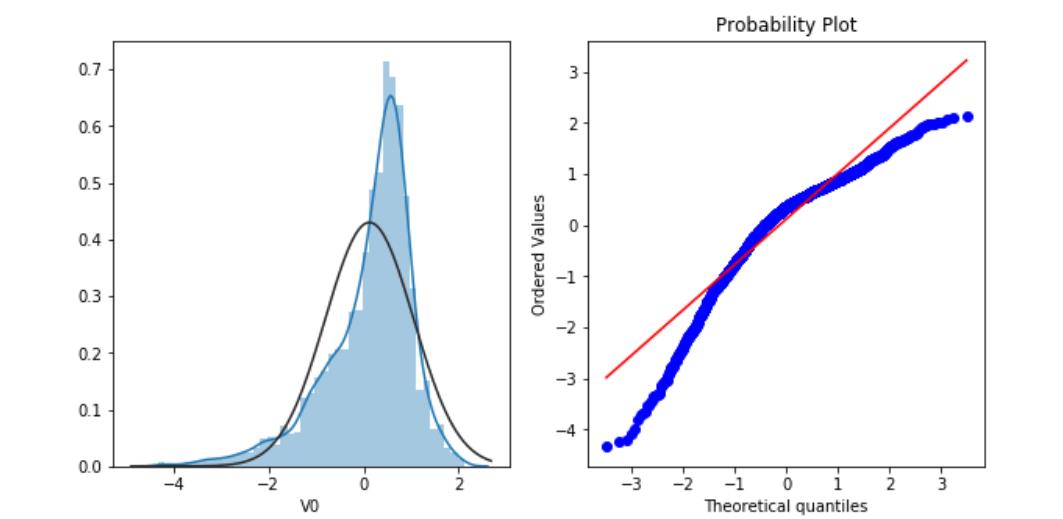
直方图是用来描述数据的分布形状，QQ图可以判断数据分布是否属于正态分布。

#直方图和QQ图
#QQ图是指数据的分位数和正态分布的分位数对比参照的图，如果数据符合正态分布，所有的点都会落在直线上。
#我们首先绘制V0变量的统计分布
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
sns.distplot(train_data["V0"],fit=stats.norm)#fit=stats.norm代表标准正态分布
plt.subplot(1,2,2)
stats.probplot(train_data["V0"],plot=plt)

结果如下：

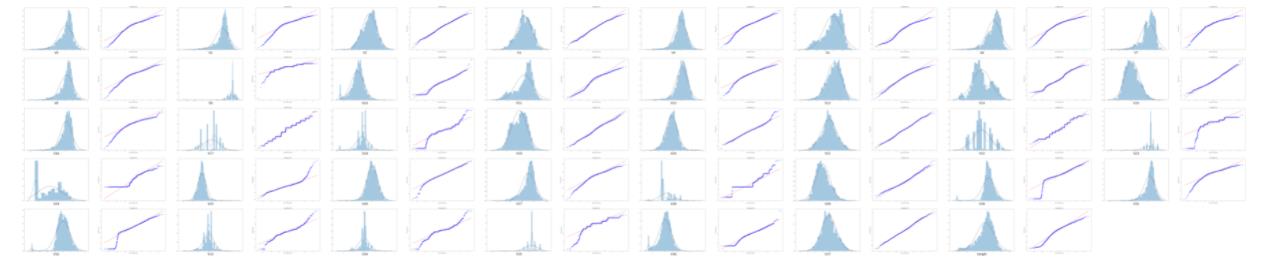
将所有的变量都判断一下：

#画出所有函数的直方图和QQ图
plt.figure(figsize=(256,128))
i=0 
for col in column:
    i+=1
    plt.subplot(6*2,8*2,i)
    sns.distplot(train_data[col],fit=stats.norm)
    plt.xlabel(col,fontsize=36)
    
    i+=1
    plt.subplot(6*2,8*2,i)
    stats.probplot(train_data[col],plot=plt)
plt.show()

5.训练集和测试集的分布

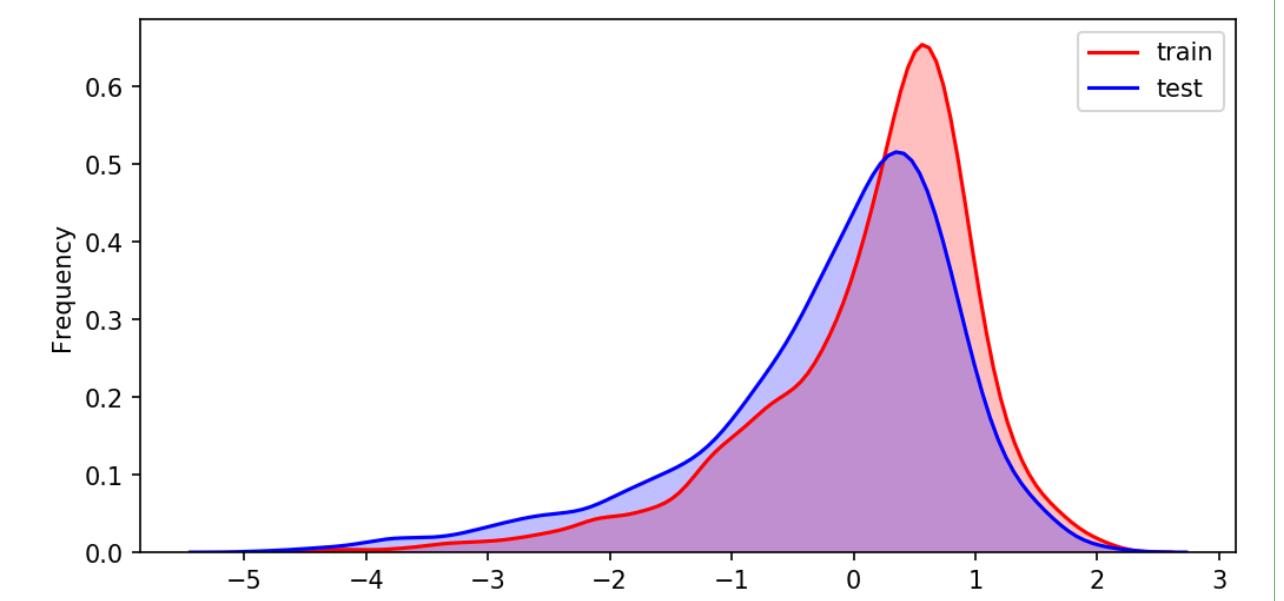
训练集和测试集分布不一致会影响模型训练的结果。我们可以使用KDE的方法来判断训练集和测试集来判断是否属于一个分布。

#KDE分布图
#核密度估计，可以理解为是对直方图的加窗平滑，通过绘制KDE分布图，可以查看并对比训练集和测试级中特征变量的分布情况，发现两个数据集中分布不一致的情况！
plt.figure(figsize=(8,4),dpi=150)
ax=sns.kdeplot(train_data["V0"],color="Red",shade=True)
ax=sns.kdeplot(test_data["V0"],color="blue",shade=True)
ax.set_xlabel("V0")
ax.set_ylabel("Frequency")
ax=ax.legend(["train","test"])
plt.show()

结果如下：

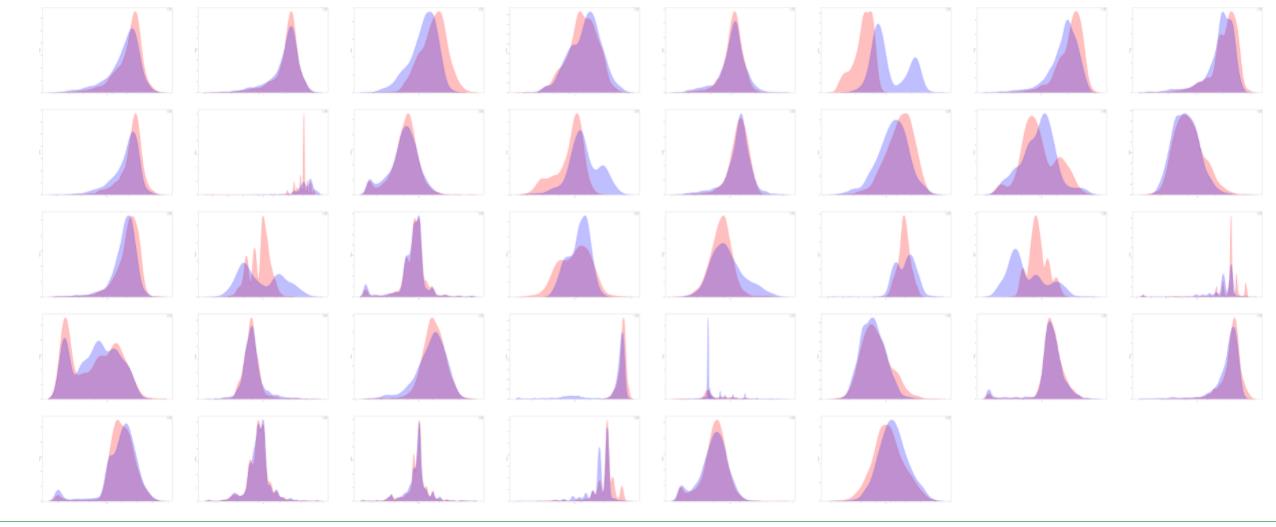
将多个表都画出来

#画出所有函数的kde图，需要注意的是测试集没有target标签！所以target不要做kde
plt.figure(figsize=(256,128))
for i in range(len(column)-1):
    ax=plt.subplot(6,8,i+1)
    ax=sns.kdeplot(train_data[column[i]],color="Red",shade=True)
    ax=sns.kdeplot(test_data[column[i]],color="blue",shade=True)
    ax.set_xlabel(column[i])
    ax.set_ylabel("Frequency")
    ax=ax.legend(["train","test"])
plt.show()

结果如下：

6.判断线性相关

这里我们画出了一个特征与目标分布的图像。

#主要是分析变量之间的线性回归关系
plt.figure(figsize=(8,4),dpi=150)
ax=plt.subplot(1,2,1)
sns.regplot(x="V0",y="target",data=train_data,ax=ax,scatter_kws={'marker':'.','s':3,'alpha':0.3},line_kws={'color':'r'});
plt.xlabel('V0')
plt.ylabel('target')
ax=plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')
plt.show()

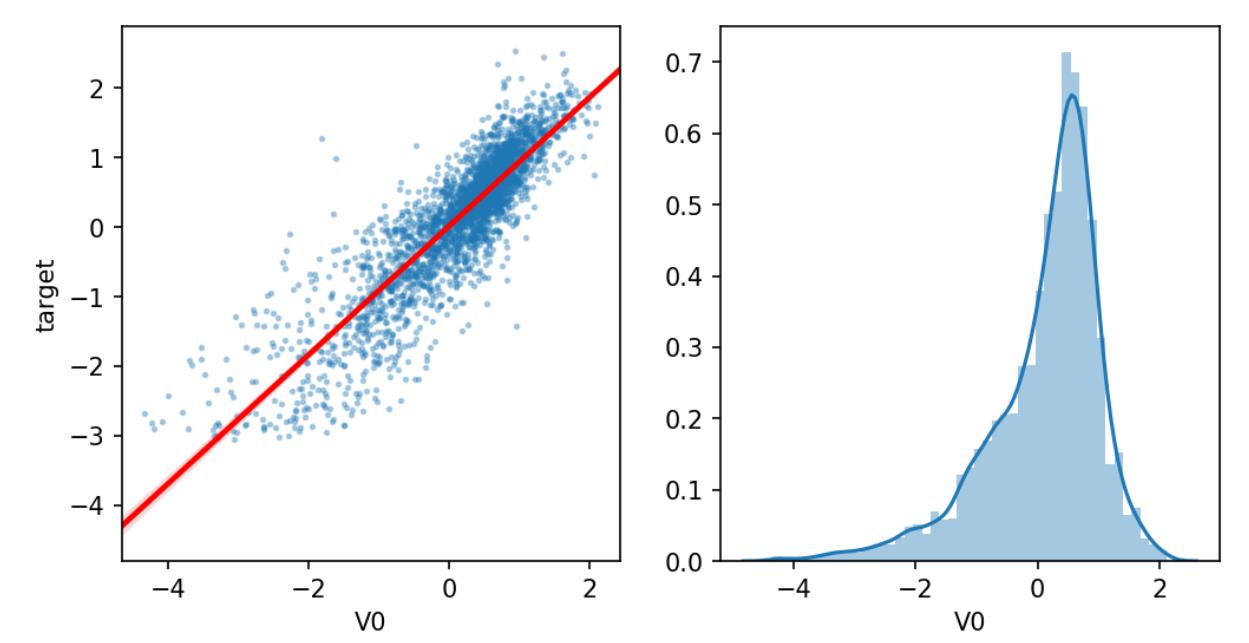
画出所有的图像

#画出所有的变量与目标值之间的线性关系
plt.figure(figsize=(256,128))
i=0
for col in test_data.columns:
    i+=1
    ax=plt.subplot(2*6,2*8,i)
    sns.regplot(x=col,y="target",data=train_data,ax=ax,scatter_kws={'marker':'.','s':3,'alpha':0.3},line_kws={'color':'r'});
    plt.xlabel(col)
    plt.ylabel('target')
    i+=1
    ax=plt.subplot(2*6,2*8,i)
    sns.distplot(train_data[col].dropna())
    plt.xlabel(col)
    plt.show()
    

7.变量的相关性

#变量之间的相关关系进行分析可以为后面特征工程做准备
#这里我们删除了训练集和测试集分布不一样的特征
pd.set_option('display.max_columns',10)
pd.set_option('display.max_rows',10)
data_train1=train_data.drop(['V5','V9','V11','V17','V22','V28'],axis=1)
train_corr=data_train1.corr()#计算相关系数
train_corr

展示一个相关系数矩阵：

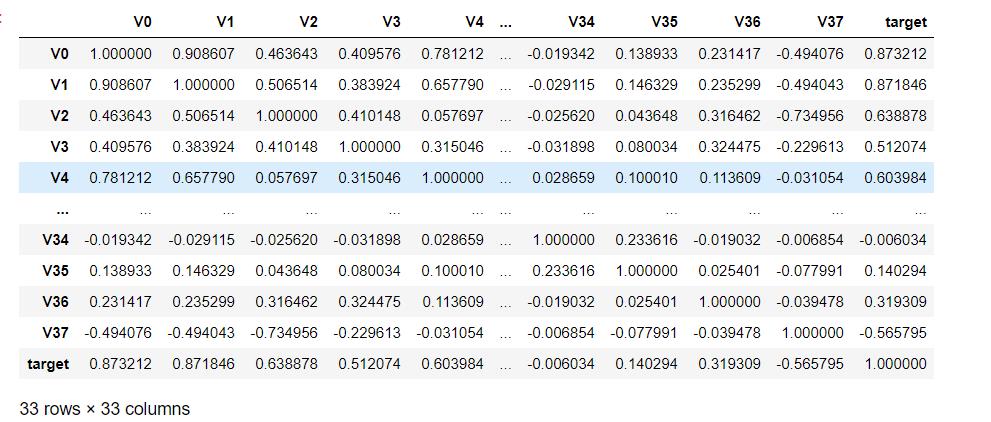
画出热力图

#画出热力图
ax=plt.subplots(figsize=(20,16))#调整画布的大小
ax=sns.heatmap(train_corr,vmax=8,square=True,annot=True)#热力图

结果如下：

筛选出较高的相关特征

#根据相关系数来筛选特征变量
#找寻K个特征与目标值最相关
k=10
cols=train_corr.nlargest(k,'target')['target'].index
print("cols.index",cols)
cm=np.corrcoef(train_data[cols].values.T)
plt.figure(figsize=(10,10))
hm=sns.heatmap(train_data[cols].corr(),square=True,annot=True)
cm

部分数据展示如下：

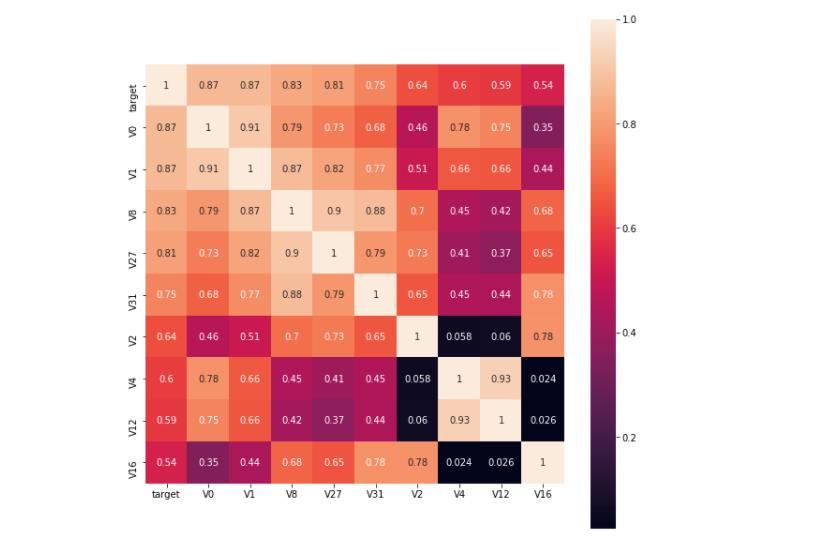
找出相关系数大于0.5的特征

#找出相关系数大于0.5的特征
threshold=0.5
corrmat=train_data.corr()
top_corr_features=corrmat.index[abs(corrmat["target"])>threshold]
plt.figure(figsize=(10,10))
g=sns.heatmap(train_data[top_corr_features].corr(),cmap="RdYlGn",annot=True)

这里需要说明一下，相关系数只与绝对值的大小有关，一般用绝对值的大小来判断相关性。

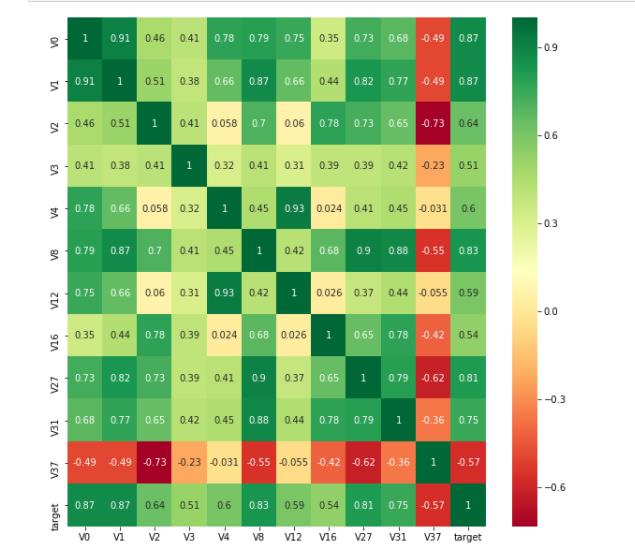
去除相关性较小的特征
对于相关性较小的特征，我们可以去除。

# threshold=0.5
#相关系数矩阵
corr_matrix= data_train1.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index
data_all.drop(drop_col,axis=1,inplace=True)

8.Box-Cox变换

Box-Cox变化是统计建模中一种常用的建模方法，主要是用于在连续的响应变量不满足正态分布时，可以采用Box-Cox变换，使线性回归模型在满足线性、正态性、独立性及方差齐性的同时又不丢失信息。但在Box-Cox变换之前，需要对数据进行归一化！

#box-cox变换！将数据转换为满足正态分布的数据
#Box-cox变换是统计建模中常用的一种数据转换的方式。在联系的响应变量不满足正态分布是可以使用该变化，这一变换可以使线性回归模型在满足线性、正态性、独立性及方差齐性的同时，又不丢失信息。
#变换之前需要做归一化
drop_columns=['V5','V9','V11',"V17","V22","V28"]#删除分布不均的数据
train_x=train_data.drop(['target'],axis=1)
#data_all=pd.concat([train_data,test_data],axis=0,ignore_index=True)
data_all=pd.concat([train_x,test_data])
data_all.drop(drop_columns,axis=1,inplace=True)
data_all.head()

关于数据的归一化处理，我们有以下几点需要注意;

• 可以将训练集和测试集合并之后一起做归一化。
• 可以分开对数据进行归一化处理。不过前提是测试集和训练数据分布一致。

合并归一化

#合并之后进行归一化
cols_numeric=list(data_all.columns)
def scale_data(col):
    return (col-col.min())/(col.max()-col.min())
data_all[cols_numeric]=data_all[cols_numeric].apply(scale_data,axis=0)
data_all[cols_numeric].describe()`

分开归一化

#数据分开归一化
train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_data,axis=0)

test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_data,axis=0)

Box-Cox变换

#我们这里是对训练集和测试集一起归一化，也可以分开进行归一化，（分开）这种方式需要建立训练数据和测试数据分布一直的情况下，建议在数据量大的情况下使用。
# 绘图显示Box-Cox变换对数据分布影响
cols_numeric_left = cols_numeric[0:13]
cols_numeric_right = cols_numeric[13:] #这里是将特征分为两部分，前13个为第一部分
## Check effect of Box-Cox transforms on distributions of continuous variables

train_data_process = pd.concat([train_data_process, train_data['target']], axis=1)

fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4*fcols,4*frows))
i=0
for var in cols_numeric_left:
    dat = train_data_process[[var, 'target']].dropna()
        
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(dat[var] , fit=stats.norm);
    plt.title(var+' Original')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(dat[var], plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var]))) #计算数据集的偏度
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(dat[var],dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var],dat['target'])[0][1]))
 
    i+=1
    plt.subplot(frows,fcols,i)
    trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
    trans_var = scale_data(trans_var)    
    sns.distplot(trans_var , fit=stats.norm);
    plt.title(var+' Tramsformed')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(trans_var, plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var))) #归一化后，偏度明显变小，相关性变化不大
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_var, dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))

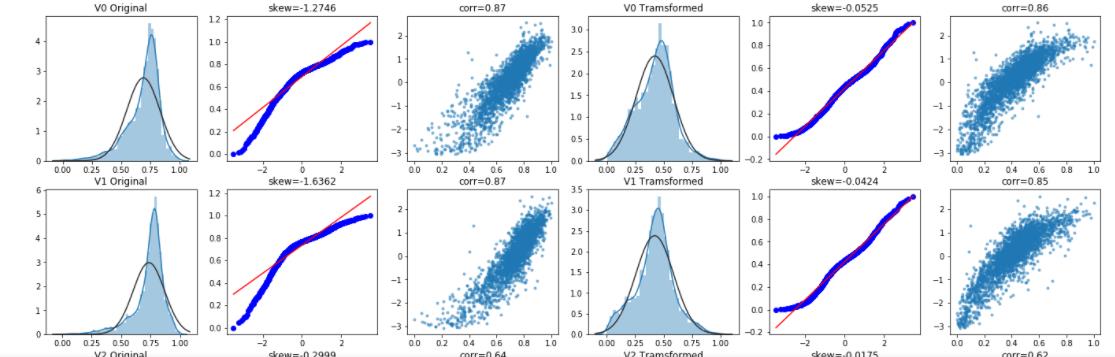
做完这些，你对数据就有了大致的了解，接下来就可以做特征工程了！