替换法（代入法）求解递归式

Posted 2021-06-26 桃陉

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了替换法（代入法）求解递归式相关的知识，希望对你有一定的参考价值。

一.原理

替换法（或者叫代入法）就是我们直接对T(n)进行猜测，然后带入原递归式中进行验证。也就是猜测一个界，然后使用数学归纳法来证明这个界是对的。

${\\color{Red}步骤}$ :

(1)猜测解的形式

(2)使用数学归纳法求出解中的常数，并证明解是正确的。

${\\color{Blue}猜测要靠经验，偶尔还要靠创造力}$

现在有递归式如下：

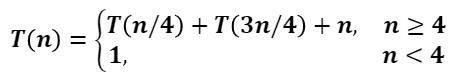
在这里插入图片描述
我们首先对其进行猜测（这个最终结果算的好不好就看你猜的准不准了，有点玄学）：
$\\theta(nlogn)$
然后进行求解（在这里因为该式有两个区间，分别有不同的取值，所以我们使用数学归纳法）：

当 n = 3 时：有 $c_{1}*3log3≤1≤c_{2}*3log3$ 解得 ${\\color{Red} 0<c_{1}\\le \\frac{1}{3log3},c_{2}\\ge\\frac{1}{3log3}}$

当小于n时：假设命题成立

当等于n时：带入可得 $T(\\frac{n}{4}) + T(\\frac{3n}{4}) + n \\le c_{2}*\\frac{n}{4}*log\\frac{n}{4} + c_{2}*\\frac{3n}{4}*log\\frac{3n}{4} + n$

对等式右边化简： $（c_{2}*\\frac{n}{4}*（logn-log4))+(c_{2}*\\frac{3n}{4}*(logn-log\\frac{4}{3}))+n$

展开合并得： $c_{2}nlogn-(c_{2}n(log4-\\frac{3}{4}log3))+n$

将后面的n提取出来可得： $c_{2}nlogn-(c_{2}(log4-\\frac{3}{4}log3)-1)n$

根据定义，需要使等式右边即上式 ≤ c₂nlogn

所以只需要让 $(c_{2}(log4-\\frac{3}{4}log3)-1)n \\ge 0$

解得： ${\\color{Red} c_{2} \\ge \\frac{1}{log4-\\frac{3}{4}log3} >0}$

若想使 $T(n)≤c_{2}nlogn$
只需取他们中较大的值： ${\\color{Red} c_{2} \\ge max( \\frac{1}{log4-\\frac{3}{4}}log3,\\frac{1}{3log3} )}$

此时不等式右边的约束条件的参数c₂就取到了，同理我们可以解得不等式右边的约束变量c₁的取值：
${\\color{Red} 0<c_{1}\\le min(\\frac{1}{log4-\\frac{3}{4}log3},\\frac{1}{3log3})}$