要想学好八大排序算法这篇文章你不得不看,巨详细王大爷表示都看得懂
Posted 程序猿是小贺
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了要想学好八大排序算法这篇文章你不得不看,巨详细王大爷表示都看得懂相关的知识,希望对你有一定的参考价值。
今天是6月8号高考第二天,先祝考生们金榜题名哈,接着进入正题…

C语言版八大排序算法
1.插入排序
插入排序,一般也被称为直接插入排序。
1.1基本思想
插入排序是指在待排序的元素中,假设前面n-1 (其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。. 按照此法对所有元素进行插入,直到整个序列排为有序的过程,称为插入排序。
1.2动图演示
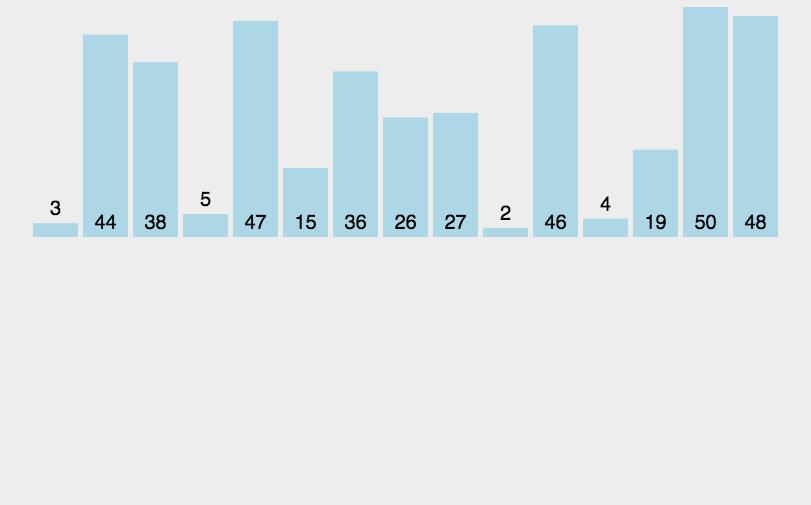
静态图解
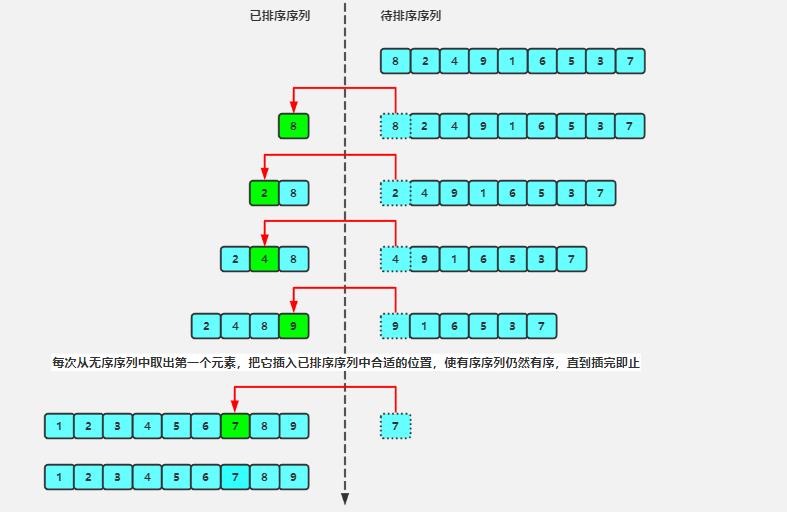
1.3代码实现
//插入排序
void InsertSort(int arr[], int size)
{
//表示当前要插入元素在数组中的下标
//并且此时i位置的元素一定是要往i之前的位置插入
for (int i = 1; i < size; i++)
{
//在i之前找插入的位置,因为此时i之前的位置是有序的
int end = i - 1;
int key = arr[i];
while (end >= 0 && key < arr[end])
{
arr[end + 1] = arr[end];
end--;
}
//判断并插入元素
arr[end + 1] = key;
}
}
1.4插入排序特性:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
判断稳定性方法:如果排序后两个相同的数的相对顺序不会发生改变,则该算法是稳定的;如果排序后,数据的相对次序发生了变化,则该算法是不稳定的。
2.希尔(Shell)排序
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。
2.1基本思想
该方法实质上是一种分组插入方法。比较相隔较远距离(称为增量)的数,使得数移动时能跨过多个元素,则进行一次比较就可能消除多个元素交换。算法先将要排序的一组数按某个增量gap分成若干组,每组中记录的下标相差gap对每组中全部元素进行排序,然后再用一个较小的增量对它进行分组,在每组中再进行排序。当增量减到1时,整个要排序的数被分成一组,排序完成。
一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
补充:希尔排序的性能依赖于增量序列的选择,源于这点许多大佬给出了很多不同的方法,有位大佬通过大量的实验,给出了较好的结果gap=gap/3+1这一方法时,算法比较和移动的次数约在n(1.25)到(1.6n)1.25之间
2.2动图演示
此处采用的是gap/=2,大家参考
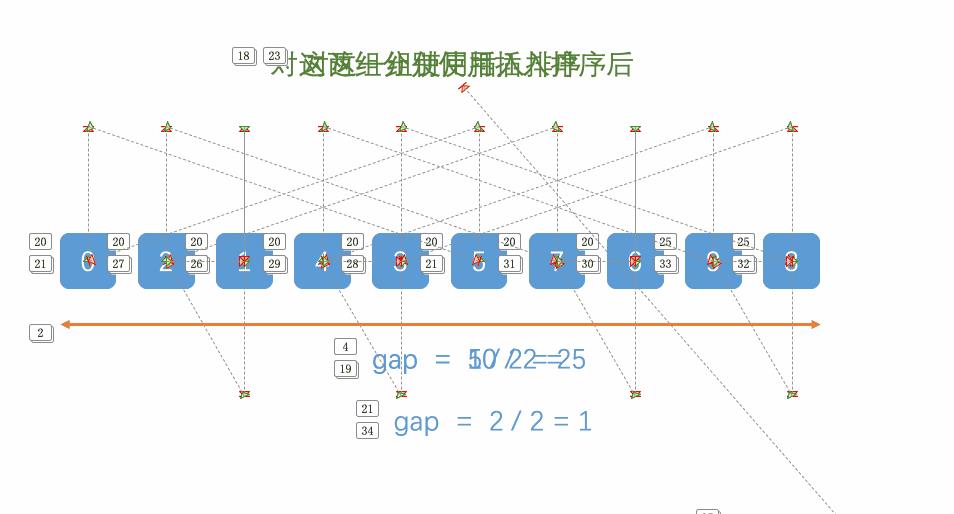
静态图解
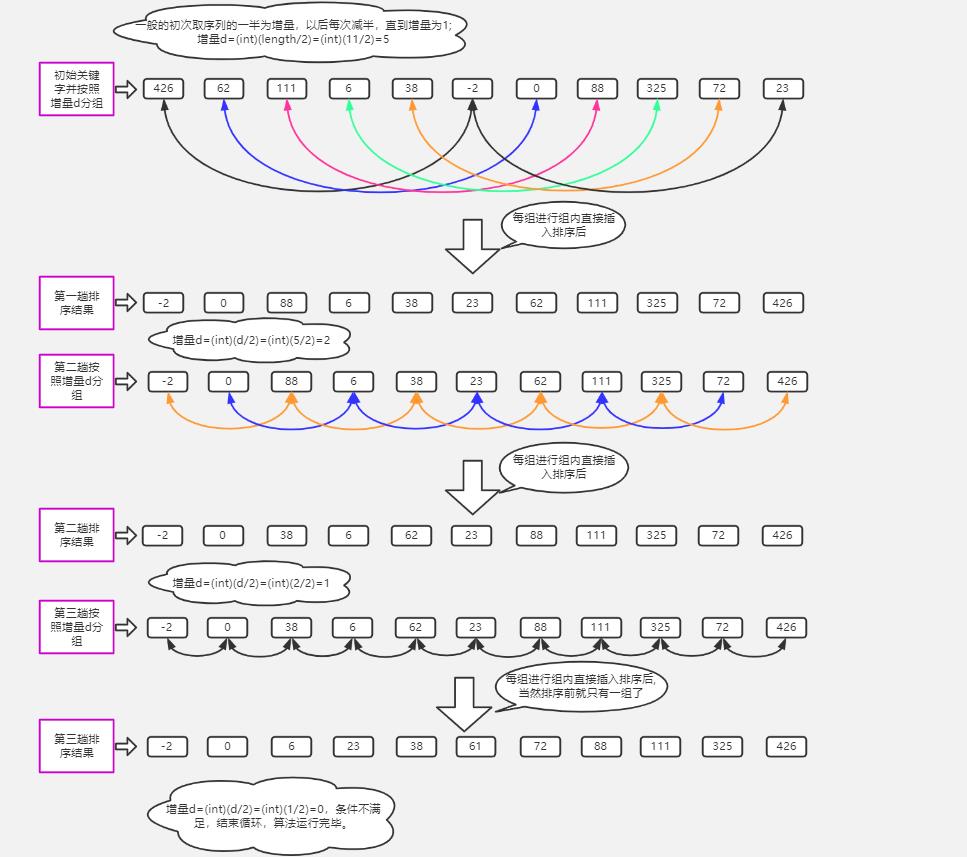
2.3代码实现
//希尔排序
void ShellSort(int arr[], int size)
{
int gap = size ;
//gap最小值为1,循环条件必须大于1
while (gap >1)
{
gap = gap / 3 + 1;//Knuth大佬提出的取值方式
//下面类似插入排序,只是此时插入时要间隔gap个元素进行插入
//i的取值可以按顺序往下取,按顺序插入
//取元素的时候不需要间隔gap个,不然还需在外面加一重循环
for (int i = gap; i < size; i++)
{
int end = i - gap;
int key = arr[i];
while (end >= 0 && key < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
arr[end + gap] = key;
}
}
}
2.4希尔排序特性
- 希尔排序是对直接插入排序的进一步优化。
- 希尔排序的时间复杂度不好计算,平均时间复杂度: O(N1.3~N2)
- 稳定性:不稳定
- 针对元素数据比较大,杂乱的场景
3.选择排序
选择排序(Selection sort)是一种简单直观的排序算法。
3.1基本思想
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
3.2动图演示
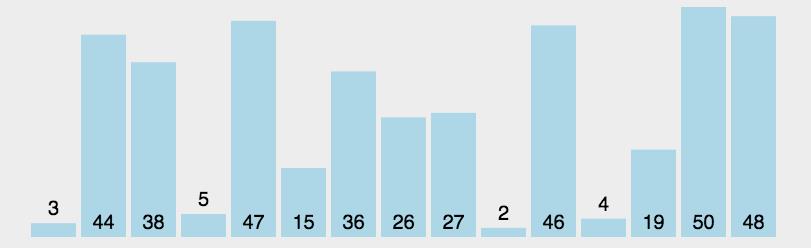
静态图解
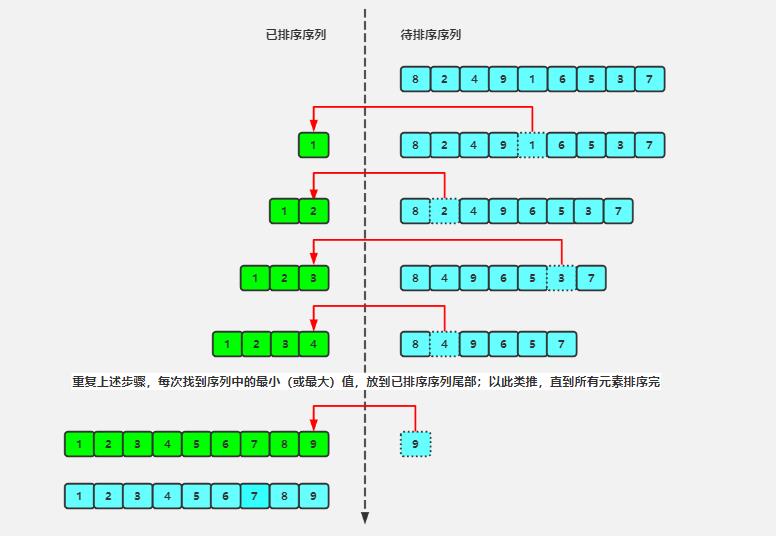
3.3代码实现
//交换函数
void Swap(int *left, int *right)
{
int tmp = *left;
*left = *right;
*right = tmp;
}
//选择排序
//法一:找到数组中元素最大元素的位置,与数组末尾元素交换,交换完毕size减一
//重复以上步骤,直至size=1
void SelectSort(int arr[], int size)
{
while (size >1)
{
int max = 0;
//在数组中找出最大元素的位置,然后标记
for (int i = 1; i < size; i++)
{
if (arr[i] > arr[max])
{
max = i;
}
}
//此时如果max没有在数组末尾,则将max与数组中最后一个元素交换位置
if (max != size - 1)
{
Swap(&arr[max], &arr[size - 1]);
}
//size减一,减去已经拍好的那个最大值的位置,其他位置还是无序的,则循环继续
//当size等于一时,表示此时数组中只有一个元素,循环结束
size--;
}
}
方法改进思路:
我们既然可以找其最大或者最小的位置,那么我能不能同时找最大和最小的位置。这样可以一次找出最大最小两个值,效率更高。
改进代码实现
//方法二:同时找出数组中最大和最小元素的位置,
//循环将i所在位置的元素分别与max,min位置所在的元素进行比较,
//如果该元素大于max所在位置的元素则让max标记该元素
//如果该元素小于民所在位置元素则让min标记该元素
//(注意:此时要先判断min是否在end位置,如果在则将max赋给min)
//此时若max不在end位置,则将max位置的元素与end位置的元素交换
//此时若min不在begin位置,则将min位置的元素与begin位置的元素交换
void SelectSort2(int arr[], int size)
{
int begin = 0;
int end = size - 1;
//从两端往中间循环,相遇则循环结束
while (begin < end)
{
int max = begin;
int min = begin;
for (int i = 1; i <= end;i++)
{
if (arr[i]>arr[max])
{
max = i;
}
if (arr[i] < arr[min])
{
min = i;
}
}
if (min == end)
{
min = max;
}
if (max!= end)
{
Swap(&arr[max], &arr[end]);
}
if (min != begin)
{
Swap(&arr[min], &arr[begin]);
}
//两端元素排好,中间还是无序,数组缩短往中间靠
begin++;
end--;
}
}
3.4选择排序的特性
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
3.5选择排序的缺陷
存在大量的重复比较,优化----堆排序
4.堆排序
堆排序(Heapsort)是指利用堆这一数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
4.1基本思想
略…
4.2静态图解
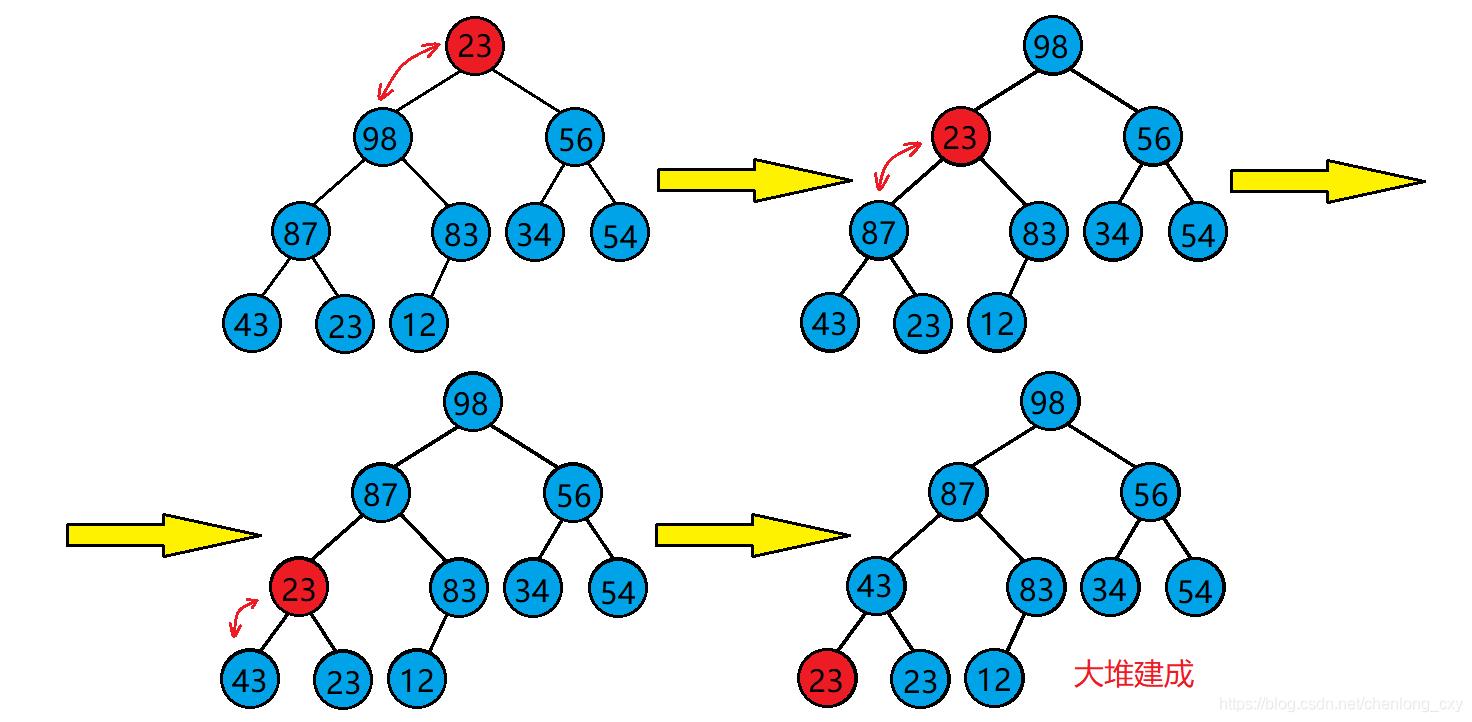
4.3代码实现
在我数据结构C语言 《四》二叉树,堆的基本概念以及堆的相关操作实现(上)这一文中有关于堆排序代码实现这里也就不做详细解释了。
4.4堆排序的特性:
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
5.冒泡排序
算法名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
5.1基本思想
1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2.对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
3.针对所有的元素重复以上的步骤,除了最后一个。
4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
5.2动图演示
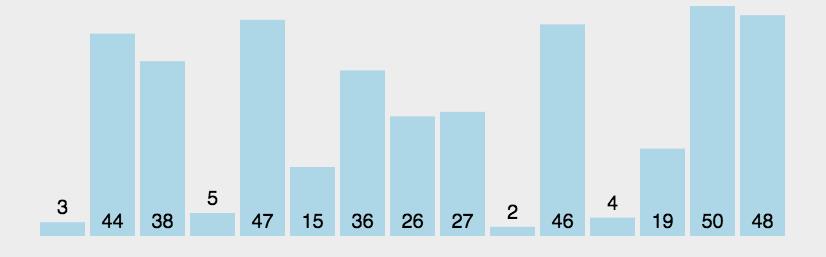
静态图解
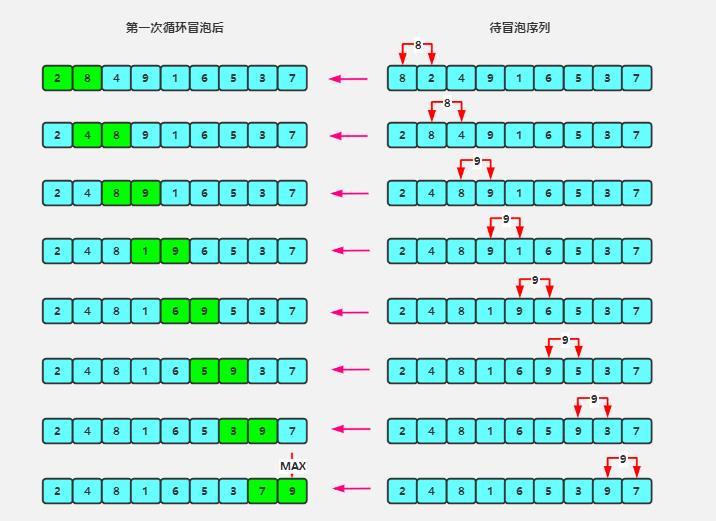
5.3代码实现
//冒泡排序
void BubbleSort(int arr[], int size)
{
//此层循环控制冒泡的趟数,最后一趟时只剩一个元素,不用比较
for (int i = 0; i < size - 1; i++)
{
//定义一个标志位,表示这一趟期间有没有发生交换
int flag = 0;
//冒泡方式:相邻两个元素比较,不满足则交换
for (int j = 0; j < size - i - 1; j++)
{
if (arr[j]>arr[j + 1])
{
flag = 1;//有交换将flag赋值为1
Swap(&arr[j], &arr[j + 1]);
}
}
//判断此时flag 的值,若为0表示没有交换说明数组已经有序,则直接退出
if (flag == 0)
return;
}
}
5.4冒泡排序特性
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:稳定
6.快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法。
6.1递归方法
基本思想
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
实现代码
void QuickSort(int arr[], int left,int right)
{
//当数组中数据小于两个时,不用交换
if (right - left < 2)
return;
else
{
//按基准值div来对区间进行划分
int div = Divide(arr, left, right);//hoare法
//int div = Fill(arr, left, right);//填坑法
//int div = Point(arr, left, right);//前后指针法
//递归排左边部分
QuickSort(arr, left, div);
//递归排右边部分
QuickSort(arr, div + 1, right);
}
}
6.2.1Hoare方法
基本思想
见代码段…
动图演示
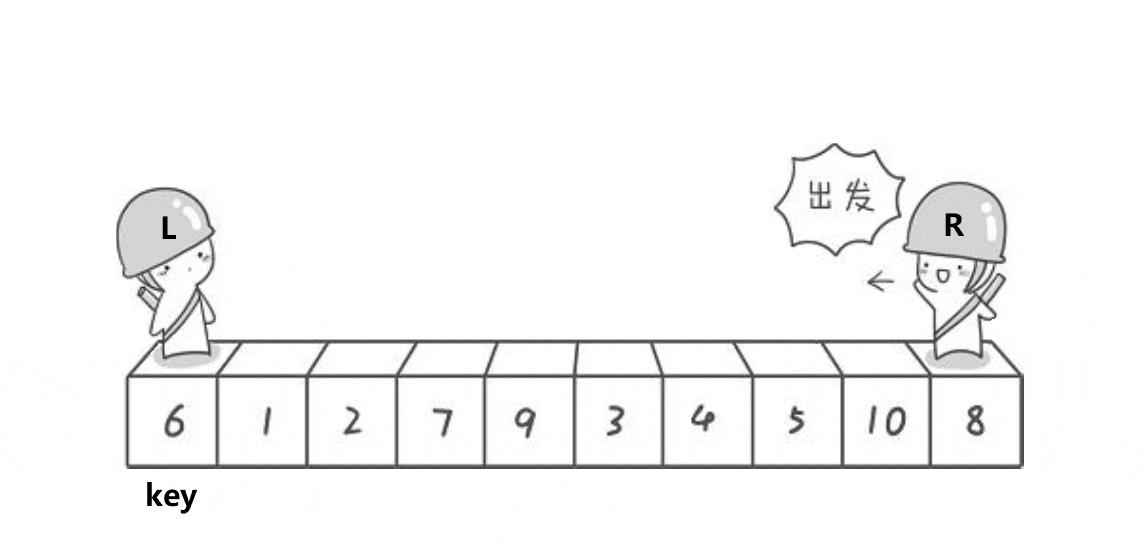
实现代码
//方法一:hoare版本
int Divide(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
int key = arr[end];
while (begin < end)
{
//让 begin从前往后找,找到比基准值大的数则停下
while (begin < end && arr[begin] <= key)
{
begin++;
}
//让end从后往前找,找到比基准值小的数停下
while (begin < end && arr[end] >= key)
{
end--;
}
if (begin < end)
{
//将begin的位置与end位置的数据交换
Swap(&arr[begin], &arr[end]);
}
}
if (begin != right-1)
{
//将此时begin或者end的位置的数据与最后一个位置的数据交换
Swap(&arr[begin], &arr[right-1]);
}
return begin;
}
6.2.2填坑法
动图演示
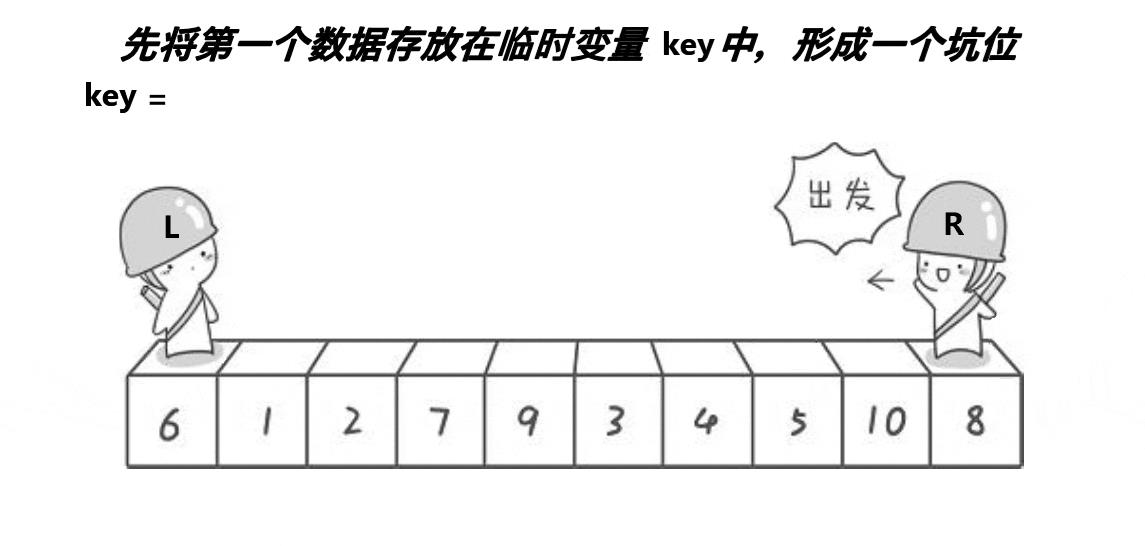
代码实现
int Fill(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
int key = arr[end];//把末尾的值放在key位置,此时end位置是个坑
while (begin < end)
{
//让begin往后走,找到比基准值小的数停下
while (begin < end && key >= arr[begin])
{
begin++;
}
//将此时位置的值填在end位置,此位置出现新的坑
if (begin < end)
{
arr[end] = arr[begin];
end--;
}
//让end从后往前找,找到比基准值小的数停下
while (begin < end && key <= arr[end])
{
end--;
}
//将此时位置的值填在begin位置,此位置出现新的坑
if (begin < end)
{
arr[begin] = arr[end];
begin++;
}
}
//用key位置的值将这个位置的坑填上
arr[begin] = key;
return begin;
}
6.2.3前后指针法
动图演示

实现代码
//前后指针法
int Point(int arr[], int left, int right)
{
int cur = left;
int prev = cur - 1;
int key = arr[right - 1];
//cur从前往后走
while (cur < right)
{
//将比基数值大的数往后放,比基数值小的数往前放
//如果此时cue的值小于基数值并且prev走一步不等于cur,则交换
if (arr[cur] < key && prev++ != cur)
{
Swap(&arr[prev], &arr[cur]);
}
//cur往后走
cur++;
}
//最后把基数值的位置的数与prev的下一个位置的数交换
if (++prev != right - 1)
{
Swap(&arr[prev], &arr[right - 1]);
}
return prev;
}
我们不能保证每次选取的key都是值正中间的那个数,如果基准值取得比较好,则每次都可以划分为在左右均等的两部分,如果序列有序或者接近有序,快排的性能会非常差,结构就会从平衡二叉树转变为单支树。
6.2.4快排优化
尽量避免取到max值或min值,可以使用三数取中法来实现。
三数取中法基本思想
从左侧,中间,右侧各取一个值,比较其大小,取其值大小位于中间的那个树作为基准值。
代码实现
int GitMid(int arr[], int left, int right)
{
//mid等于左侧加上右侧除以2,
int mid = (left + (right - left)) / 2;
//左比右小
if (arr[left] < arr[right - 1])
{
//左比右小且左大于中间,返回最左侧的那个值
if (arr[left] > arr[mid])
{
return left;
}
//左比右小但中间那个比右大,返回右侧的那个值
else if (arr[mid]>arr[right - 1])
{
return right - 1;
}
else
{
return mid;
}
}
//与上面比较方法一致
else
{
if (arr[right - 1] > arr[mid])
return right - 1;
else if (arr[mid] > arr[left])
return left;
else
return mid;
}
}
优化后以Hoare方法为例,其余方法与其类似,所以在此只实现一种参考。
代码实现
int Divide(int arr[], int left, int right)
{
int begin = left;
int end = right - 1;
//找到三数取中法取到的中间值,即为基准值
int mid = GitMid(arr, left, right);
//将该值与末尾值交换
Swap(&arr[mid], &arr[right-1]);
int key = arr[right-1];
while (begin < end)
{
//让 begin从前往后找,找到比基准值大的数则停下
while (begin < end && arr[begin] <= key)
{
begin++;
}
//让end从后往前找,找到比基准值小的数停下
while (begin < end && arr[end] >= key)
{
end--;
}
if (begin < end)
{
//将begin的位置与end位置的数据交换
Swap(&arr[begin], &arr[end]);
}
}
if (begin != right-1)
{
//将此时begin或者end的位置的数据与最后一个位置的数据交换
Swap(&arr[begin], &arr[right-1]);
}
return begin;
}
再次进行优化,如果数据量比较小或者接近有序的时候,最优的方法应该是插入排序,则可设置一个临界条件,将代码再次优化如下,后面与上述实现方式相同
if (right - left <= 一个临界值)
{
InsertSort(arr + left, right-left);
}
快排分析:
快速排序基本上被认为是相同数量级的所有排序算法中,平均性能最好的。快速排序是在冒泡排序的基础上改进而来的,冒泡排序每次只能交换相邻的两个元素,而快速排序是跳跃式的交换,交换的距离很大,因此总的比较和交换次数少了很多,速度也快了不少。
6.2非递归方法
借助栈实现
关于栈的创建初始化在我之前的文章数据结构C语言篇《三》栈和队列概念,模拟函数实现,以及相关OJ面试题文中已经实现过,有问题的小伙伴可以去看看,我这里就不过多赘述了。
实现代码
void QuickSortNor(int arr[], int size)
{
Stack s;
StackInit(&s);
int left = 0;
int right = size;
//压栈
StackPush(&s, left);
StackPush(&s, right);
while (!StackEmpty(&s))
{
//根据栈的特性只能先取右边并出栈再取左边
right = StackTop(&s);
StackPop(&s);
left = StackTop(&s);
StackPop(&s);
if (right - left > 1)
{
//用上述三种方法任意之一即可
int div = Divide(arr, left, right);
//此时要想先取左半侧在取右半侧,则需根据栈的特性先要将右半侧压栈再将左半侧压栈
StackPush(&s以上是关于要想学好八大排序算法这篇文章你不得不看,巨详细王大爷表示都看得懂的主要内容,如果未能解决你的问题,请参考以下文章