监督学习方法解决时序预测问题
Posted zhuo木鸟
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了监督学习方法解决时序预测问题相关的知识,希望对你有一定的参考价值。
文章目录
内容概述
请务必阅读
本文主要结合 EUNITE 技术交流协会举办的一次公益比赛, 讲解时序预测问题的监督学习解决办法。
文章重点在于理论细节,而非解题的代码展示。
本人专挑数据挖掘、机器学习和 NLP 类型的题目做,有兴趣也可以逛逛我的数据挖掘竞赛专栏。
如果本篇博文对您有所帮助,请不要吝啬您的点赞 😊
赛题描述
比赛就一题:根据斯洛伐克东部电力公司,于 1997-1998 年的电力负荷数据、是否公开节假日数据、当天的温度数据,预测 1999 年 1 月的电力负荷数据。
比赛给出的数据采样频率是半小时,为了方便处理,本文对其进行求和,从而根据一天的电力负荷来解决问题。
数据如下:
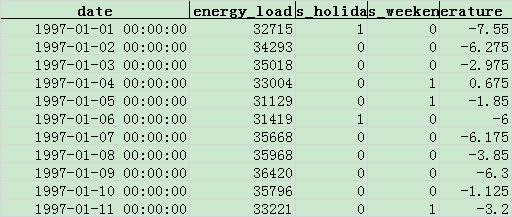
1997 年:(最后一列是 Temperature,温度列,下同)
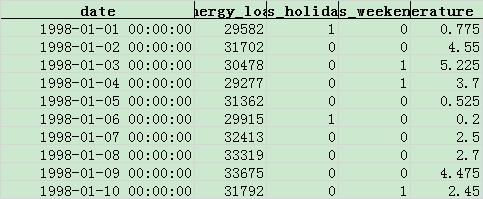
1998 年:
1999 年:(倒数第二列是 Temperature,温度列,下同)
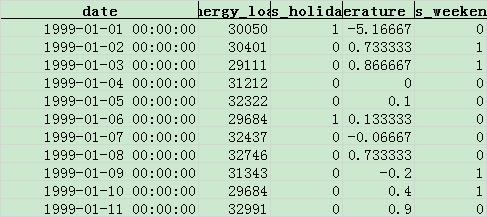
我们将使用 1997-1998 年的数据,训练一个时序预测模型,并预测 1999 年 1 月每天的负荷数据,并用 1999 年的实际负荷数据,评价模型的效果。
数据描述
在进行时序预测之前,有必要对数据进行分析,我们可以采取如下方法:
- 计算数据的统计描述(均值、方差、四分位数等)
- 画出预测目标,随时间的变化(若有条件,可以配上其他信息)
- 画出预测目标的频率分布直方图
- 画出预测目标的自相关图
数据统计描述
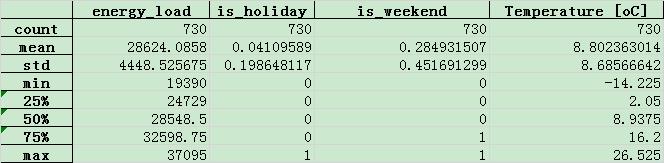
虽然得出数据的总体的统计描述,只是对数据进行了一个大致的“瞭望”。在很多情况下,实际数据可不是这么风平浪静,特别是方差,有时会波动很大。
另外,我们也可以“分段”地计算数据的统计描述(summary time series every specific period)。并对比每一段的统计量,比如均值,或可以掌握数据随时间的一些变化趋势。
画线图(散点图)
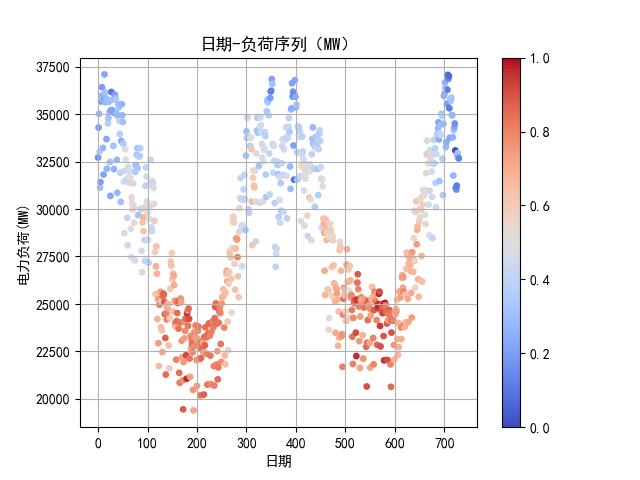
如下图所示,我们绘制负荷预测,和日期的变化数据,同时根据当天的温度,标注散点颜色。
不看散点的颜色,可以看到负荷序列是有一个“周期的”。
结合温度信息,可以看到,温度越低,负荷越高。
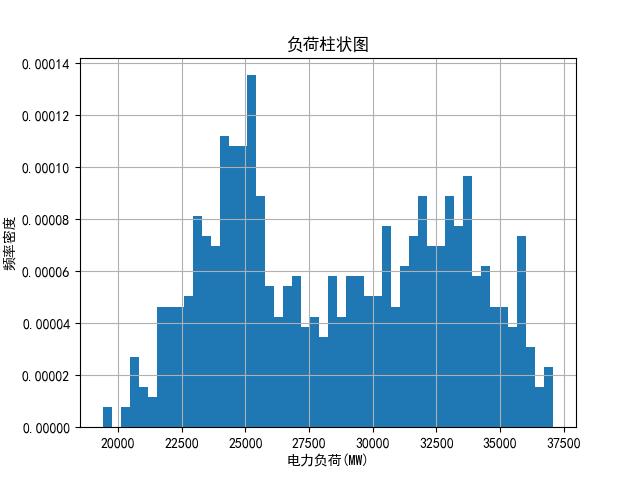
频率密度直方图
画出频率密度直方图,频率密度的值根据下式计算:
y
=
c
o
u
n
t
s
u
m
(
c
o
u
n
t
)
⋅
b
i
n
_
w
i
d
t
h
y = \\frac{count}{sum(count)\\cdot bin\\_width}
y=sum(count)⋅bin_widthcount
其中 bin_width 是 x 轴一块的宽度。
自相关图
画出自相关图如下:
其中,x 轴是时间延迟,记为 k k k。若当前数据为 x ( t ) x(t) x(t),则时间延迟 k k k 的数据为 x ( t − k ) x(t-k) x(t−k)。
自相关系数即为:
x
(
t
)
x(t)
x(t) 和
x
(
t
−
k
)
x(t-k)
x(t−k) 的 Pearson 相关系数:
r
=
∑
(
x
t
−
x
ˉ
t
)
∑
(
x
t
−
k
−
x
ˉ
t
−
k
)
∑
(
x
t
−
x
ˉ
t
)
2
×
∑
(
x
t
−
k
−
x
ˉ
t
−
k
)
2
r = \\frac{\\sum(x_t-\\bar{x}_t) \\sum(x_{t-k}-\\bar{x}_{t-k})} {\\sqrt{\\sum(x_t-\\bar{x}_t)^2} \\times \\sqrt{\\sum(x_{t-k}-\\bar{x}_{t-k})^2}}
r=∑(xt−xˉt)2×∑(xt−k−xˉt−k)2∑(xt−xˉt)∑(xt−k−xˉt−k)
换句话说,自相关系数本质是 Pearson 相关系数。若数据的分布不是正态分布,则 Pearson 相关系数表示数据的线性相关性。
因此,我们可以看到,当 k = 1 k=1 k=1 时,数据的自相关性接近于 1。换句话说,当前数据,和上一个时间的数据,存在着较强的线性相关性。
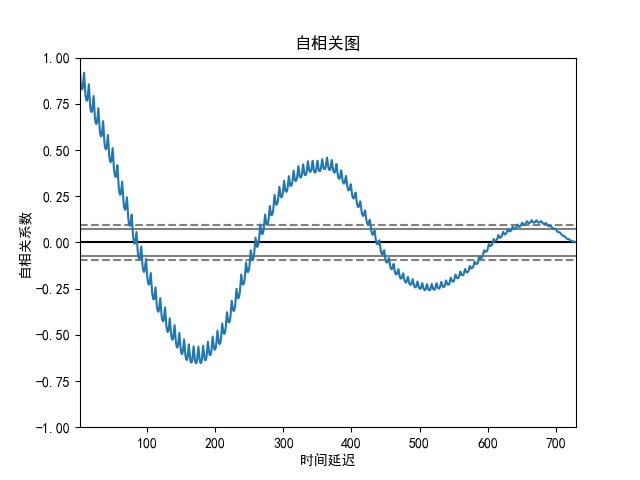
另外,也可以看到 k = 365 k=365 k=365 时,自相关性也比较显著。这意味着,当前数据,与前年数据存在则较大的正相关性。
同理,可以看到 k = 180 k= 180 k=180 时,也即当前的数据,和半年前的数据,存在较大的线性负相关性。
图中,虚线代表,相关性在统计学上不显著。
也即,在计算自相关性的同时,我们也对 x t x_t xt 和 x t − k x_{t-k} xt−k 进行相关性检验,其原假设为: H 0 : ρ ≠ 0 H_0: \\rho \\neq 0 H0:ρ=0,即原假设为 x t x_t xt 和 x t − k x_{t-k} xt−k 存在相关性, ρ \\rho ρ 为 x t x_t xt 和 x t − k x_{t-k} xt−k 的总体 的相关性。
检验统计量:
n
−
2
⋅
r
1
−
ρ
2
∼
t
n
−
2
\\frac{\\sqrt{n-2} \\cdot r} {\\sqrt{1-\\rho^2}} \\sim t_{n-2}
1−ρ2n−2⋅r∼tn−2
r
r
r 为样本
x
t
x_t
xt 和
x
t
−
k
x_{t-k}
xt−k 的相关系数。
取显著水平 α = 0.05 , 0.01 \\alpha=0.05, 0.01 α=0.05,0.01 ,计算出相应的 t n − 2 ( α ) t_{n-2}(\\alpha) tn−2(α),从而得到 r c r i t i c a l r_{critical} rcritical 分别对应虚线和实线。若 r ≤ r c r i t i c a l r\\leq r_{critical} r≤rcritical 则拒绝原假设,即有 95% 或 99% 的把握认为数据不存在相关性。
数据标准化
为了消除数据的量纲不同带来的影响,如温度和负荷都带有不同的量纲,我们需要对数据进行标准化,公式如下:
x
′
=
x
−
x
ˉ
std
(
x
)
x^{\\prime} = \\frac{x-\\bar{x}}{\\text{std}(x)}
x′=std(x)x−xˉ
其中
std
(
x
)
\\text{std}(x)
std(x) 是数据的标准差,其计算公式如下:
std
(
x
)
=
∑
i
=
1
n
(
x
i
−
x
ˉ
)
2
n
−
1
\\text{std}(x) = \\sqrt{\\frac{\\sum_{i=1}^n (x_i-\\bar{x})^2}{n-1}}
std(x)=n−1∑i=1n