《搜索和推荐中的深度匹配》——2.3 搜索中的潜在空间模型

Posted 2021-06-26 卓寿杰_SoulJoy

接下来，我们以潜在空间为基础介绍匹配模型。【1】中找到了搜索中语义匹配的完整介绍。具体来说，我们简要介绍了在潜在空间中执行匹配的代表性搜索方法，包括偏最小二乘（PLS）【2】，潜在空间中的规则化匹配（RMLS）【3】，以及监督语义索引（SSI）【4】【5】。

2.3.1 偏最小二乘

偏最小二乘（PLS）是最初提出的用于统计回归的一种技术【6】。结果表明，PLS可用于学习潜在空间模型进行搜索【7】。

让我们考虑使用方程 (2.4) 中的匹配函数 f (q, d)。我们还假设映射函数定义为 $\phi (q)=L_{q}q$和 ${\phi }^{\prime }(d)=L_{d}d$，其中 q 和 d 是表示查询 q 和文档 d 的特征向量，$L_q$ 和 $L_d$ 是正交矩阵。因此，匹配函数变为

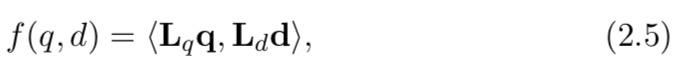
其中 $L_q$ 和 $L_d$ 将被学习。
给定训练数据，$L_q$ 和 $L_d$ 的学习相当于使用约束优化目标函数（基于pointwise loss）：

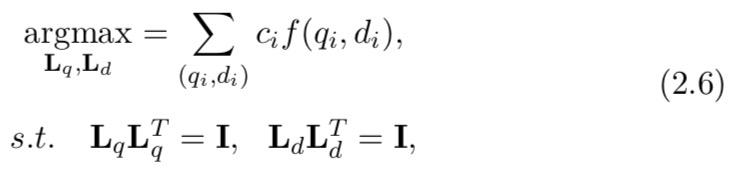
其中 $(q_i,d_i)$ 是一对query和文档，$c_i$ 是这对的点击数，I 是单位矩阵。这是一个非凸优化问题，然而，全局最优是存在的，可以通过使用 SVD（奇异值分解）来实现【7】。

2.3.2 到潜在空间的正则化映射

PLS 假设映射函数是正交矩阵。当训练数据量很大时，学习变得困难，因为它需要解决时间复杂度高的SVD。为了解决这个问题，【8】提出了一种称为潜在空间中的正则化匹配 (RMLS) 的新方法，其中在解决方案稀疏的假设下，PLS 中的正交约束被$l_1$和$l_2$正则化替换。这样就不需要求解SVD，可以高效的进行优化。具体来说，优化问题变成了使用$l_2$和$l_2$约束最小化目标函数（基于逐点损失）的问题：

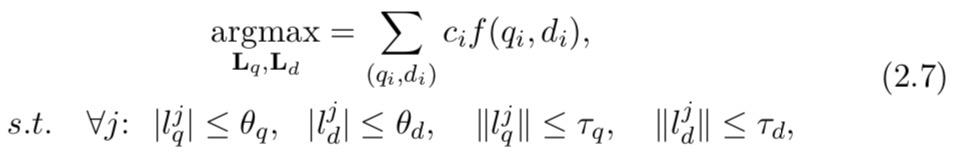
其中 $(q_i,d_i)$ 是一对query和文档，$c_i$ 是这对的点击次数，$L_q$ 和 $L_d$ 是线性映射矩阵，$l_q^j$ 和 $l_d^j$ 是 $L_q$ 和 $L_d$ 的第 j 行向量，${\theta }_q，{\theta }_d、{\tau }_q和{\tau }_d$ 是阈值。$|\cdot |和||\cdot ||$分别表示 l1 和 l2 范数。请注意，正则化是在行向量上定义的，而不是在列向量上定义的。使用 l2 范数是为了避免结果太小。

RMLS中的学习也是一个非凸优化问题。不能保证可以找到全局最优解。解决问题的一种方法是采用替代优化，即先固定$L_q并优化L_d，然后固定L_d并优化L_q$，重复直到收敛。可以很容易地看到，优化可以逐行和逐列地分解和执行矩阵。这意味着 RMLS 中的学习可以轻松并行化和扩展。

方程（2.5）中的匹配函数可以改写为双线性函数:

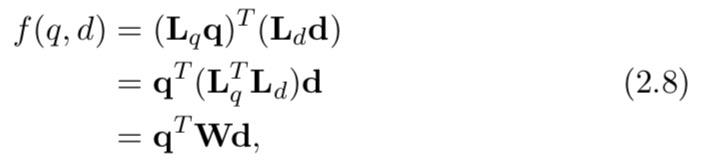
其中 $W=L_q^T{L}_d$。因此，PLS 和 RMLS 都可以看作是一种学习双线性函数的方法，矩阵 W 可以分解为两个低秩矩阵 $L_q和L_d$。

2.3.3 监督语义索引

在 PLS 和 RMLS 中可以做一个特殊的假设；即query空间和文档空间具有相同的维度。例如，当query和文档都表示为词袋时，它们在查询和文档空间中具有相同的维度。结果，方程（2.8）中的 W 变成了一个方阵。 Bai等人提出的监督语义索引（SSI）方法【9】正是做出了这个假设。它进一步将 W 表示为低秩和对角保留矩阵：

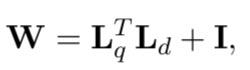
其中 I 表示单位矩阵。因此，匹配函数变为：

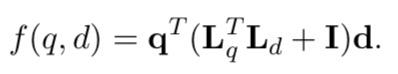
单位矩阵的添加意味着 SSI 在使用低维潜在空间和使用经典向量空间模型 (VSM) 之间进行权衡。 矩阵 W 的对角线对出现在query和文档中的每项给出一个分数。

给定点击数据，首先导出有序的query文档对，表示为$P=(q_1,d_1^{+},d_1^{-}),...,(q_M,d_M^{+},d_M^{-})$ 其中 $d^{+}$排名高于 $d^{-}$，M 是对的数量。学习的目标是选择 $L_q和L_d$，使得$f(q,d^{+})>f(q,d^{-})$对所有对都成立。使用成对损失函数。优化问题变为

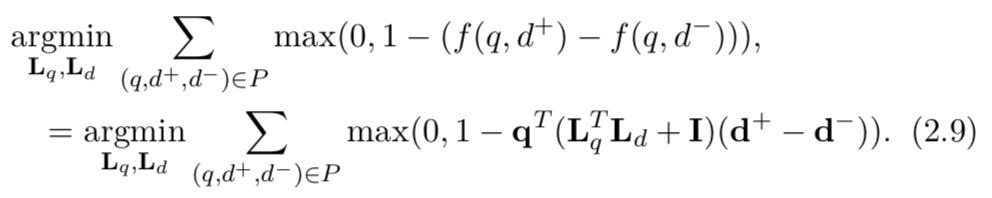
SSI的学习也是一个非凸优化问题，不能保证找到全局最优解。可以以类似于 RMLS 的方式进行优化。

引文

【1】Li，H. and J. Xu (2014). “Semantic matching in search”. Foundations and Trends in Information Retrieval. 7(5): 343–469.
【2】Rosipal, R. and N. Krämer (2006). “Overview and recent advances in partial least squares”. In: Proceedings of the 2005 International
Conference on Subspace, Latent Structure and Feature Selection.
SLSFS’05. Bohinj, Slovenia: Springer-Verlag. 34–51.
【3】Wu, W., Z. Lu, and H. Li (2013b). “Learning bilinear model for matching
queries and documents”. Journal of Machine Learning Research. 14(1): 2519–2548. url: http://dl.acm.org/citation.cfm?id=2567709. 2567742.
【4】Bai, B., J. Weston, D. Grangier, R. Collobert, K. Sadamasa, Y. Qi, O. Chapelle, and K. Weinberger (2009). “Supervised semantic indexing”. In: Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM ’09. Hong Kong, China: ACM. 187– 196.
【5】Bai, B., J. Weston, D. Grangier, R. Collobert, K. Sadamasa, Y. Qi, O. Chapelle, and K. Weinberger (2010). “Learning to rank with
(a lot of) word features”. Information Retrieval. 13(3): 291–314.
【6】Rosipal, R. and N. Krämer (2006). “Overview and recent advances in partial least squares”. In: Proceedings of the 2005 International
Conference on Subspace, Latent Structure and Feature Selection.
SLSFS’05. Bohinj, Slovenia: Springer-Verlag. 34–51.
【7】Wu, W., H. Li, and J. Xu (2013a). “Learning query and document
similarities from click-through bipartite graph with metadata”. In:
Proceedings of the Sixth ACM International Conference on Web
Search and Data Mining. WSDM ’13. Rome, Italy: ACM. 687–696.
【8】Wu, W., Z. Lu, and H. Li (2013b). “Learning bilinear model for matching
queries and documents”. Journal of Machine Learning Research. 14(1): 2519–2548. url: http://dl.acm.org/citation.cfm?id=2567709. 2567742.
【9】Bai, B., J. Weston, D. Grangier, R. Collobert, K. Sadamasa, Y. Qi, O. Chapelle, and K. Weinberger (2009). “Supervised semantic indexing”. In: Proceedings of the 18th ACM Conference on Information and Knowledge Management. CIKM ’09. Hong Kong, China: ACM. 187– 196.