Prim普利姆与Kruskal克鲁斯卡尔算法（Java版）

Posted 2021-06-26 ZSYL

Prim&Kruskal

• Prim算法
• • 基本概念
  • 代码实现
• Kruskal算法
• • 基本概念
  • 代码展示

生活中最小生成树的应用十分广泛.
比如：要连通n个城市需要n－1条边线路，那么怎么样建设才能使工程造价最小呢？
可以把线路的造价看成权值求这几个城市的连通图的最小生成树。
求最小造价的过程也就转化成求最小生成树的过程，则最小生成树表示使其造价最小的生成树。

最小生成树相关概念：

带权图：边赋以权值的图称为网或带权图，带权图的生成树也是带权的，生成树T各边的权值总和称为该树的权。

最小生成树（MST）：权值最小的生成树。

生成树和最小生成树的应用：要连通n个城市需要n－1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。

最小生成树的性质：

MST性质：假设G＝(V,E)是一个连通网，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。

构造网的最小生成树必须解决下面的问题：

（1）每次都选取权值最小的边，但不能构成回路，构成环路的边则舍弃。

（2）遇到权值相等，又均不构成回路的边，随意选择哪一条，均不影响生成树结果。

（3）选取n－1条恰当的边以连通n个顶点。

Prim算法

基本概念

Prim算法基本思想：

假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。
算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

Prim算法的核心:始终保持TE中的边集构成一棵生成树。

其实Prim算法创建最小生成树的主要思路就是从候选节点中选择最小的权值添加到最小生成树中。

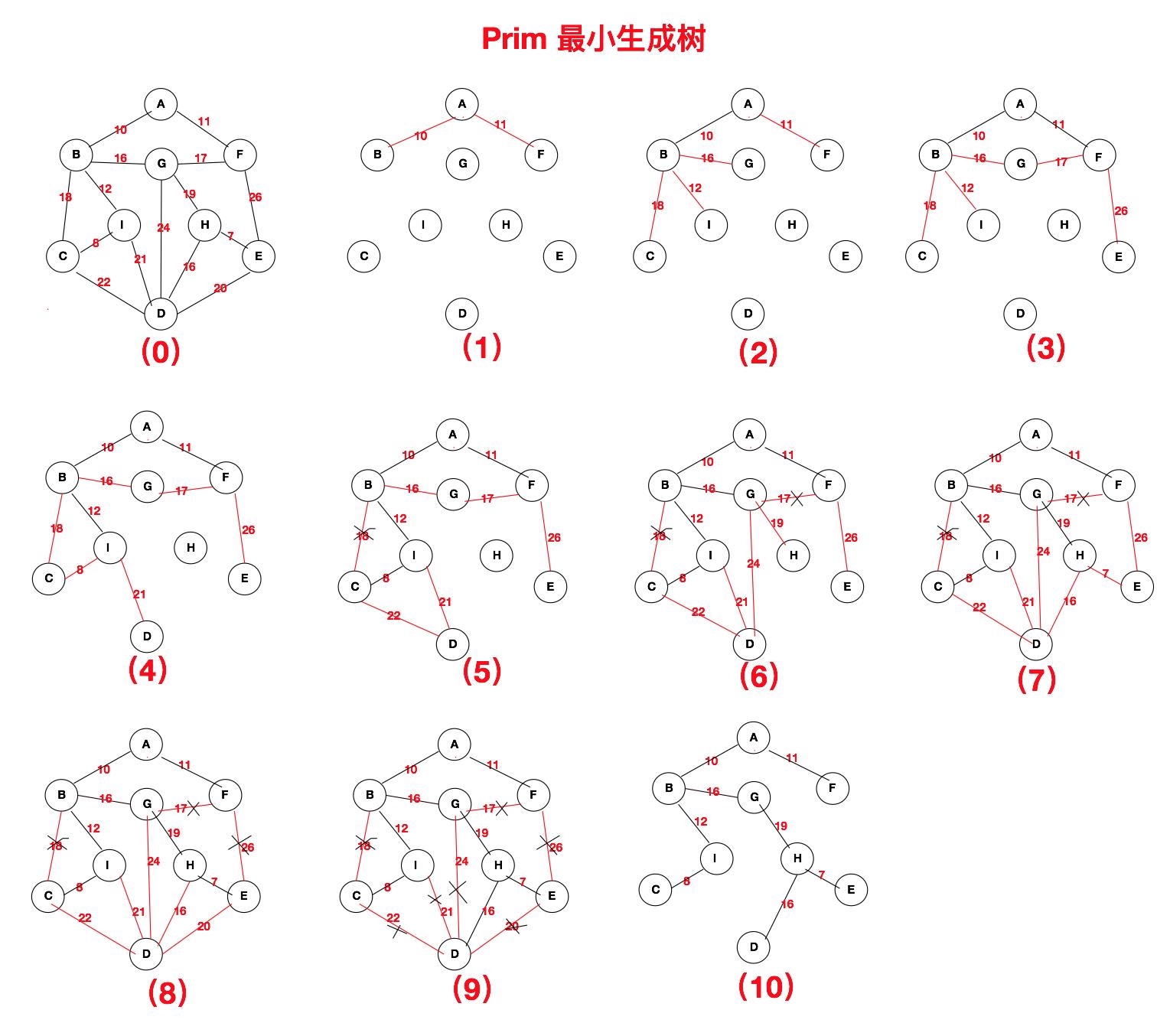
下图是我们之前创建的图使用Prim算法创建最小生成树的完整过程。红色的边就是每一步所对应的候选节点做连的弧，从这些候选的边中选出权值最小的边添加到最小生成树中，我们可以将其视为转正的过程。

一个节点转正后，将其转正节点所连的弧度视为候选弧度，当然这些候选弧度所连的节点必须是最小生成树上以外的点。如果候选弧度所连的点位于最小生成树上，那么将该候选节点抛弃。直到无候选弧度时，最小生成树的创建就完成了。

下图就很好的表述了这个过程，每一步候选节点间的连接使用红色标记，而转正的节点间的弧度使用黑色表示。按照下方这个思路，最终就会生成我们需要的最小生成树。

代码实现

维护一个 tempWeight数组：表示当前权值最小边的尾结点。

package graph;

class MinSpanTree {
   // 邻接矩阵
   int[][] matrix;
   // 表示正无穷， 即没有道路
   int MAX_WEIGHT = Integer.MAX_VALUE;
   // 顶点个数
   int size;
   /**
    *  普里姆算法实现最小生成树：先初始化拿到第一个顶点相关联的权值元素放入数组中，找到其中权值最小的顶点下标，将该下标顶点的权值加入数组中，循环处理
    */
   public void prim() {
       // 存放当前到全部顶点的最小权值的数组，如果已经遍历过的顶点权值为0，无法到达则为正无穷
       int[] tempWeight = new int[size];

       // 当前到下一个最小权值顶点的最小权值
       int minWeight;
       // 当前到下一个最小权值的顶点
       int minId;

       // 权值总和
       int sum = 0;

       // 第一个顶点时，到其他顶点的权值即为邻接矩阵的第一行
       for (int i = 0; i < size; i++) {
           tempWeight[i] = matrix[0][i];
       }

       System.out.println("从v0顶点开始查找");
       for (int i = 1; i < size; i++) {
           // 每次循环找出当前到下一个最小权值的顶点极其最小权值
           minWeight = Integer.MAX_VALUE;
           minId = 0;
           for (int j = 1; j < size; j++) {
               // 权值为0的顶点已经遍历过
               if (tempWeight[j] != 0 && tempWeight[j] < minWeight) {
                   minWeight = tempWeight[j];
                   minId = j;
               }
           }

           // 找到目标顶点minId， 权值minWeight
           System.out.println("找到顶点：v" + minId + "权值为："+ minWeight);
           sum += minWeight;

           // 算法的核心所在： 将目标顶点到各个顶点的权值与当前tempWeight数组中的权值比较，如果前者比后者到某个顶点的权值更小，将前者到这个顶点的权值更新入后者
           tempWeight[minId] = 0;
           for (int j = 1; j < size; j++) {
               if (tempWeight[j] != 0 && matrix[minId][j] < tempWeight[j]) {
                   tempWeight[j] = matrix[minId][j];
               }
           }
       }
       System.out.println("最小权值总和为：" + sum);
   }
}

第二种实现方式：
BF每次从顶点U（已访问的结点）中找权值最小的边。

void prim(int v) {
   // 标记结点：是否访问过
    boolean[] isVisited = new boolean[this.size];
    // 将当前顶点标记已访问
    isVisited[v] = true;

    // 边是顶点个数减一
    for (int i = 1; i < this.size; i++) {
        int h1 = -1;  // 记录已访问的结点
        int h2 = -1;  // 记录未访问的点
        int minWeight = 10000;  // 设置为最大找到小的来替换
        // 从已访问点到未访问点找最短路径
        for (int j = 0; j < this.size; j++) {
            // 如果i点已访问， 找到未访问的点
            if (isVisited[j]) {
                // 遍历其他点，找到未访问的
                for (int k = 0; k < this.size; k++) {
                    // 如果k顶点未被访问， 并且i，j之间距离小于找到的最短距离
                    if (!isVisited[k] && this.matrix[j][k] < minWeight) {
                        minWeight = this.matrix[j][k];
                        h1 = j;
                        h2 = k;
                    }
                }
            }
        }
        System.out.println(h1+"--"+h2+minWeight);
        isVisited[h2] = true;
    }
}

Kruskal算法

基本概念

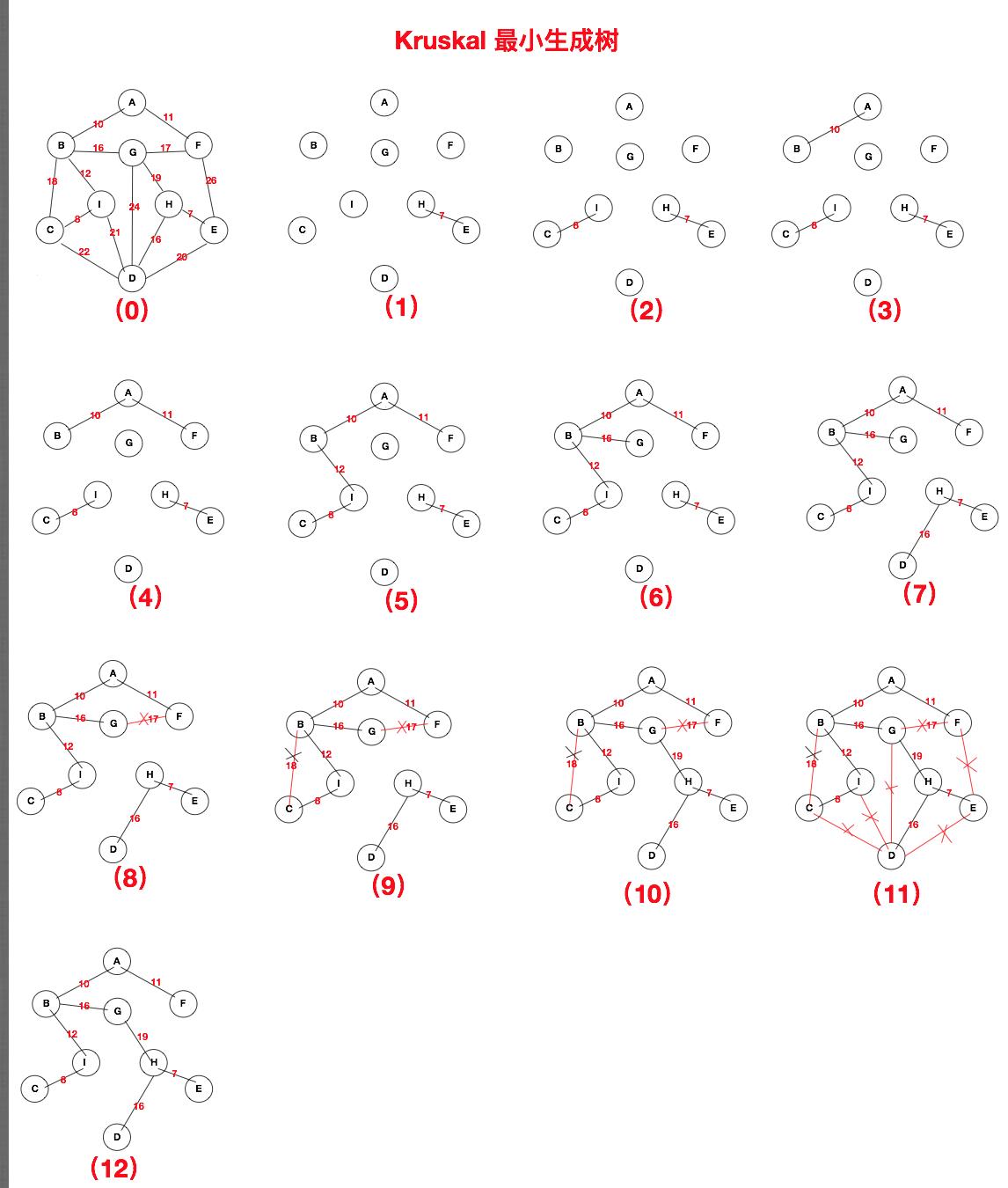
克鲁斯卡尔（Kruskal） 算法从另一途径求网的最小生成树。其基本思想是：假设连通网G=（V，E），令最小生成树的初始状态为只有n个顶点而无边的非连通图T=（V，{}），图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止。

克鲁斯卡尔算法的基本思想是以边为主导地位，始终选择当前可用的最小边权的边。

每次选择边权最小的边链接两个端点是kruskal的规则，并实时判断两个点之间有没有间接联通（回路）。

过程如下：

代码展示

import java.util.HashSet;
import java.util.Set;

/**
 * 克鲁斯卡尔算法：最小生成树的构建过程
 */
public class KruskalAlgorithm {
    int verxs;
    int[][] weight;
    int[] data;

    public void kruskal(){
        int edgeNum=0;  //边的数量
        Set<Integer> verxset=new HashSet<>();  // 点的集合
        // 最小生成树边的个数是(顶点个数-1)，以此作为循环条件
        while(edgeNum != this.verxs-1){
            int min=Integer.MAX_VALUE;
            // 找到图中最小的边
            int v1=-1;
            int v2=-1;
            for(int i=0;i<this.verxs;i++){
                for(int j=0;j<this.verxs;j++){
                    if(this.weight[i][j]<min){
                        min=this.weight[i][j];
                        v1=i;
                        v2=j;
                    }
                }
            }
            // 假定该边符合条件，将顶点加入集合，边数+1
            verxset.add(v1);
            verxset.add(v2);
            edgeNum++;

            // 如果边的个数大于等于点的个数，存在环（充分不必要条件，如果每个点都有边将其连接，则逆命题也成立
            if(verxset.size() <= edgeNum){
                // 该边不符合条件，边数-1
                edgeNum--;
            } else {  // 该边符合条件，输出
                System.out.println(data[v1]+"-"+data[v2]+",权值为"+this.weight[v1][v2]);
            }

            //排除该边（这会影响原图，如果不想影响原图，需要将weiht复制一份）
            this.weight[v1][v2]=Integer.MAX_VALUE;
            this.weight[v2][v1]=Integer.MAX_VALUE;
        }
    }
}

第二种方式：

运用贪心思想，将边按照权值升序排序，每次选择权值最小的边，并判断是否构成回路。

public void kruskal() {
   Scanner sc = new Scanner(System.in);
   // lambda表达式重写排序算法，按照权值升序
   PriorityQueue<Edge> queue = new PriorityQueue<>((o1, o2)-> o1.weight-o2.weight);
   Set<Integer> verxset=new HashSet<>();  // 点的集合
   int edgeNum=0;  //边的数量

   // 获取边信息
   for (int i = 0; i < 10; i++) {
       queue.add(new Edge(sc.nextInt(), sc.nextInt(), sc.nextInt()));
   }

   // 最小生成树边的个数是(顶点个数-1)，以此作为循环条件
   while(edgeNum != this.verxs-1){
       // 获取当前最短边
       Edge curedge = queue.poll();
       // 假定该边符合条件，将顶点加入集合，边数+1
       verxset.add(curedge.x);
       verxset.add(curedge.y);
       edgeNum++;

       // 如果边的个数大于等于点的个数，存在环（充分不必要条件，如果每个点都有边将其连接，则逆命题也成立
       if(verxset.size() <= edgeNum){
           // 该边不符合条件，边数-1
           edgeNum--;
       } else {  // 该边符合条件，输出
           System.out.println(curedge.x+"-"+ curedge.y+",权值为"+ curedge.weight);
       }
   }
}
class Edge {
    int x;  // 起点
    int y;  // 终点
    int weight;  // 权值
    public Edge(int x, int y, int w) {
        this.x = x;
        this.y = y;
        this.weight = w;
    }
}

参考内容：

百度百科
Link

站在巨人肩膀上前进

感谢!