实验五 基于MATLAB的模拟滤波器设计
Posted 毛_三月
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了实验五 基于MATLAB的模拟滤波器设计相关的知识,希望对你有一定的参考价值。
目录
一、实验目的:
1.加深对模拟滤波器常用指标的理解;
2.学会模拟滤波器中的频率变换;
3.根据指标要求设计模拟滤波器,并进行信号的处理。
二、实验原理:
模拟滤波器的设计是其它滤波器设计的基础,其设计原理见课本。利用MATLAB设计模拟滤波器的调用函数见课本。常用的函数格式如下:
1.巴特沃斯模拟滤波器
[N,wc]=buttord(wp,ws,Ap,As,’s’)
[b,a]=butter(N,wc,’ftype’,’s’)
函数buttord的输入参数wp和ws(rad/s)分别表示滤波器的通带和阻带截频,Ap和As(dB)表示滤波器的通带和阻带衰减。‘s’表示所设计的是模拟滤波器。函数buttord返回的参数N是滤波器的阶数,wc为BW型滤波器3dB的截频。
利用函数butter获得BW型滤波器的分子多项式系数(b)和分母多项式系数(a)。
‘ftype’表示要设计滤波器的型号,当设计的为低通或带通滤波器是这个参数可以缺省。当ftype=high时,函数butter获得BW型高通滤波器的分子多项式系数(b)和分母多项式系数(a);当当ftype=stop时,函数butter获得BW型带阻滤波器的分子多项式系数(b)和分母多项式系数(a);
或者:
N=buttord(wp,ws,Ap,As,’s’); wc=wp/(10^(0.1*Ap)-1)^(1/2/N); [b,a]=butter(N,wc, ’ftype’,’s’);
或者:
N=buttord(wp,ws,Ap,As,’s’); wc=ws/(10^(0.1*As)-1)^(1/2/N); [b,a]=butter(N,wc, ’ftype’,’s’);
2.切比雪夫Ⅰ型滤波器
[N,wc]=cheb1ord(wp,ws,Ap,As,’s’);
[b,a]=cheby1(N,Ap,wc, ’ftype’,’s’);
或者,
N=cheb1ord(wp,ws,Ap,As,’s’);wc=wp; [b,a]=cheby1(N,Ap,wc, ’ftype’,’s’)
或者
N=cheb1ord(wp,ws,Ap,As,’s’); [b,a]=cheby1(N,Ap,wp, ’ftype’,’s’);
3. 切比雪夫Ⅱ型滤波器
[N,wc]=cheb2ord(wp,ws,Ap,As,’s’)
[b,a]=cheby2(N,As,wc, ’ftype’,’s’)
或者
N=cheb2ord(wp,ws,Ap,As,’s’);wc=ws; [b,a]=cheby2(N,As,wc, ’ftype’,’s’)
或者
N=cheb2ord(wp,ws,Ap,As,’s’); [b,a]=cheby2(N,As,ws, ’ftype’,’s’)
4.椭圆滤波器
[N,wc]=ellipord(wp,ws,Ap,As,’s’);
[b,a]=ellip(N,Ap,As,wc, ’ftype’,’s’);
或者
N= ellipord (wp,ws,Ap,As,’s’);wc=wp; [b,a]=ellip(N,Ap,As,wc, ’ftype’,’s’);
或者
N= ellipord (wp,ws,Ap,As,’s’); [b,a]=ellip(N,Ap,As,wp, ’ftype’,’s’);
5.模拟域频率变换
MATLAB提供了实现模拟域频率变换的函数,他们分别是:
(1)模拟低通到高通变换
[numt,dent] = lp2hp(num,den,W0)
高通中,一般W0=1。
(2)模拟低通到带通变换
[numt,dent] = lp2bp(num,den,W0,B)
(3)模拟低通到带阻变换
[numt,dent] = lp2bs(num,den,W0,B)
其中,num,den分别表示变换前模拟低通滤波器系统函数的分子多项式系数和分母多项式系数,W0和B为变换中的参数。numt,dent分别表示变换后模拟滤波器系统函数的分子多项式系数和分母多项式系数,
6.补充函数
(1)buttap函数用来返回设计的BW滤波器的零点、极点和增益。函数调用格式为:
[z,p,k]=buttap(N);
其中,z,p,k分别为滤波器系统函数H(S)的零点、极点和增益,N为滤波器的阶数。
(2)cheb1ap函数用来返回设计的CB Ⅰ型滤波器的零点、极点和增益,cheb2ap函数用来返回设计的CB Ⅱ滤波器的零点、极点和增益。其调用格式为:
[z,p,k]= cheb1ap (N,Rp);
[z,p,k]= cheb2ap (N,Rs);
其中,z,p,k分别为滤波器系统函数H(S)的零点、极点和增益,N为滤波器的阶数,Rp为滤波器在通带内的最大衰减值,Rs为滤波器在阻带内的最小衰减值。
(3)zp2tf函数,函数调用格式为:
[b,a]=zp2tf (z,p,k);
其中,z,p,k分别为滤波器系统函数H(S)的零点、极点和增益,b、a分别为滤波器系统函数H(s)的分子和分母多项式的系数,
(4)freqs函数用来求解模拟滤波器的频率响应。其函数调用格式为:
h=freqs(b,a,w);
[h,w]=freqs(b,a,n);
其中,b,a分别为滤波器系统函数H(s)的分子和分母多项式的系数,w表示频率点,n表示进行复频率响应的点数,其默认值为512。如果没有输出参数而直接调用freqs(b,a,w函数时,将直接画出复频率响应的幅频响应和相频响应。
freqs函数用来求解模拟滤波器的频率响应。
三、例题:
1.BW模拟低通滤波器的幅频特性曲线
程序如下:
clear all
for i=1:4
switch i
case 1
N=2;
case 2
N=5;
case 3
N=10;
case 4
N=20;
end
[z,p,k]=buttap(N);
[b,a]=zp2tf(z,p,k);
[H,w]=freqs(b,a);
magH2=(abs(H)).^2;
hold on
plot(w,magH2);
axis([0 2 0 1.1]);
end
xlabel('w/wc'); ylabel('/H(jw)/^2')
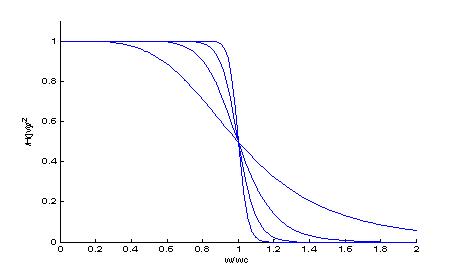
2、(1)设计一个巴特沃斯模拟低通滤波器,技术指标为:通带截频1000Hz,阻带截频1500Hz,通带波纹1dB,阻带衰减50dB。
(2)假设一个信号x(t)=sin(2pif1t)+sin(2pif2t)+sin(2pif3*t),其中f1=100Hz,f2=2000Hz,f3=2900Hz,信号的采样频率为10000Hz。将原信号与通过该滤波器的模拟信号进行比较。
clear all
wp=1000 *2*pi;
ws=1500*2*pi;
Ap=1;
As=50;
[N,wc]=buttord(wp,ws,Ap,As,'s'); %求的滤波器的最小阶数和截止频率
[b,a]=butter(N,wc,'s'); %设计模拟巴特沃斯滤波器
w=linspace(0,4000,1000)*2*pi; %设置绘制频率响应的频率点
H=freqs(b,a,w); % 计算给定频率点的复数频率响应
figure(1)
plot(w/2/pi, 20*log10(abs(H)));
xlabel('频率/Hz');ylabel('振幅/dB');
grid on;
% 计算Ap,As
w1=[wp ws];
h=freqs(b,a,w1);
fprintf('Ap=%.4f\\n',-20*log10(abs(h(1))));
fprintf('As=%.4f\\n',-20*log10(abs(h(2))));
fs=10000;
dt=1/fs; %模拟信号采样间隔
f1=100;f2=2000;f3=2900;
t=0:dt:0.1;
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t);
H=[tf(b,a)]; %滤波器在MATLAB中的表示
y=lsim(H,x,t); % 模拟输出
figure(2)
subplot(2,1,1)
plot(t,x);
xlabel ('(a)输入信号');
subplot(2,1,2)
plot(t,y);
xlabel('(b)输出信号');
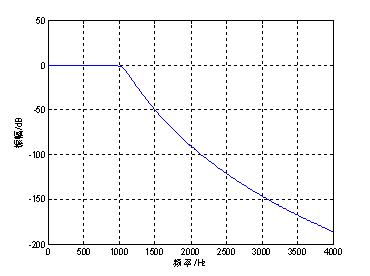
图1 模拟低通滤波器的幅度响应函数
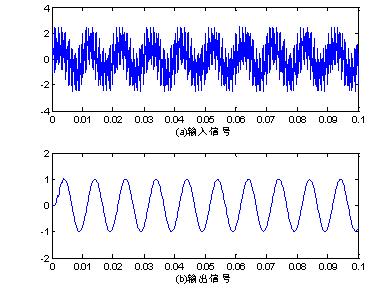
图2 滤波器的输入输出函数
Ap=0.9053; As=50.0000
2.设计一个巴特沃斯模拟带通滤波器,技术指标为:通带频率:1000-2000Hz,两侧过渡带宽500Hz,通带波纹1dB,阻带衰减100dB。
方法一:
clear all
wp1=1000*2*pi;
wp2=2000*2*pi;
ws1=500*2*pi;
ws2=2500*2*pi;
B=wp2-wp1;
W0=sqrt(wp1*wp2);
Ap=1;
As=100;
ws11=(ws1^2-W0^2)/(B*ws1); %带通到低通的频率变换
ws22=(ws2^2-W0^2)/(B*ws2);
wp=1;
ws=min(abs(ws11),abs(ws22)); %低通滤波器的阻带截频
[N,wc]=buttord(wp,ws,Ap,As,'s'); %求的滤波器的最小阶数和截止频率
[b,a]=butter(N,wc,'s'); %设计模拟巴特沃斯滤波器
[c,d]=lp2bp(b,a,W0,B); %将低通变换为带通
w=linspace(1,3000,1000)*2*pi; %设置绘制频率响应的频率点
H=freqs(c,d,w); % 计算给定频率点的复数频率响应
plot(w/2/pi,abs(H));
xlabel('频率/Hz');ylabel('振幅/dB');
grid on;
% 计算Ap,As
w1=[wp1 wp2 ws1 ws2];
h=freqs(c,d,w1);
fprintf('Ap1=%.4f\\n',-20*log10(abs(h(1))));
fprintf('Ap2=%.4f\\n',-20*log10(abs(h(2))));
fprintf('As1=%.4f\\n',-20*log10(abs(h(3))));
fprintf('As1=%.4f\\n',-20*log10(abs(h(4))));
运行结果:
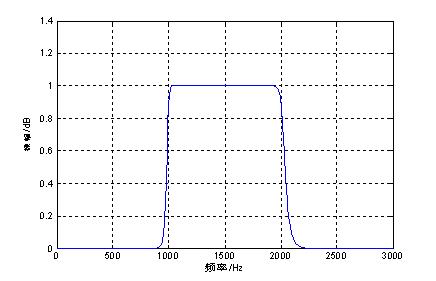
图3 带通滤波器的幅度响应函数
Ap1=0.9713;Ap2=0.9716;As1=244.2668;As1=100.0000
方法二:
程序如下:
clear all
wp=[1000 2000]*2*pi;
ws=[500 2500]*2*pi;
Ap=1;
As=100;
[N,wc]=buttord(wp,ws,Ap,As,'s'); %求的滤波器的最小阶数和截止频率
[b,a]=butter(N,wc,'s'); %设计模拟巴特沃斯滤波器
w=linspace(1,3000,1000)*2*pi; %设置绘制频率响应的频率点
H=freqs(b,a,w); % 计算给定频率点的复数频率响应
plot(w/2/pi,abs(H));
xlabel('频率/Hz');ylabel('振幅/dB');
grid on;
% 计算Ap,As
w1=[wp ws];
h=freqs(b,a,w1);
fprintf('Ap1=%.4f\\n',-20*log10(abs(h(1))));
fprintf('Ap2=%.4f\\n',-20*log10(abs(h(2))));
fprintf('As1=%.4f\\n',-20*log10(abs(h(3))));
fprintf('As1=%.4f\\n',-20*log10(abs(h(4))));
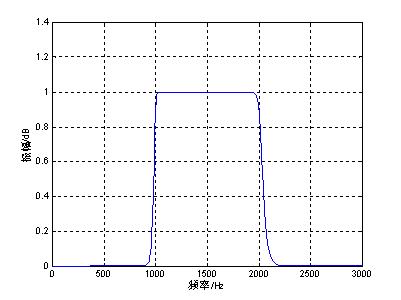
图3 带通滤波器的幅度响应函数
Ap1=0.9724;Ap2=0.9721;As1=244.2646;As1=99.9998
四、作业:
1.假设一个信号x(t)= sin(2pif1t)+0.5cos(2pif2t),其中f1=20Hz,f2=100Hz。
(1)请设计一个模拟滤波器能把f2滤除掉,请写出程序,并画出原信号与原信号通过滤波器的输出信号的图形。
clear all
wp=52*2*pi;
ws=80*2*pi;
Ap=1;
As=50;
[N,wc]=buttord(wp,ws,Ap,As,'s'); %求的滤波器的最小阶数和截止频率
[b,a]=butter(N,wc,'s'); %设计模拟巴特沃斯滤波器
w=linspace(0,500,1000)*2*pi; %设置绘制频率响应的频率点
H=freqs(b,a,w); % 计算给定频率点的复数频率响应
figure(1)
plot(w/2/pi, 20*log10(abs(H)));
xlabel('频率/Hz');ylabel('振幅/dB');
grid on;
% 计算Ap,As
w1=[wp ws];
h=freqs(b,a,w1);
fprintf('Ap=%.4f\\n',-20*log10(abs(h(1))));
fprintf('As=%.4f\\n',-20*log10(abs(h(2))));
fs=10000;
dt=1/fs; %模拟信号采样间隔
f1=20;f2=100;
t=0:dt:0.1;
x=sin(2*pi*f1*t)+0.5*cos(2*pi*f2*t);
H=[tf(b,a)]; %滤波器在MATLAB中的表示
y=lsim(H,x,t); % 模拟输出
figure(2)
subplot(2,1,1)
plot(t,x);
xlabel ('(a)输入信号');
subplot(2,1,2)
plot(t,y);
xlabel('(b)输出信号');
(2)请设计一个模拟滤波器能把f1滤除掉,请写出程序,并画出原信号与原信号通过滤波器的输出信号的图形。
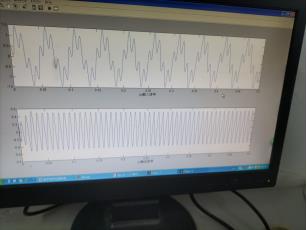
2.假设一个信号x(t)=sin(2pif1t)+sin(2pif2t)+sin(2pif3*t),其中f1=200Hz,f2=1500Hz,f3=2900Hz,信号的采样频率为10000Hz。
(1)请设计一个模拟滤波器将f2保留,f1和f3滤除。
cle以上是关于实验五 基于MATLAB的模拟滤波器设计的主要内容,如果未能解决你的问题,请参考以下文章