PCA与梯度上升法
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了PCA与梯度上升法相关的知识,希望对你有一定的参考价值。
PCA
PCA:主成分分析算法,具体记录在:《特征值分解实验:人脸识别与PageRank网页排序》,本质就是矩阵的特征值分解。
PCA 是一个非监督学习的算法,主要用于数据降维,方便人类理解、可视化、去噪。
举个例子,二维平面的降维:

那怎么把二维降到一维呢?选一个特征即可,另一个特征扔调。
- 降到特征1:所有点都在X轴上,二维平面变成一条横线。

- 降到特征2:所有点都在Y轴上,二维平面变成一条竖线。

对比以上俩者,发现降维到X轴,是更好的保持了原来样本之间的距离,那我们应该选降维到特征1(X轴)。
但是,这么简单粗暴的降维,丢失的信息就太多了(特征2整个维度的信息都没有了),请问还有木有更好的方案呢?
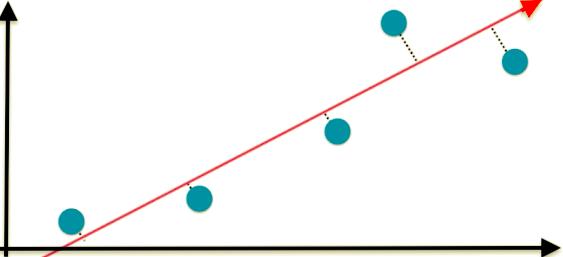
有的,综合特征1、特征2,取一条斜线,所有的点更加趋紧原来点分布的情况。
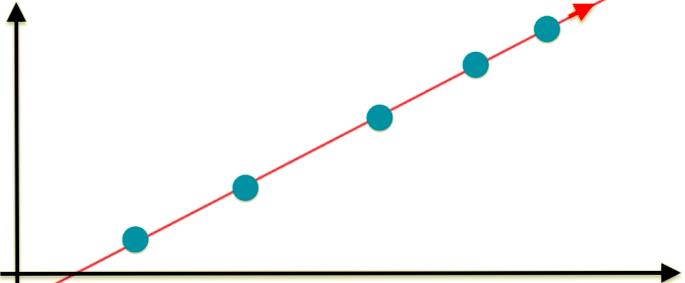
是的,理论上这个斜轴才是最接近原样本距离分布的,同时问题变成了,咱们如何找到这个轴(让样本间的间距最大的轴)呢?
为了找到这个轴,需要知道样本间的间距,那我们用什么来定义/表达样本间的间距呢?
在统计学中,方差可以用于表达样本间的间距。
-
方差:描述样本整体分布的疏密的指标
-
V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 Var(x)=\\frac{1}{m}\\sum\\limits_{i=1}^m(x^{i}-\\overline{x})^{2} Var(x)=m1i=1∑m(xi−x)2
现在问题换成方差的方式表达:找到一个轴,使得样本空间的所有点映射到轴上后,方差最大。
第一步(demean):将样例的均值归零。
所有的样本都减去这批样本整体的均值,这样做的作用是什么?如下图所示:
demean 前:
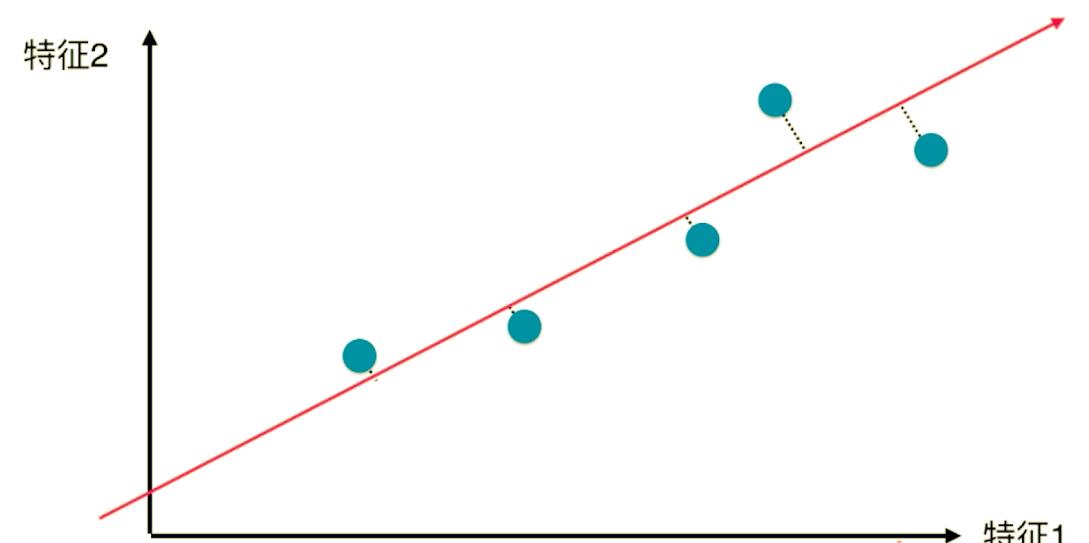
demean 后:
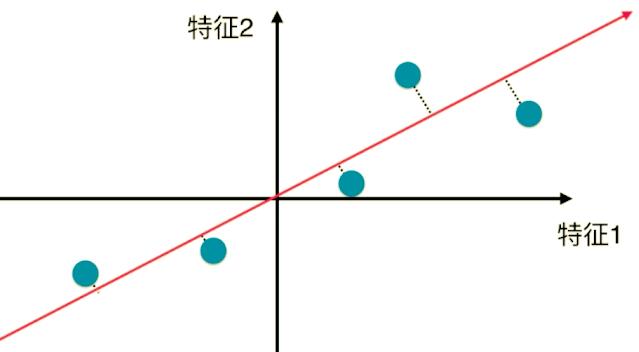
样本的分布没有改变,同时坐标轴移动了 — 使得样本在每一个维度的均值都为零(
x
‾
=
0
\\overline{x}=0
x=0)。
-
方差公式: V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 Var(x)=\\frac{1}{m}\\sum\\limits_{i=1}^m(x^{i}-\\overline{x})^{2} Var(x)=m1i=1∑m(xi−x)2
-
demean后: V a r ( x ) = 1 m ∑ i = 1 m ( x i ) 2 Var(x)=\\frac{1}{m}\\sum\\limits_{i=1}^m(x^{i})^{2} Var(x)=m1i=1∑m(xi)2
这就是demean的作用(归零),式子化简了,计算更方便。
【拓展】为什么经过均值归零后,这个红色的轴就变到过坐标原点了?证明如下。
首先,所有的点均值归零以后,意味着所有的点在这条直线上的投影的均值也为 0。
下面是以数据点在二维平面上为例,进行的证明。(数据点是n为同理)
整体证明思路是,假设有一组样本数据X,已经经过了demean,即各个分量的平均值为0,假设存在一个坐标轴w(w只表示坐标轴的方向,为一个单位向量),则这组样本数据映射到w后,其各个分量的平均值依然为0。
如果投影到一条直线上以后,各个维度的均值都为 0,则这条直线一定过原点。
简单证明如下。以二维空间为例:假设这条直线的方程是 x 2 = k ∗ x 1 + b x_{2} = k * x_{1} + b x2=k∗x1+b。
因为我们现在已知所有点在所有维度的均值都为 0,即
- s u m ( x 1 ) m = 0 \\frac{sum(x1)}{m} = 0 msum(x1)=0
- s u m ( x 2 ) m = 0 \\frac{sum(x2)}{m} = 0 msum(x2)=0
也就是 s u m ( x 1 ) = 0 、 s u m ( x 2 ) = 0 sum(x1) = 0、sum(x2)= 0 sum(x1)=0、sum(x2)=0。
我们将所有的 x 1 ( i ) x1(i) x1(i) 和 x 2 ( i ) x2(i) x2(i) 带入直线方程,就有了 m 个 x 2 ( i ) = k ∗ x 1 ( i ) + b x2(i) = k * x1(i) + b x2(i)=k∗x1(i)+b。
将这 m 个式子加起来,就是 s u m ( x 2 ) = k ∗ s u m ( x 1 ) + m ∗ b sum(x2) = k * sum(x1) + m * b sum(x2)=k∗sum(x1)+m∗b。
因为知道了 s u m ( x 1 ) = 0 、 s u m ( x 2 ) = 0 sum(x1) = 0、sum(x2) = 0 sum(x1)=0、sum(x2)=0。
所以, m ∗ b = 0 m * b = 0 m∗b=0,得到 b = 0 b = 0 b=0。
证毕。
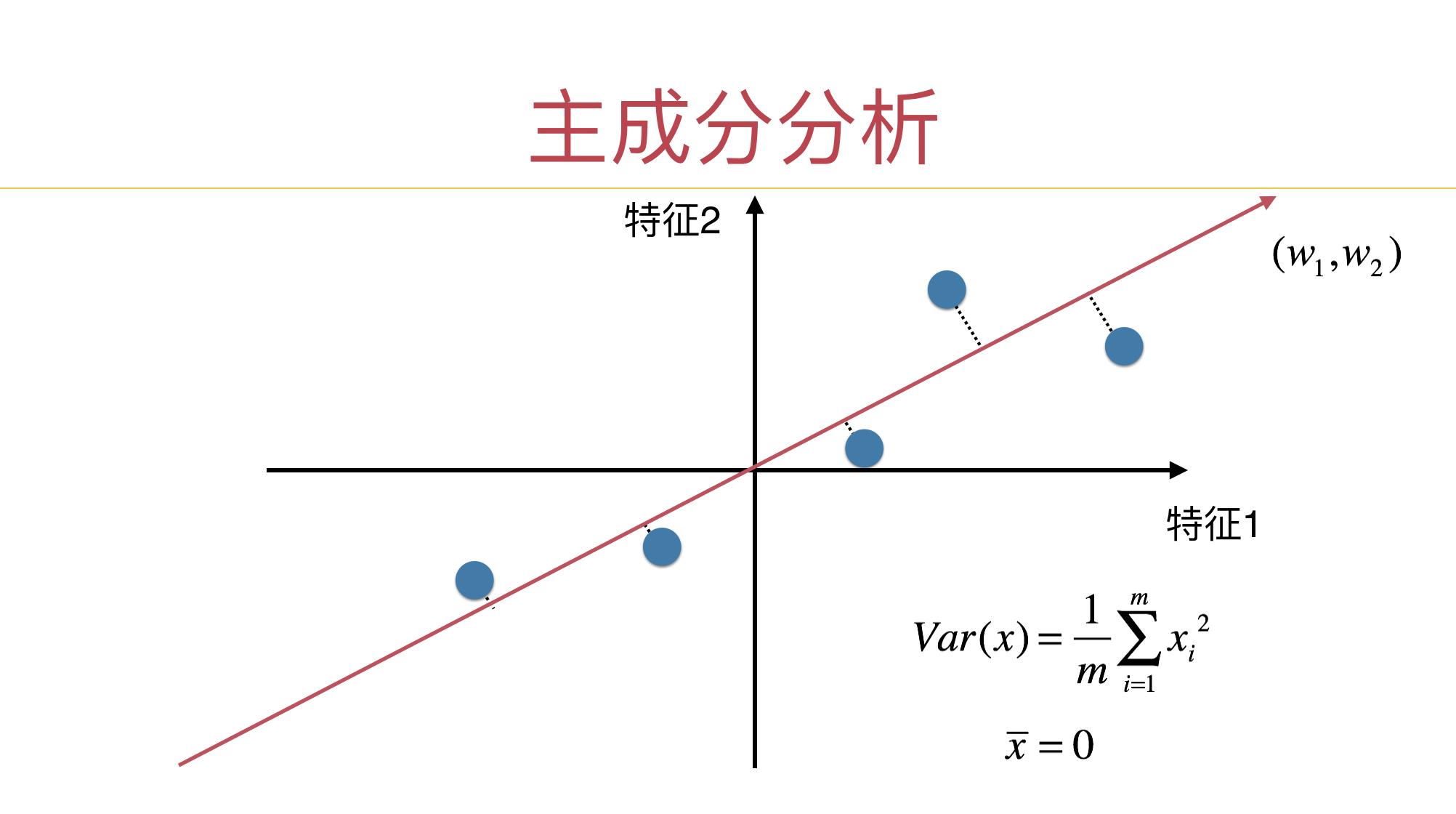
我们求图中的红轴,就是 求出w 的方向。
因为 w 代表一个坐标轴,对于2维数据,我们要求的第一主成分,就是上图中的红色向量方向。对于坐标轴,我们知道方向就好了。
【拓展】已知直线,如何求方向向量?
- 在直线上任取两点,用一点坐标减去另外一点坐标就是直线的方向向量。如直线y=3x
- 取点(0,0)、(1,3)
- 用(1,3)减去(0,0)得方向向量(1,3)
已知 x ‾ = 0 \\overline{x}=0 x=0,
- demean前的方差公式: V a r ( x ) = 1 m ∑ i = 1 m ∣ ∣ x i ∣ ∣ 2 Var(x)=\\frac{1}{m}\\sum\\limits_{i=1}^m||x^{i}||^{2} Var(x)=m1i=1∑m∣∣xi∣∣2
- demean后的方差公式: V a r ( x p r o j e c t ) = 1 m ∑ i = 1 m ∣ ∣ x p r o j e c t i ∣ ∣ 2 Var(x_{project})=\\frac{1}{m}\\sum\\limits_{i=1}^m||x_{project}^{i}||^2 Var(xproject)=m1i=1∑m∣∣xprojecti∣∣2
其中, x x x 变成了 x p r o j e c t x_{project} xproject ,这个怎么解释呢?
- x x x:原样本
- x p r o j e c t x_{project} xproject:映射到 w 轴上的样本
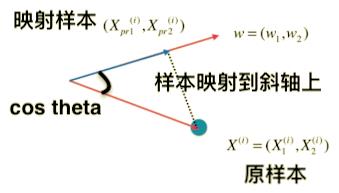
X
i
X_{i}
Xi 映射到
w
w
w轴 上,就是向 w 轴作一个垂直的直线,交点的位置就是
x
p
r
o
j
e
c
t
i
x_{project}^{i}
xprojecti。
使得 V a r ( x p r o j e c t ) = 1 m ∑ i = 1 m ∣ ∣ x p r o j e c t i ∣ ∣ 2 Var(x_{project})=\\frac{1}{m}\\sum\\limits_{i=1}^m||x_{project}^{i}||^2 Va以上是关于PCA与梯度上升法的主要内容,如果未能解决你的问题,请参考以下文章
