MATLABFOA优化算法整定PID控制器参数—— 一阶带时延的被控对象

Posted 2021-06-26 昔时扬尘处

【MATLAB】FOA优化算法整定PID控制器参数（五）—— 一阶带时延的被控对象

目录

• 【MATLAB】FOA优化算法整定PID控制器参数（五）—— 一阶带时延的被控对象
• • 1研究背景
  • 2果蝇优化算法的简单介绍
  • • 2.1FOA算法的简单介绍
    • 2.2FOA算法的案例实现
  • 3被控对象与适应度函数的设计
  • • 3.1被控对象的传递函数
    • 3.2适应度函数的设计
    • 3.3FOA算法的PID参数整定实现
  • 4算法结果

1研究背景

写在前面：
 1.本代码基于MATLAB2019a版本，低版本或者不同版本可能会报错，mdl文件或slx文件打开可能会失败；
 2.如果运行时间过长，请观察迭代次数是否有变化。
 3.本博客附上算法运行图并详细介绍，如果转载请注明出处；
 4.如果本博客恰巧与您的研究有所关联，欢迎您的咨询qq1366196286；

---

---

  参考前面的几篇博客

【Simulink】PSO优化算法整定PID控制器参数（一）

【Simulink】PSO算法优化Simulink模型的参数在线整定（二）

【MATLAB】GA优化算法整定PID控制器参数（三）—— 一阶带时延的被控对象

【MATLAB】NSGA-2优化算法整定PID控制器参数（四）—— 一阶带时延的被控对象

2果蝇优化算法的简单介绍

  基础的概念请参考文献：
  [1] 张继荣,张天.基于改进粒子群算法的PID控制参数优化[J].计算机工程与设计,2020,41(04):1035-1040.
  [2] 张娟. 基于果蝇算法优化PID参数的永磁同步电机控制系统研究[D].湖南科技大学,2017.
  [3] 赵晓军,刘成忠,胡小兵.基于果蝇优化算法的PID控制器设计与应用[J].中南大学学报(自然科学版),2016,47(11):3729-3734.
  [4] 龚育林.基于模糊PID自适应整定参数的反应釜温度控制系统[J].东莞理工学院学报,2021,28(01):102-106.
  [5] 李明辉,曹泽,王玉洁.基于自适应果蝇优化算法的PID参数优化[J].机床与液压,2018,46(20):144-147.

2.1FOA算法的简单介绍

  2011年台湾亚东技术学院的潘文超受果蝇觅食行为的启发，提出了一种的全局优化算法—果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）。

  该算法的优点在于计算过程简单、易于编码实现和易于理解等。果蝇优化算法（FOA）和蚁群算法（Ant Colony Optimization, ACO）、粒子群算法（Particle Swarm Optimization,PSO）类似，属于群体智能，或者说是群智能算法的范畴，它们都必须通过迭代搜索才能找到最优解。

  FOA的基本概述如下：果蝇优化算法是一种基于果蝇觅食行为推演出寻求全局优化的新方法。果蝇本身在感官知觉上优于其他物种，尤其在嗅觉与视觉上，果蝇嗅觉器官能很好地搜集漂浮于空气中的各种气味，甚至能嗅到40公里以外的食物源，然后，飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且向该方向飞去。果蝇优化算法（FOA）通过模拟果蝇利用敏锐的嗅觉和视觉进行捕食的过程，FOA实现对解空间的群体迭代搜索。果蝇优化算法依据果蝇优越的嗅觉和敏锐的视觉特性，对其寻食过程进行仿真模拟，进而获得一种全局优化进化的新方法。果蝇的嗅觉器官能够对空气中飘浮的各种气味，产生超强的感知能力和搜索能力，而且在食物周围可以通过敏锐的视觉察觉食物和同伴，从而能够顺利地飞向目标。

  因此，FOA算法的基本思想是：根据果蝇优越的嗅觉器官对食物进行搜索，而果蝇和食物之间的距离与食物的味道浓度相关，即距离越近，其味道浓度越大。果蝇搜索食物的实质过程就是其渐渐地从味道浓度淡的位置飞向味道更浓的位置的过程。依据果蝇优化算法(FOA)搜索食物的生理特性，图1中将其概况为以下几个步骤。

---

1. Step 1 初始化，设定群体规模Sizepop 和最大迭代次数Maxgen，以及随机产生果蝇群体的初始坐标位置Xaxis 和Yaxis 。

$$\{\begin{array}{l}\text{ int }{X}_{-}\text{axis }\\ \text{ int }{Y}_{-}\text{axis }\end{array}$$

2. Step 2 给出果蝇运用嗅觉器官寻找食物的随机方向与距离。

$$\{\begin{array}{l}{X}_{\mathrm{i}}=X_{\text{axis }}+V_{\text{Value }}{\ast }_{\text{rand }}()\\ Y_{\mathrm{i}}=Y_{\text{axis }}+V_{\text{Value }}\ast r_{\text{rand }}()\end{array}$$

3. Step 3 因为没有办法获知食物的位置，所以先计算果蝇个体与原点之间的距离计算味道浓度判定值Si。

$$\begin{array}{rl}{D}_{{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}}_{\mathrm{i}}}& =\sqrt{X_{\mathrm{i}}^2+Y_{\mathrm{i}}^2}\\ S_i& =1/D_{{\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}}_{\mathrm{i}}}\end{array}$$

4. Step 4 将味道浓度判定值Si代入味道浓度判定函数(或称作适应度函数)中，从而得到果蝇个体的味道浓度。

$$S_{{\text{smell }}_{\mathrm{i}}}=F_{\text{Function }}\left(S_{\mathrm{i}}\right)$$

5. Step 5 从该果蝇群体中找到味道浓度最优的果蝇个体。

$$\left[b_{\text{bestsmell }}{b}_{\text{bestindes }}\right]=\min \left(S_{\text{Smell }}\right)$$

6. Step 6 记录并保留下最优味道浓度bbestSmell与其X、Y的坐标，这时候果蝇群体利用视觉向该位置飞去。

$$\{\begin{array}{l}{S}_{\text{Smellbest }}=b_{\text{bestSmell }}\\ X_{\text{axis }}=X\left(b_{\text{bestIndex }}\right)\\ Y_{\text{axis }}=Y\left(b_{\text{bestIndex }}\right)\end{array}$$

7. Step 7 进入迭代寻优，将步骤（2）~（5）循环进行，判断当前最佳味道浓度是否优于前一迭代最佳味道浓度，并且当前迭代次数是否小于最大迭代数MMaxgen；若是则执行步骤（6）。

---

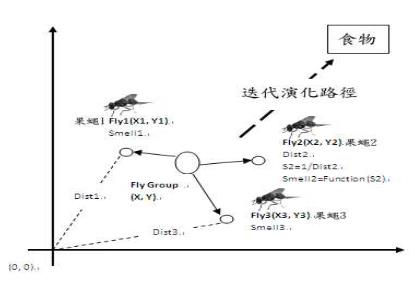
图1 果蝇优化算法迭代示意图

  与其他群智能优化算法相比较，果蝇优化算法不但具有算法简单、程序代码容易实现、更快地收敛于最优解 的优点，而且比其他的群智能算法调整的参数少 。由于难以将参数间的复杂关系研究清楚，若选取不适的参数，会直接涉及到算法的优化性能，并且会加深算法复杂度分析的难度，因此采用果蝇优化算法设计的PID控制器，能够在参数的选取上减少一些困扰。而且果蝇优化算法的运行时间较少，可以减少计算复杂度 。

%*** 清空运行环境
clc;
clear all; %#ok<CLALL>
tic;

%*** 设置参数
maxgen = 200; %迭代次数
sizepop = 50; %种群规模
% [ yy, Xbest, Ybest  ] = FOA( maxgen, sizepop );

%% /******算法运行*******/
%maxgen为迭代次数，sizepop为种群规模
    %*** 随机初始果蝇群里位置
    X_axis = 10 * rand();
    Y_axis = 10 * rand();

    %*** 果蝇寻优开始，利用嗅觉寻找食物
    for i=1 : sizepop

        %*** 赋予果蝇个体利用嗅觉搜寻食物之随机方向与距离
        X(i) = X_axis + 2 * rand() - 1;
        Y(i) = Y_axis + 2 * rand() - 1;

        %*** 由于无法得知食物位置，因此先估计与原点的距离（Dist），再计算味道浓度判定值（S），此值为距离的倒数
        D(i) = (X(i)^2 + Y(i)^2)^0.5;
        S(i) = 1 / D(i);

        %*** 味道浓度判定值（S）代入味道浓度判定函数（或称为Fitness function），以求出该果蝇个体位置的味道浓度（Smell(i))
        Smell(i) = Fitness(S(i));

    end

    %*** 找出此果蝇群里中味道浓度最低的果蝇（求极小值）
    [bestSmell bestindex] = min(Smell);

    %*** 保留最佳味道浓度值与x，y的坐标，此时果蝇群里利用视觉往该位置飞去
    X_axis = X(bestindex);
    Y_axis = Y(bestindex);
    Smellbest = bestSmell;

    %*** 果蝇迭代寻优开始
    for g=1 : maxgen

        %*** 赋予果蝇个体利用嗅觉搜寻食物的随机方向和距离
        for i=1 : sizepop
            X(i) = X_axis + 2 * rand() - 1;
            Y(i) = Y_axis + 2 * rand() - 1;

            %*** 由于无法得知食物位置，因此先估计与原点的距离（Dist），再计算味道浓度判定值（S），此值为距离的倒数
            D(i) = (X(i)^2 + Y(i)^2)^0.5;
            S(i) = 1 / D(i);

            %*** 味道浓度判定值（S）代入味道浓度判定函数，以求出该果蝇个体位置的味道浓度（Smell(i))
            Smell(i) = Fitness(S(i));

        end

        %*** 找出此果蝇群里中味道浓度最低的果蝇（求极小值）
        [bestSmell bestindex] = min(Smell);

        %*** 判断味道浓度是否优于前一次迭代味道浓度，若是则保留最佳味道浓度值与x，y的坐标，此时果蝇群体利用视觉往该位置飞去
        if bestSmell < Smellbest
            X_axis = X(bestindex);
            Y_axis = Y(bestindex);
            Smellbest = bestSmell;
        end

        %*** 每次最优Semll值记录到yy数组中，并记录最优迭代坐标
        yy(g) = Smellbest;
        Xbest(g) = X_axis;
        Ybest(g) = Y_axis;
    end
toc;
%*** 绘制迭代味道浓度与果蝇飞行路径趋势图
figure(1);
plot(yy);
title('Optimization process', 'fontsize', 12);
xlabel('Iteration Number', 'fontsize', 12);
ylabel('Smell', 'fontsize', 12);
figure(2);
plot(Xbest, Ybest, 'b.');
title('Fruit fly flying route', 'fontsize', 14);
xlabel('X-axis', 'fontsize', 12);
ylabel('Y-axis', 'fontsize', 12);

%% 适应度评价函数
function [ y ] = Fitness( x )
    %味道浓度判定函数
    y = x^2 - 5;
end

---

2.2FOA算法的案例实现

  以下表为测试函数，函数形式、搜索区间和函数最优值，如下表所示。

  以Rastrigin为测试函数

$$\mathrm{Ras}(\mathrm{x})=20+x_1^2+x_2^2-10\left(\cos 2\pi x_1+\cos 2\pi x_2\right)$$

function [ y ] = Fitness(x1,x2)
    %味道浓度判定函数
    y=20+x1.^2+x2.^2-10*(cos(2*pi*x1)+cos(2*pi*x2));
end

求解极小值函数曲线如下

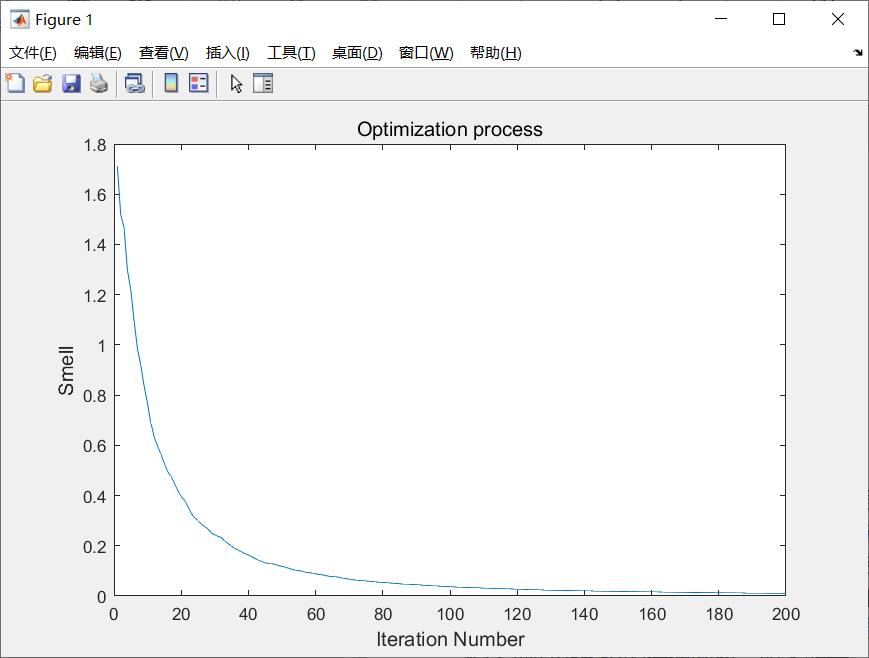
图2 求解极小值函数曲线图

果蝇搜寻轨迹如下

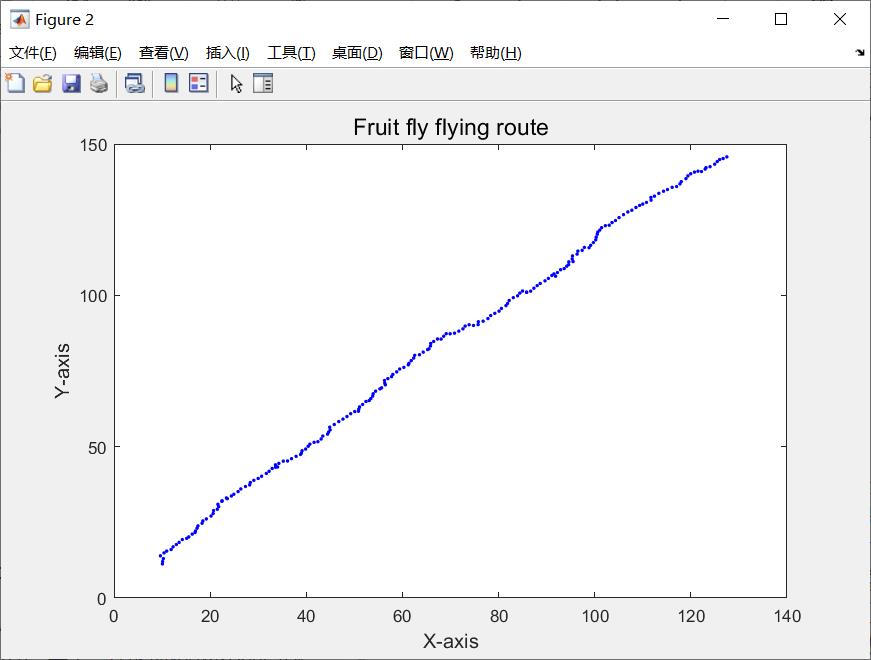
图3 果蝇搜寻轨迹

3被控对象与适应度函数的设计

3.1被控对象的传递函数

  以下式二阶Ⅰ型时延系统的传递函数为例，运用NSGA-2算法进行PID参数优化，其中系统设置为采样时间1 ms，指令为单位阶跃信号，仿真运行时间为1.0 s。其中，性能优化函数Best_J采取时间与误差绝对值乘积的积分方程（Integral of Time Multiplied by the Absolute Value of Error，ITAE），同时为避免控制量过大而产生超调，在性能优化函数Best_J中添加PID控制器输入量的平方项。这仅仅是其中某个目标的适应度函数，此外还需设计另外目标的适应度函数，如2.2适应度函数的设计。
  二阶Ⅰ型时延系统的传递函数，如下所示。可按照自己的实际系统进行设计，既可以.m文件进行编写

3.2适应度函数的设计

  为获取较为满意的过渡过程，采用误差绝对值时间积分性能指标作为适应度评价函数Best_J。同时为防止控制输入过大，在Best_J加入控制输入的评分项，如式（1-2）所示。

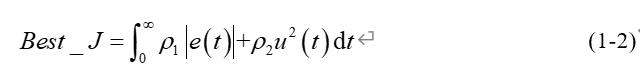
式（1-2）中e(t)为系统输出误差，u(t)为PID控制器输入量，ρ1，ρ2为权重值。
  为避免超调，采用罚函数对超调量进行优先处理，则如式（1-3）所示。

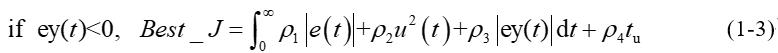
式（1-3）中ρ3>>max(ρ1，ρ2和ρ4)，且y(t)为被控对象输出，ey(t)=y(t)-y(t-1)。
  以此作为目标适应度函数的设计。

3.3FOA算法的PID参数整定实现

  本文算法采用实数编码，对于PID参数寻优中的果蝇个体编码为Kp，Ki和Kd。果蝇优化算法（FOA）整定PID控制器参数具体过程如下。
  Step1：初始化，包括群体规模、最大迭代次数和随机产生果蝇群体位置Xaxis和Yaxis。
  Step2：给定果蝇个体的随机方向、距离。
  Step3：计算果蝇个体与原点之间的距离DDisti，并计算味道浓度判定值Si。
  Step4：将果蝇个体解码为PID控制器参数Kp，Ki和Kd，运行控制系统的Simulink模型，得到该组参数对应的性能指标。
  Step5：将上一步计算得到的性能指标作为果蝇个体的适应值，并判断该适应值是否满足算法停止条件，若满足，结束优化过程，进而得到最佳的PID参数；否则，转到Step6。
  Step6：从果蝇群体中寻找出最优味道浓度的果蝇个体，并记录下最优味道浓度bbestsmell与其X和Y坐标，而后果蝇群体飞向该坐标位置。最终产生新的果蝇群体，转到步骤Step2。

  果蝇优化算法整定PID控制器参数的流程，如图4所示。

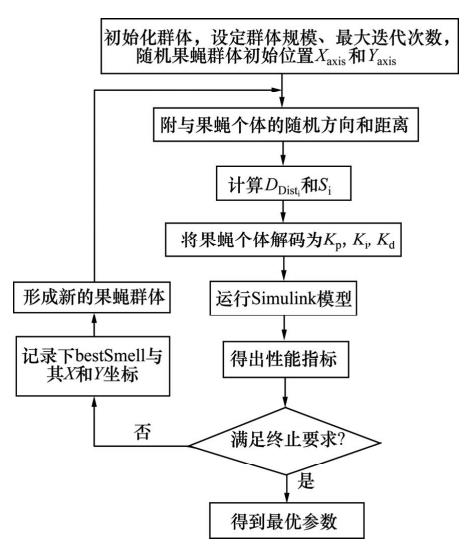
图4 果蝇优化算法整定PID控制器参数的流程图

4算法结果

最佳指标适应度值如下

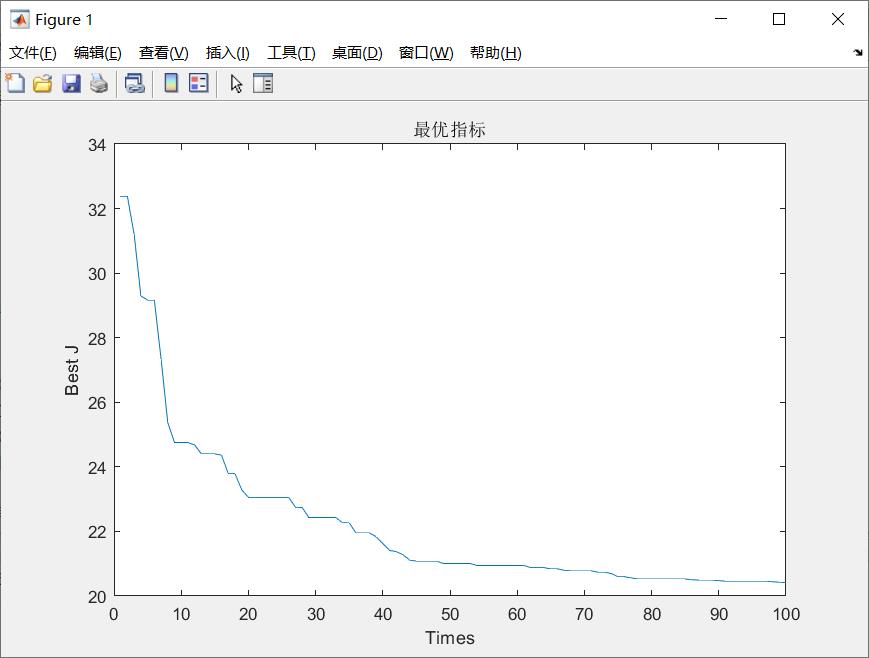
图5 FOA算法的最佳指标适应度函数图

阶跃响应输出如下

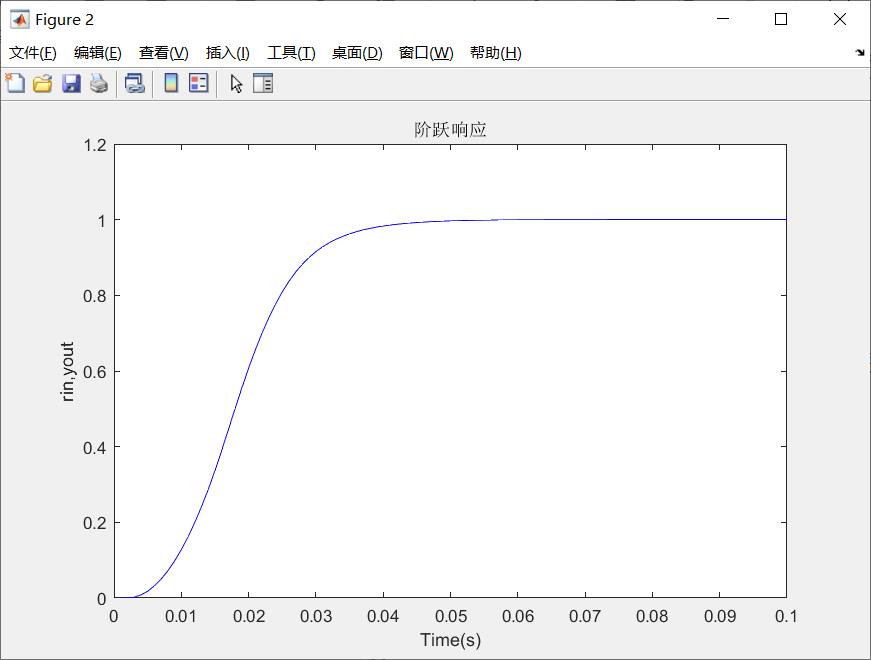
图6 果蝇优化算法整定PID控制器的响应输出

果蝇搜寻轨迹如下

图7 果蝇优化算法Kp的搜寻轨迹

MATLAB不同优化算法整定PID控制器参数—— 一阶带时延的被控对象

MATLAB自适应果蝇优化算法整定PID控制器参数—— 一阶带时延的被控对象

精品课设不同优化算法整定PID控制参数

模糊PID控温算法的具体实现：参数自整定模糊PID算法概念

第三天：SLAM智能小车DIY乐趣-小车控制PID参数整定

模糊控制——模糊自适应整定PID控制