文献阅读16期：Deep Learning on Graphs: A Survey - 5

Posted 2021-06-26 RaZLeon

[ 文献阅读·综述 ] Deep Learning on Graphs: A Survey [1]

推荐理由：图神经网络的survey paper，在很多的领域展现出了独特的作用力，分别通过GRAPH RNN（图循环网络）、GCN（图卷积）、GRAPH AUTOENCODERS（图自编码器）、GRAPH REINFORCEMENT LEARNING（图强化学习模型）、GRAPH ADVERSARIAL METHODS（图对抗模型）等五个类型的模型进行阐述，可以让大家对图神经网络有一个整体的认识。

5.图自动编码器

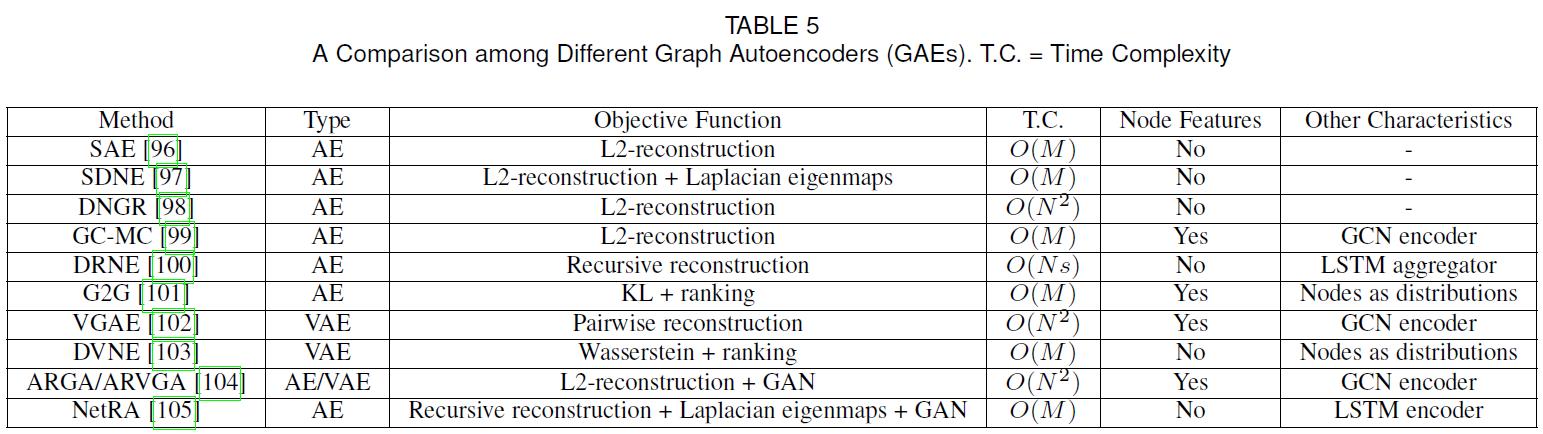
自动编码器（AE）及其变体广泛应用于无监督学习任务中，适合于学习图的节点表示。隐含的假设是，图有一个内在的，潜在的非线性低秩结构。在这一节中，本文首先阐述了图自动编码器，然后介绍了图变分自动编码器和其他改进。下表总结了GAE的主要特征：

5.1.自动编码器

• 图的自动编码器的使用起源于稀疏自动编码器（SAE）。其基本思想是，通过将邻接矩阵或其变化作为节点的原始特征，AEs可以作为一种降维技术来学习低维节点表示。具体而言，SAE采用了以下L2-reconstruction loss：
  $$\begin{array}{c}\underset{\mathbf{\Theta }}{\min }{\mathcal{L}}_2=\sum _{i=1}^N\Vert \mathbf{P}(i,:)-\hat{\mathbf{P}}(i,:){\Vert }_2\\ \hat{\mathbf{P}}(i,:)=\mathcal{G}\left({\mathbf{h}}_i\right),{\mathbf{h}}_i=\mathcal{F}(\mathbf{P}(i,:))\end{array}\text{\hspace{1em}(43)}$$
• 然而，SAE是建立在错误的理论分析基础上的，其有效性的机制尚不清楚。
• Structure deep network embedding（SDNE）填补了这一难题，它表明等式（43）中的L2重建损失实际上对应于节点之间的二阶接近度，即如果两个节点具有相似的邻域，则它们共享相似的latten表示，这是网络科学中一个被广泛研究的概念，被称为协同过滤或三角闭包。由于网络嵌入方法表明一阶邻近性也很重要，SDNE通过添加另一个拉普拉斯特征映射项修改了目标函数：
• $$\underset{\mathbf{\Theta }}{\min }{\mathcal{L}}_2+\alpha \sum _{i,j=1}^N\mathbf{A}(i,j){\Vert {\mathbf{h}}_i-{\mathbf{h}}_j\Vert }_2\text{\hspace{1em}(44)}$$
• 例如，如果两个节点直接相连，它们也共享相似的潜在表示。作者还通过使用邻接矩阵并为零和非零元素分配不同的权重来修改L2重建损失：
• $${\mathcal{L}}_2=\sum _{i=1}^N{\Vert \left(\mathbf{A}(i,:)-\mathcal{G}\left({\mathbf{h}}_i\right)\right)\odot {\mathbf{b}}_i\Vert }_2\text{\hspace{1em}(45)}$$
• GC-MC采用了不同的方法，使用Kipf和Welling提出的GCN作为编码器：
  $$\mathbf{H}=GCN\left({\mathbf{F}}^V,\mathbf{A}\right)\text{\hspace{1em}(46)}$$
  其使用简单的双线性函数作为解码器：
  $$\hat{\mathbf{A}}(i,j)=\mathbf{H}(i,:){\Theta }_{de}\mathbf{H}(j,:{)}^T\text{\hspace{1em}(47)}$$
• DRNE没有重建邻接矩阵或其变体，而是提出了另一种改进方法，通过使用LSTM聚集邻域信息来直接重建低维节点向量。具体而言，DRNE采用了以下目标函数：
  L = ∑ i = 1 N ∥ h i − LSTM ⁡ ( { h j ∣ j ∈ N ( i ) } ) ∥ (48) \\mathcal{L}=\\sum_{i=1}^{N}\\left\\|\\mathbf{h}_{i}-\\operatorname{LSTM}\\left(\\left\\{\\mathbf{h}_{j} \\mid j \\in \\mathcal{N}(i)\\right\\}\\right)\\right\\|\\tag{48} L=i=1∑N​∥hi​−LSTM({hj​∣j∈N(i)})∥(48)
• Graph2Gauss (G2G)将每个节点编码为高斯分布${\mathbf{h}}_i=\mathcal{N}(\mathbf{M}(i,:),\mathrm{diag}(\Sigma (i,:)))$来获得节点的不确定性。具体而言，作者使用从节点属性到高斯分布均值和方差的深度映射作为编码器：
  $$\mathbf{M}(i,:)={\mathcal{F}}_{\mathbf{M}}\left({\mathbf{F}}^V(i,:)\right),\mathbf{\Sigma }(i,:)={\mathcal{F}}_{\mathbf{\Sigma }}\left({\mathbf{F}}^V(i,:)\right)\text{\hspace{1em}(49)}$$
• 他们不使用显式解码器函数，而是使用成对约束来学习模型：
• $$\begin{array}{r}\mathrm{K}\mathrm{L}\left({\mathbf{h}}_j\Vert {\mathbf{h}}_i\right)<\mathrm{K}\mathrm{L}\left({\mathbf{h}}_{j^{\prime }}\Vert {\mathbf{h}}_i\right)\\ \forall i,\forall j,\forall j^{}\end{array}$$