文献阅读15期：Deep Learning on Graphs: A Survey - 4
Posted RaZLeon
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了文献阅读15期：Deep Learning on Graphs: A Survey - 4相关的知识，希望对你有一定的参考价值。
[ 文献阅读·综述 ] Deep Learning on Graphs: A Survey [1]
推荐理由：图神经网络的survey paper，在很多的领域展现出了独特的作用力，分别通过GRAPH RNN（图循环网络）、GCN（图卷积）、GRAPH AUTOENCODERS（图自编码器）、GRAPH REINFORCEMENT LEARNING（图强化学习模型）、GRAPH ADVERSARIAL METHODS（图对抗模型）等五个类型的模型进行阐述，可以让大家对图神经网络有一个整体的认识。
4.3 提高与探讨
- 这节主要讨论其他的一些可以被应用到图深度学习上的方法。
4.3.1.注意力机制
- 在之前的方法中，大部分图图计算过程中，近邻节点的影响非常大，但这些节点影响的方式是实现制定好的，并非训练得来的。Graph attention network (GAT)引入了一种调整卷及操作的机制：
h i l + 1 = ρ ( ∑ j ∈ N ^ ( i ) α i j l h j l Θ l ) (32) \\mathbf{h}_{i}^{l+1}=\\rho\\left(\\sum_{j \\in \\hat{\\mathcal{N}}(i)} \\alpha_{i j}^{l} \\mathbf{h}_{j}^{l} \\Theta^{l}\\right)\\tag{32} hil+1=ρ⎝⎛j∈N^(i)∑αijlhjlΘl⎠⎞(32)
其中， α i j l \\alpha_{i j}^{l} αijl便是 l t h l^{t h} lth层中指节点 v i v_{i} vi对节点 v j v_{j} vj的注意程度：
α i j l = exp ( LeakyReLU ( F ( h i l Θ l , h j l Θ l ) ) ) ∑ k ∈ N ^ ( i ) exp ( LeakyReLU ( F ( h i l Θ l , h k l Θ l ) ) ) (33) \\alpha_{i j}^{l}=\\frac{\\exp \\left(\\text { LeakyReLU }\\left(\\mathcal{F}\\left(\\mathbf{h}_{i}^{l} \\Theta^{l}, \\mathbf{h}_{j}^{l} \\Theta^{l}\\right)\\right)\\right)}{\\sum_{k \\in \\hat{\\mathcal{N}}(i)} \\exp \\left(\\text { LeakyReLU }\\left(\\mathcal{F}\\left(\\mathbf{h}_{i}^{l} \\Theta^{l}, \\mathbf{h}_{k}^{l} \\Theta^{l}\\right)\\right)\\right)}\\tag{33} αijl=∑k∈N^(i)exp( LeakyReLU (F(hilΘl,hklΘl)))exp( LeakyReLU (F(hilΘl,hjlΘl)))(33) - 下图展示了一种多头注意力机制：
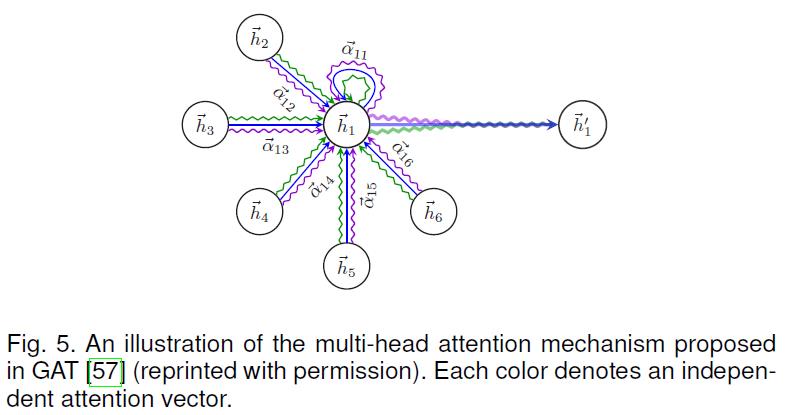
- 至于其他的注意力机制还有两级注意机制，这种机制兼顾了节点级别和语义级别的注意。
4.3.2.残差和跳连
- 一般来说GCN的层数不宜过多，一般2-3层为佳。这个问题可能是由于训练深度GCN的实际困难或过度平滑问题造成的。比如所有深层的节点都是同样的表达。
- 为了解决这一问题，残差连接被引入GCN：
H l + 1 = ρ ( D ~ − 1 2 A ~ D ~ − 1 2 H l Θ l ) + H l (34) \\mathbf{H}^{l+1}=\\rho\\left(\\tilde{\\mathbf{D}}^{-\\frac{1}{2}} \\tilde{\\mathbf{A}} \\tilde{\\mathbf{D}}^{-\\frac{1}{2}} \\mathbf{H}^{l} \\Theta^{l}\\right)+\\mathbf{H}^{l}\\tag{34} Hl+1=ρ(D~−21A~D~−21HlΘl)+Hl(34) - Column network (CLN)采用了一种近似的残差连接，但包含有可训练权重：
h i l + 1 = α i l ⊙ h ~ i l + 1 + ( 1 − α i l ) ⊙ h i l (35) \\mathbf{h}_{i}^{l+1}=\\boldsymbol{\\alpha}_{i}^{l} \\odot \\widetilde{\\mathbf{h}}_{i}^{l+1}+\\left(1-\\boldsymbol{\\alpha}_{i}^{l}\\right) \\odot \\mathbf{h}_{i}^{l}\\tag{35} hil+1=αil⊙h il+1+(1−αil)⊙hil(35)
其中，权重的计算方式为：
α i l = ρ ( b α l + Θ α l h i l + Θ α ′ l ∑ j ∈ N ( i ) h j l ) (36) \\boldsymbol{\\alpha}_{i}^{l}=\\rho\\left(\\mathbf{b}_{\\alpha}^{l}+\\mathbf{\\Theta}_{\\alpha}^{l} \\mathbf{h}_{i}^{l}+\\mathbf{\\Theta}_{\\alpha}^{\\prime l} \\sum_{j \\in \\mathcal{N}(i)} \\mathbf{h}_{j}^{l}\\right)\\tag{36} αil=ρ⎝⎛bαl+Θαlhil+Θα′lj∈N(i)∑hjl⎠⎞(36) - 受个性化PageRank的影响，PPNP定义了一种含有传送信息至初始层的图卷积：
H l + 1 = ( 1 − α ) D ~ − 1 2 A ~ D ~ − 1 2 H l + α H 0 (37) \\mathbf{H}^{l+以上是关于文献阅读15期：Deep Learning on Graphs: A Survey - 4的主要内容，如果未能解决你的问题，请参考以下文章
文献阅读15期：Deep Learning on Graphs: A Survey - 4
文献阅读17期：Deep Learning on Graphs: A Survey - 6
文献阅读16期：Deep Learning on Graphs: A Survey - 5
文献阅读12期：Deep Learning on Graphs: A Survey - 1