0x00 基本算法

Posted 2021-06-26 幽殇默

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了0x00 基本算法相关的知识，希望对你有一定的参考价值。

位运算

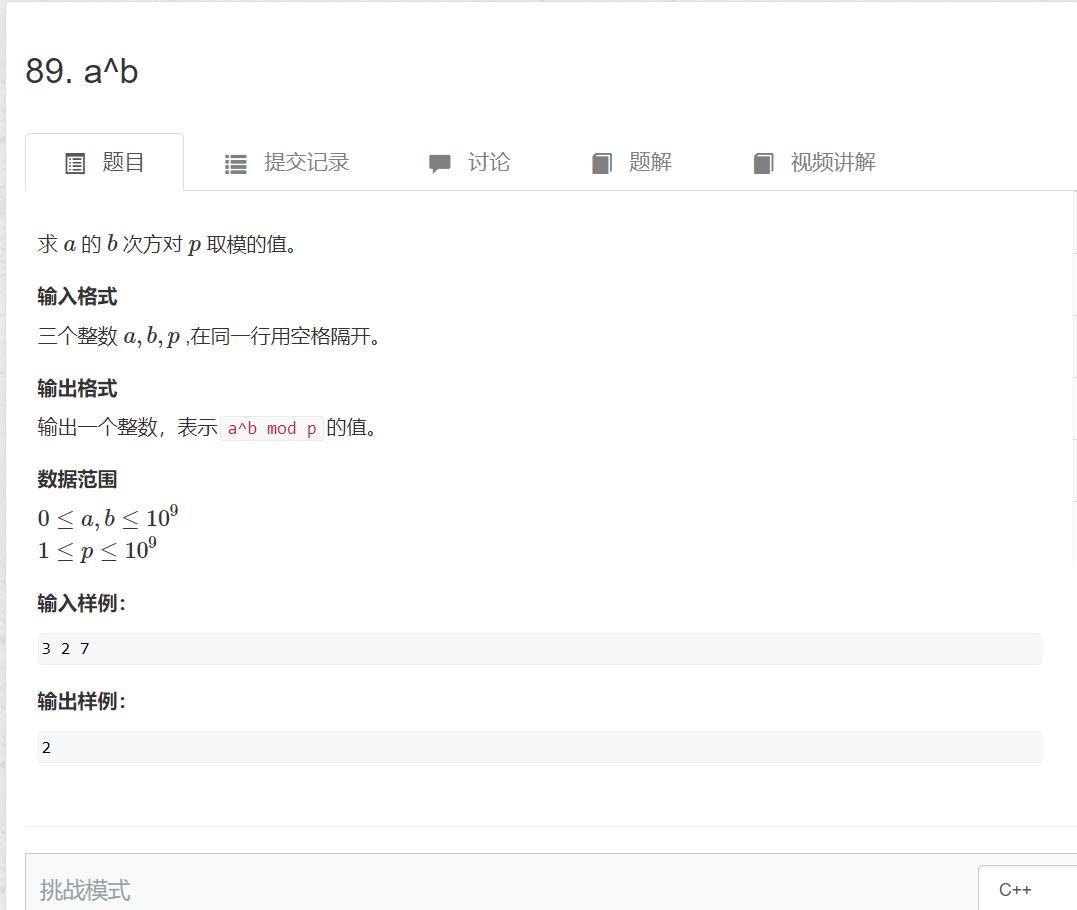
89. a^b

考察的知识点：二进制快速幂

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long LL;
LL a,b,p;
LL quick_mi(LL a,LL b,LL p)
{
	LL res=1;
	while(b)
	{
		if(b&1) res=res*a%p;
		a=a*a%p;
		b>>=1;
	}
	return res%p;//这里取模  排除  b=0的特殊情况
}
int main(void)
{
	cin>>a>>b>>p;
	cout<<quick_mi(a,b,p);
	return 0;
}

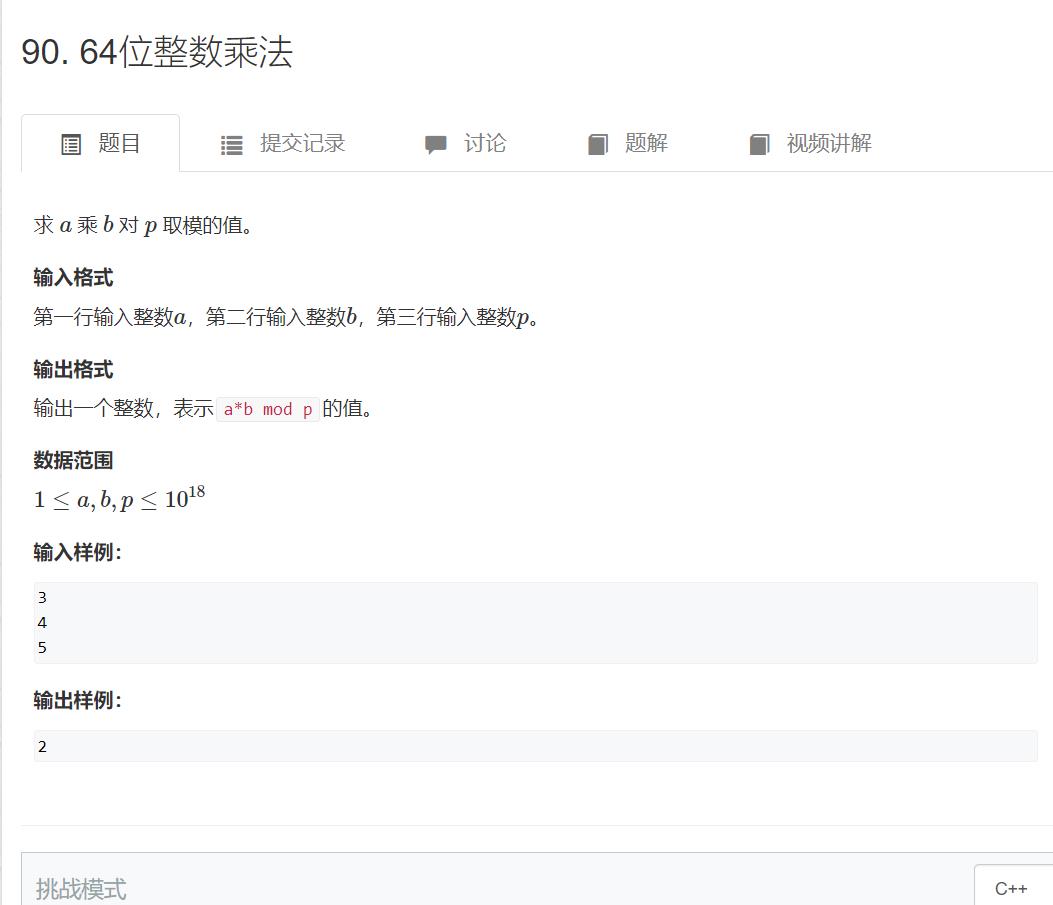
90. 64位整数乘法

在这里插入图片描述
题目地址

考察的知识点：还是二进制快速幂和上面的题的思路几乎一样，不过这里是加法而已。
因为 a*b 等于 b个a相加

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long int LL;
LL a,b,p;
LL f(LL a,LL b, LL p)
{
    LL res=0;
    while(b)
    {
        if(b&1) res=(res+a)%p;
        a=a*2%p;
        b=b>>1;
    }
    return res%p;
}
int main(void)
{
    cin>>a>>b>>p;
    cout<<f(a,b,p);
    return 0;
}

__128int写法

#include <bits/stdc++.h>
using namespace std;
 
void scan(__int128 &x)//输入
{
    x = 0;
    int f = 1;
    char ch;
    if((ch = getchar()) == '-') f = -f;
    else x = x*10 + ch-'0';
    while((ch = getchar()) >= '0' && ch <= '9')
        x = x*10 + ch-'0';
    x *= f;
}
void _print(__int128 x)
{
    if(x > 9) _print(x/10);
    putchar(x%10 + '0');
}
void print(__int128 x)//输出
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    _print(x);
}
 
int main()
{
    __int128 a,b,p;
    scan(a); scan(b); scan(p);
    print(a%p*b%p%p);
    return 0;
}

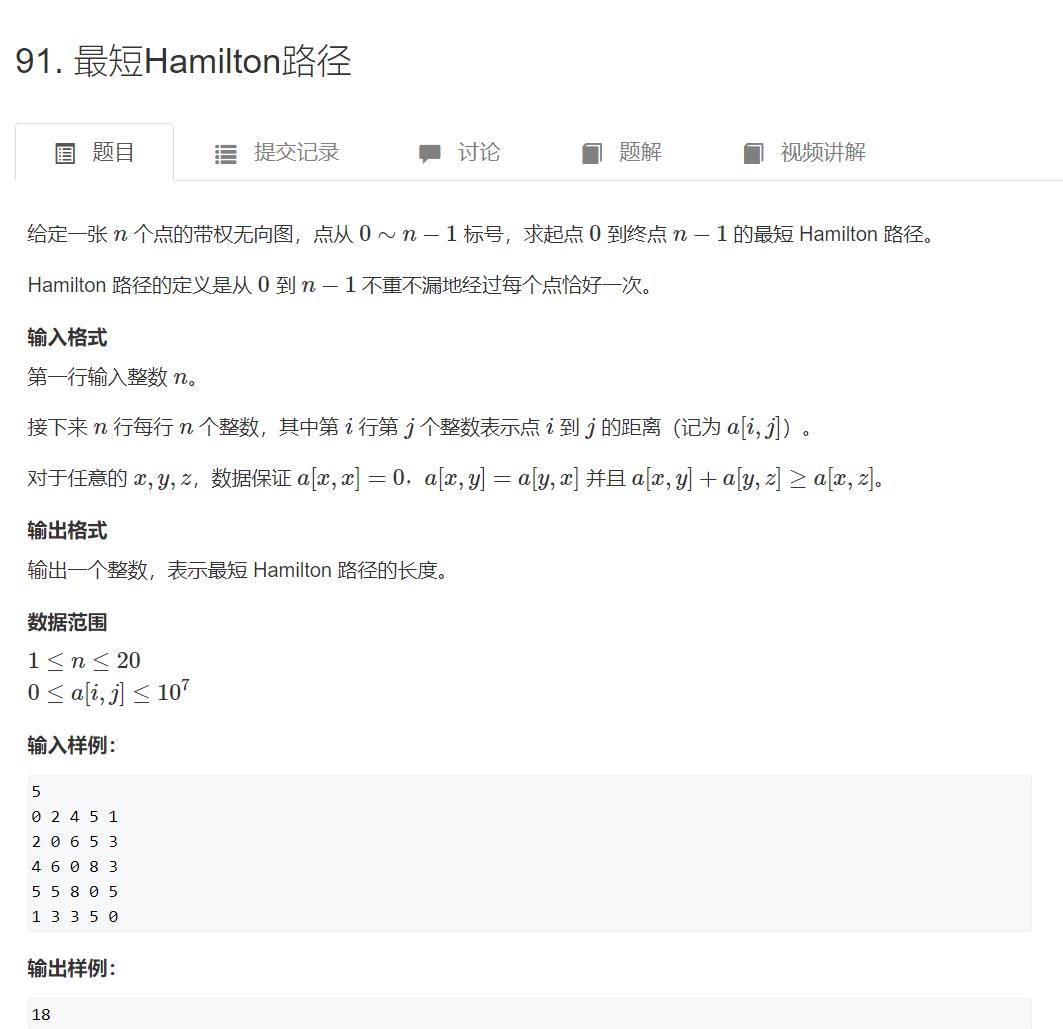
91. 最短Hamilton路径【二进制 / 状态压缩DP】

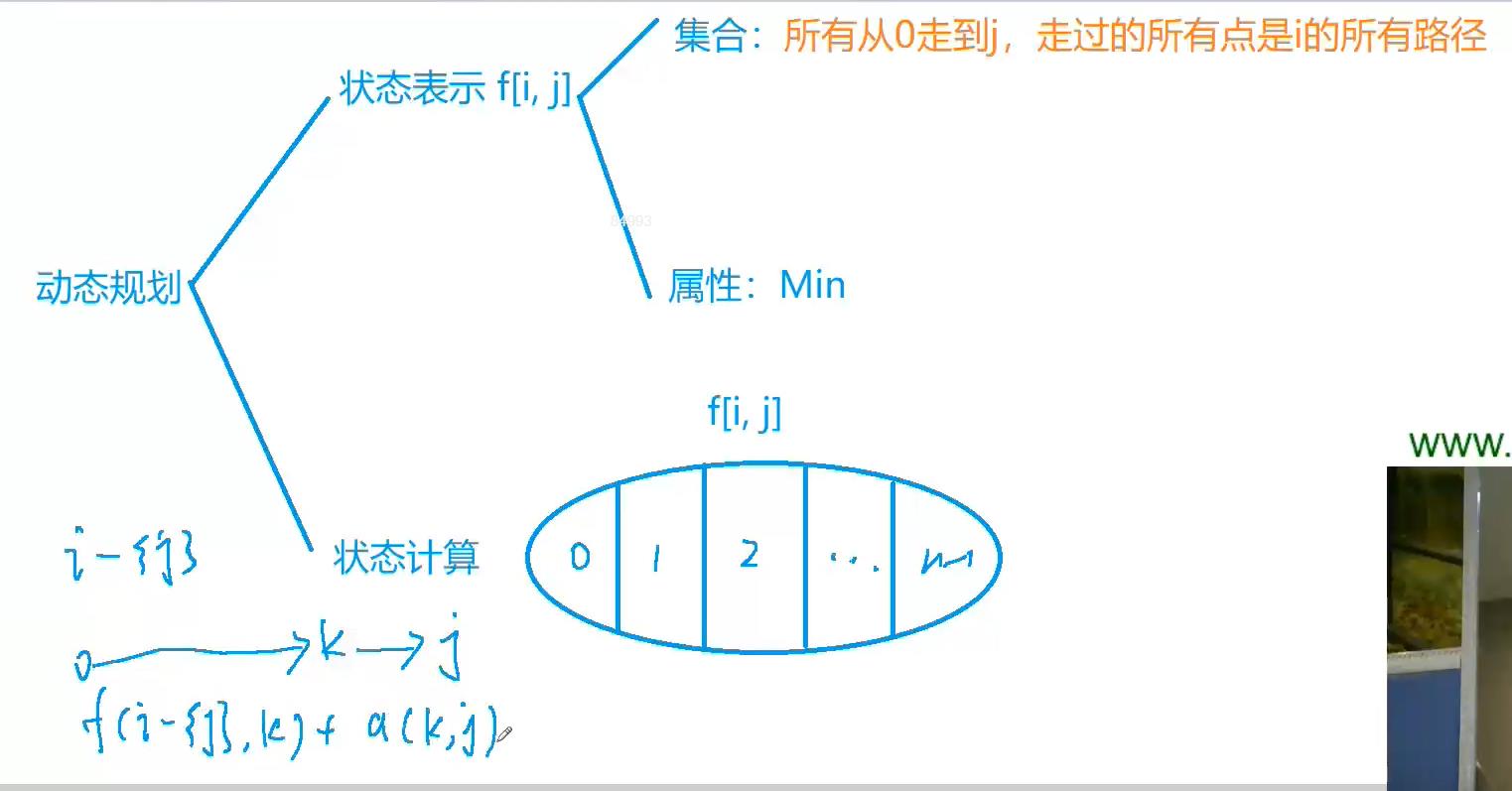
在这里插入图片描述
题目地址

在这里插入图片描述
状态表示f[i][j] i表示走过的点的集合，用二进制表示，1代表该点走过了 0代表还没有走过 j表示当前状态的终点的点

#include<cstdio>
#include<cstring> 
#include<iostream>
#include<algorithm>
using namespace std;
const int N=20,M=1<<20;
int f[M][N],w[N][N];
int n;
int main(void)
{
	int n; cin>>n;
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			cin>>w[i][j];
			
	memset(f,0x3f,sizeof f);
	f[1][0]=0;//当前在起点距离为0
	
	for(int i=0;i<(1<<n);i++)//走的点的集合 
	{
		for(int j=0;j<n;j++)
		{
			if(i>>j & 1 )//集合中含有j,是一种合法的状态。 因为j的含义是终点，所以i的集合中一定得有
			{
				for(int k=0;k<n;k++)//看一下上一个结点k 是否存在
				{
					if( (i-(1<<j))>>k & 1)//除掉j这个点，看剩余的集合中是否有k
					{
						f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);//从当前状态和从k转移到j的状态中选一个小的
					} 
				}
			}
		}
	}
	
	cout<<f[ (1<<n)-1][n-1]<<endl;
	return 0;
}

递推与递归

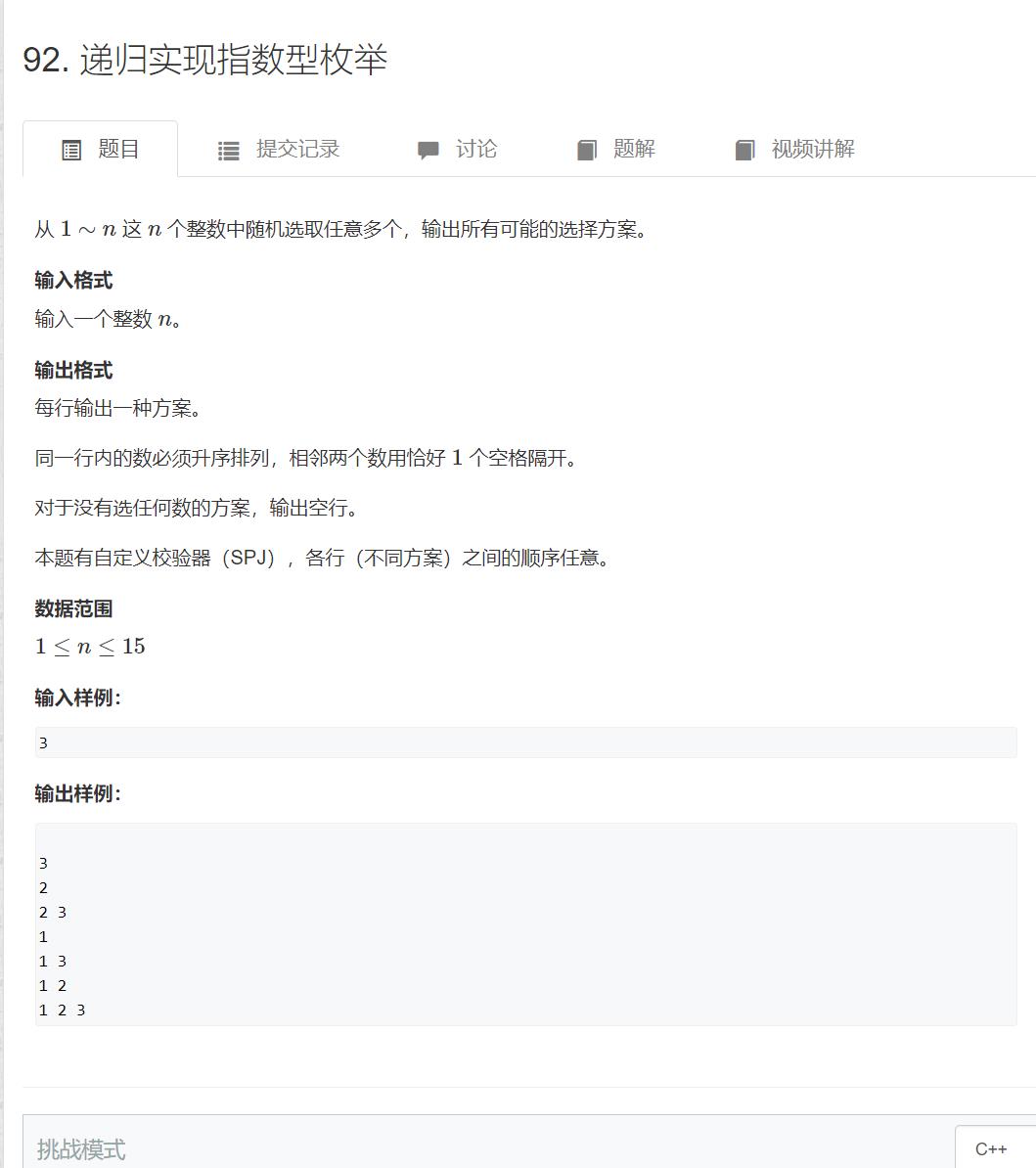
92. 递归实现指数型枚举

在这里插入图片描述
题目地址

#include<cstdio>
#include<iostream>
using namespace std;
int n;
int a[30];
void dfs(int index)
{
	if(index==n+1)
	{
		for(int i=1;i<=n;i++) 
		if(a[i]) cout<<i<<" ";
		cout<<endl;
		return ;
	}
	
	a[index]=1;
	dfs(index+1);
	a[index]=0;
	dfs(index+1);
}
int main(void)
{
	cin>>n;
	dfs(1);
	return 0;
}

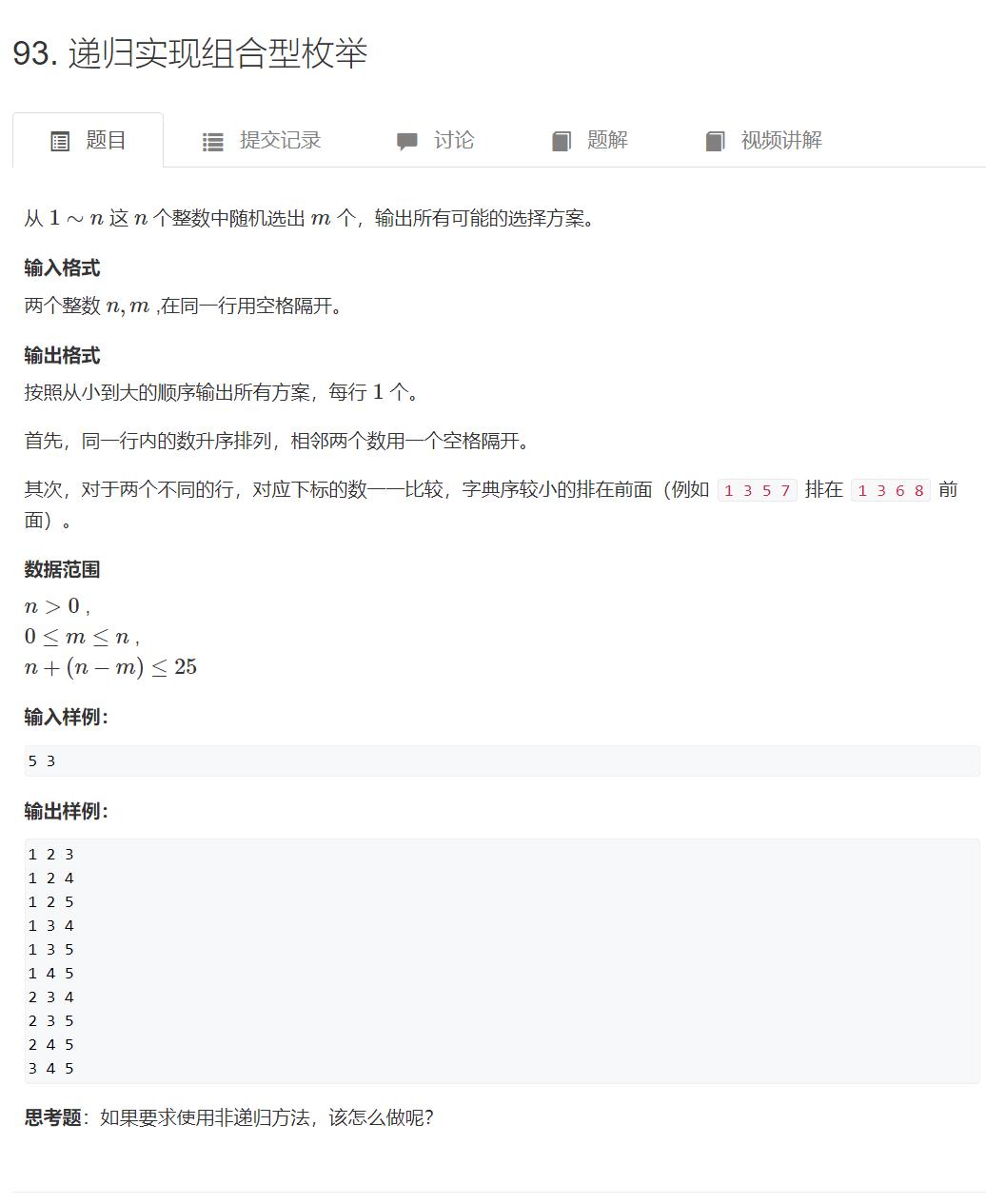
93. 递归实现组合型枚举

在这里插入图片描述
题目地址

#include<cstdio>
#include<iostream>
using namespace std;
int a[50];
bool st[50];
int n,k;
void dfs(int index,int start)
{
	if(index==k+1)
	{
		for(int i=1;i<=n;i++)
		if(st[i]) cout<<i<<" ";
		cout<<endl;
		return ;
	}
	for(int i=start;i<=n;i++)
	{
		if(!st[i])
		{
			st[i]=true;
			dfs(index+1,i);
			st[i]=false;
		}
	}
}
int main(void)
{
	cin>>n>>k;
	dfs(1,1);
	return 0;
}

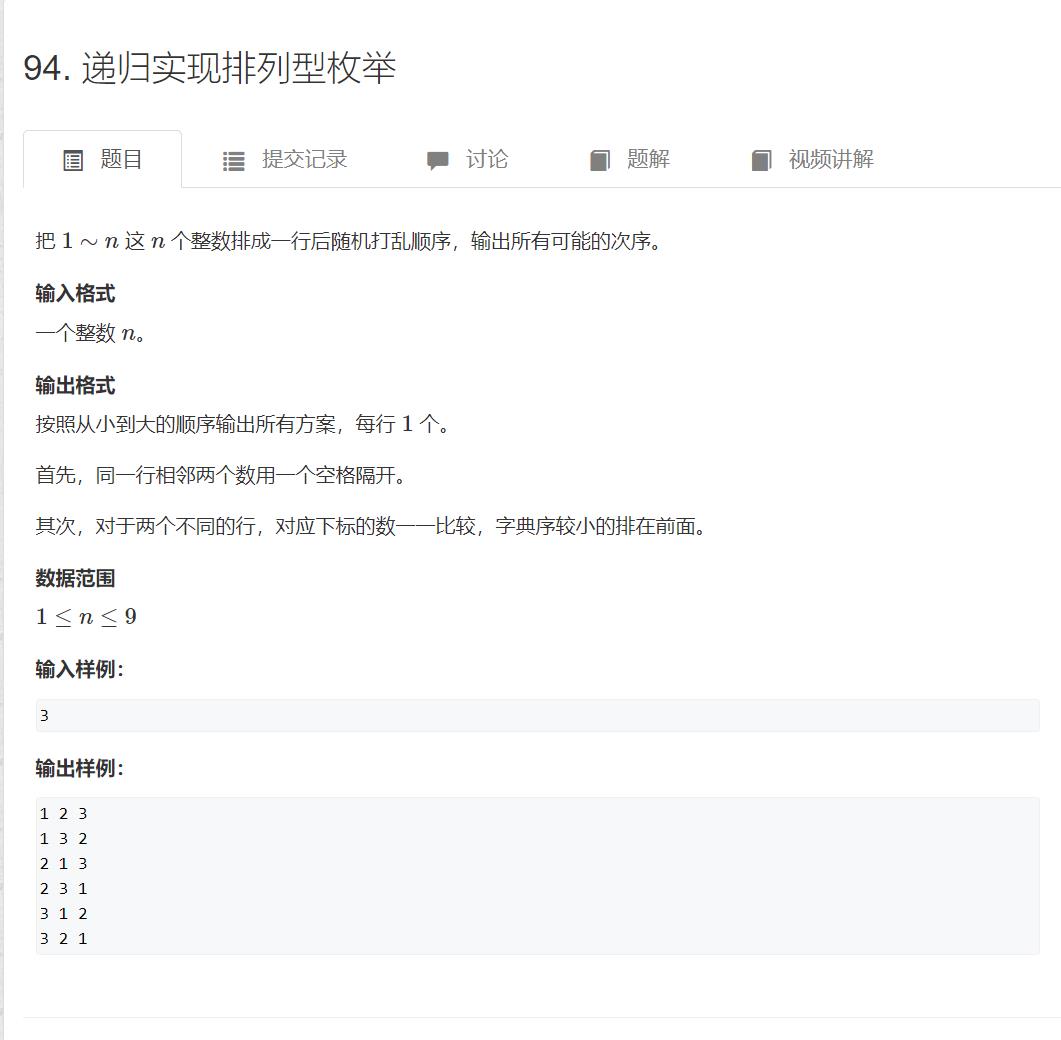
94. 递归实现排列型枚举

在这里插入图片描述
题目地址

#include<cstdio>
#include<iostream>
using namespace std;
int a[50];
bool st[50];
int n;
void dfs(int index)
{
	if(index==n+1)
	{
		for(int i=1;i<=n;i++) cout<<a[i]<<" ";
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++)
	{
		if(!st[i])
		{
			a[index]=i;
			st[i]=true;
			dfs(index+1);
			st[i]=false;
		}
	}
}
int main(void)
{
	cin>>n;
	dfs(1);
	return 0;
}