LeetCode 5. 最长回文子串

Posted 2021-06-26 数据结构和算法

想看更多算法题，可以扫描上方二维码关注我微信公众号“数据结构和算法”，截止到目前我已经在公众号中更新了500多道算法题，其中部分已经整理成了pdf文档，截止到目前总共有1000多页（并且还会不断的增加），可以在公众号中回复关键字“pdf”即可下载。

public String longestPalindrome(String s) {
    if (s.length() < 2)
        return s;
    int start = 0;
    int maxLen = 0;
    for (int i = 0; i < s.length() - 1; i++) {
        for (int j = i; j < s.length(); j++) {
            //截取所有子串，然后在逐个判断是否是回文的
            if (isPalindrome(s, i, j)) {
                if (maxLen < j - i + 1) {
                    start = i;
                    maxLen = j - i + 1;
                }
            }
        }
    }
    return s.substring(start, start + maxLen);
}

//判断是否是回文串
private boolean isPalindrome(String s, int start, int end) {
    while (start < end) {
        if (s.charAt(start++) != s.charAt(end--))
            return false;
    }
    return true;
}

public String longestPalindrome(String s) {
    if (s.length() < 2)
        return s;
    int start = 0;
    int maxLen = 0;
    for (int i = 0; i < s.length() - 1; i++) {
        for (int j = i; j < s.length(); j++) {
            //截取所有子串，如果截取的子串小于等于之前
            //遍历过的最大回文串，直接跳过。因为截取
            //的子串即使是回文串也不可能是最大的，所以
            //不需要判断
            if (j - i < maxLen)
                continue;
            if (isPalindrome(s, i, j)) {
                if (maxLen < j - i + 1) {
                    start = i;
                    maxLen = j - i + 1;
                }
            }
        }
    }
    return s.substring(start, start + maxLen);
}

//判断是否是回文串
private boolean isPalindrome(String s, int start, int end) {
    while (start < end) {
        if (s.charAt(start++) != s.charAt(end--))
            return false;
    }
    return true;
}

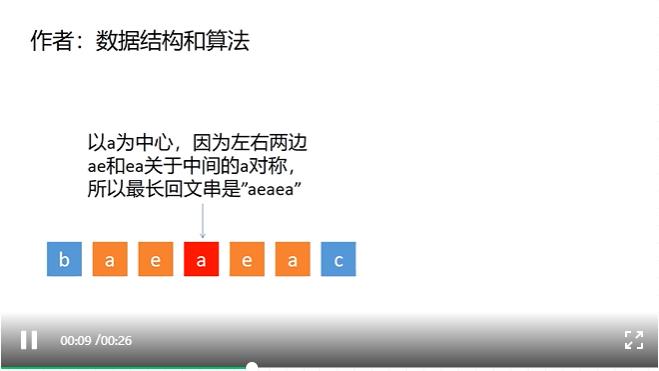
由于CSDN不支持视频，这里放了视频的连接

视频演示

String longestPalindrome(String s) {
    //边界条件判断
    if (s.length() < 2)
        return s;
    //start表示最长回文串开始的位置，
    //maxLen表示最长回文串的长度
    int start = 0, maxLen = 0;
    int length = s.length();
    for (int i = 0; i < length; ) {
        //如果剩余子串长度小于目前查找到的最长回文子串的长度，直接终止循环
        // （因为即使他是回文子串，也不是最长的，所以直接终止循环，不再判断）
        if (length - i <= maxLen / 2)
            break;
        int left = i, right = i;
        while (right < length - 1 && s.charAt(right + 1) == s.charAt(right))
            ++right; //过滤掉重复的
        //下次在判断的时候从重复的下一个字符开始判断
        i = right + 1;
        //然后往两边判断，找出回文子串的长度
        while (right < length - 1 && left > 0 && s.charAt(right + 1) == s.charAt(left - 1)) {
            ++right;
            --left;
        }
        //保留最长的
        if (right - left + 1 > maxLen) {
            start = left;
            maxLen = right - left + 1;
        }
    }
    //截取回文子串
    return s.substring(start, start + maxLen);
}

public static String longestPalindrome(String s) {
    //边界条件判断
    if (s.length() < 2)
        return s;
    //start表示最长回文串开始的位置，
    //maxLen表示最长回文串的长度
    int start = 0, maxLen = 1;
    int length = s.length();
    boolean[][] dp = new boolean[length][length];
    for (int right = 1; right < length; right++) {
        for (int left = 0; left < right; left++) {
            //如果两种字符不相同，肯定不能构成回文子串
            if (s.charAt(left) != s.charAt(right))
                continue;

            //下面是s.charAt(left)和s.charAt(right)两个
            //字符相同情况下的判断
            //如果只有一个字符，肯定是回文子串
            if (right == left) {
                dp[left][right] = true;
            } else if (right - left <= 2) {
                //类似于"aa"和"aba"，也是回文子串
                dp[left][right] = true;
            } else {
                //类似于"a******a"，要判断他是否是回文子串，只需要
                //判断"******"是否是回文子串即可
                dp[left][right] = dp[left + 1][right - 1];
            }
            //如果字符串从left到right是回文子串，只需要保存最长的即可
            if (dp[left][right] && right - left + 1 > maxLen) {
                maxLen = right - left + 1;
                start = left;
            }
        }
    }
    //截取最长的回文子串
    return s.substring(start, start + maxLen);
}